Journal of Geography  & Natural Disasters
Open Access

The Nonlinear Influence of Large Celestial Bodies on Earthquakes

Michael Nitsche^{* *}Correspondence: Michael Nitsche, Department of Mathematical Geology, Ateneo de Manila University, Quezon, Philippines, Email:

Author info »

References

1. Nitsche M. Triggering Earthquakes Fluctuations of The Planetary Gravitational Field and Nonlinear Interactions with Matter. Eart Envi Scie Res Rev. 5 (1):2022;1-18.

   [Crossref] [Google scholar]

2. Brack T, Zybach B, Balabdaoui F, Kaufmann S, Palmegiano F, Tomasina JC, et,al. Dynamic measurement of gravitational coupling between resonating beams in the hertz regime. Nat Phys. 2022 11:1-6.

   [Crossref] [Google scholar]

3. Kennedy M, Vidale JE, Parker MG. Earthquakes and the moon: syzygy predictions fail the test. Seismol Res Lett.2004; 75(5):607-612.

   [Crossref] [Google scholar]

4. Kasahara J. Tides, earthquakes, and volcanoes. Scie. 2002; 297(5580):348-349.

   [Crossref] [Google scholar]

5. Métivier L, de Viron O, Conrad CP, Renault S, Diament M, Patau G. Evidence of earthquake triggering by the solid earth tides. Earth Planet Sci Lett.2009; 278(3-4):370-375.

   [Crossref] [Google scholar]

6. Kolvankar VG. Sun, moon and earthquakes. New Concepts in Global Tectonics Newsletter. 2011; 60:50-66.

   [Google scholar]

7. Cochran ES, Vidale JE, Tanaka S. Earth tides can trigger shallow thrust fault earthquakes. Scie. 2004;306(5699):1164-1166.

   [Crossref] [Google scholar]

8. Wilhelm H, Zürn W, Wenzel HG. Tidal phenomena. Lecture Notes in Earth Sciences, Berlin Springer Verlag. 1997;66

   [Google scholar]

9. Nitsche ME. Are the Stabilizing and Destabilizing Influences of the Planetary Gravitational Field on the Structural Formation of Complex Systems Real. InTriggering of Earthquakes–Lecture on the 2002 Annual Conference of the International Association for Mathematical Geology 2001.

   [Crossref] [Google scholar]

10. Nitsche ME. The non-linear interaction of the planetary gravitational field on earthquakes. IAMG. 2001:7-12.

    [Crossref] [Google scholar]

11. Triggering Earthquakes Fluctuations of The Planetary Gravitational Field and Nonlinear Interactions with Matter
12. Nitsche M. Fluctuations of the planetary gravitational field and nonlinear interactions with matter as an element of artificial intelligence. J Robot Auto Res, 3 (1), 124-130. Michael Nitsche, Bachstraße. 2022;13:72415.

    [Google scholar]

13. Nitsche M. Fluctuations of the planetary gravitational field and nonlinear interactions with matter.

    [Crossref] [Google scholar]

About the Study

A new study on the nonlinear interaction of the fluctuating planetary gravitational field with the lithosphere suggests that not only the directly acting gravitational forces are of influence, but mainly higher harmonics of the celestial bodies considered as oscillators on large scales [1]. In the meantime, resonances caused by fluctuating gravity can also be detected on small scales in the laboratory [2]. Gravity is a force that acts both on large scales, the planetary system, and on small scales, on the micro scale of atoms. The kinematics of the planets correspond to oscillators that have been stable and have been able to exert their effects over billions of years of evolution. The gravitational forces are weak and sensually only in the coupling of sun and moon in the tides directly noticeable. As in nonlinear optics, the special effects of the fluctuating gravitational field become visible only in the harmonics. A correlation function constructed to indicate the change in probabilities for stable (harmonic) and unstable (disharmonic) states is also applied to earthquake triggering.

Tidal stresses are very small, so there is still a lot of debate about whether they can trigger an earthquake at all. Several studies have found no correlation between tides and earthquake occurrence, e.g. Kennedy [3]. Other studies report small positive correlations, e.g. Kasahara [4]. Some recent research by Metivier suggests evidence that tidal- induced uplift may reduce the normal stresses that hold faults together [5].

Previous studies related to the triggering of earthquakes do not take into account the gravitational interactions of the planets e.g. [6-8]. A correlation function [1] is a Fourier series expansion of a periodic process and can be optimized both in its order and in its frequencies for the respective problem. It has the function of a high pass filter.

Hi, j is the correlation of two celestial bodies; Σ is the angle between two celestial bodies; ak are the 12 coefficients of the Fourier series repeated N times; N is the order of the correlation function. The coefficients ak were obtained from a Fourier transform describing the change in probability for stable and unstable processes, respectively.

This new research method was applied to an initial study of 41 of the strongest earthquakes between 1900 and 2000 and first published as Lecture on the 10th conference on synergetics and complexity research: “Self. Organization in Psychology, Psychiatry and Social Sciences” 6th-8th June 2002 conference centre Bildungszentrum Kloster Seeon (Bavaria, Germany) [9]. The result shows the density function Figure 1.

Figure 1: 1^st order density function Σ Hi, j with N=1. Sun, Moon, Jupiter, Uranus and Neptune were correlated. The significance is very high 0.03% (99.97% of the 10 000 control groups are more harmonic).

Monte Carlo simulation was used to calculate the density function. 10 000 groups of 41 events each were randomly selected in the period from 1900 to the end of 2000. Further research on the 41 earthquakes [1].

Other groups of earthquakes were presented at various international congresses, including International Association for Mathematical Geology IAMG 2003 Portsmouth, UK; September 7-12, 2003 [10] and EGS-AGU-EUG; Joint Assembly Nice, France, April 25-30, 2004 [11].

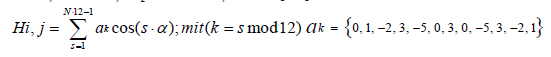
The method was extended in 2021 by investigations of the whole period before and after an earthquake. An estimation of the suitability of this method as an element for earthquake forecasting was also carried out (585 earthquakes [12]).

If only the absolute value of the correlation function (proportional to the energy) is considered, the following course before and after the earthquake is obtained in Tables 1 and 2.

Examination of the Sun, Moon, Jupiter, Saturn and IC alone shows that something like 6% of the 588 earthquakes may be triggered by these celestial bodies. These results refer to the superposition of all correlations.

Looking at this more closely, we can see that individual correlations produce a pattern that could lend itself as one element (among many others) to predicting earthquakes [13].

The correlation matrix Hi, j shows a specific pattern of probability for instability for the 588 earthquakes Tables 3 and 4.

Conclusion

The whole matrix is not significantly unstable. 85.8% of the 3000 control groups show more stability. However, 9 correlations show significant instability against no correlation shows significant stability. This pattern of instability, in conjunction with other elements of the correlation function Hi, j (e.g.1st derivative of the function), may appear suitable to be incorporated as an element in an AI. However, further investigations are necessary for this purpose. The computer program can be downloaded here for free.