Onsager’s theory is based on three assumptions [1,2]: i) The probability distribution function for the fluctuations of thermodynamic quantities (Temperature, pressure, degree of advancement of a chemical reaction etc.) is a Maxwellian ii) Fluctuations decay according to a linear law and iii) The principle of the detailed balance (or the microscopic reversibility) is satisfied. Onsager showed the equivalence of the assumptions i)-iii) with the equations

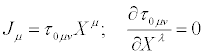(1)

Where 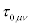are the transport coefficients 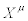and and 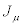denote the thermo- dynamic forces and the conjugate fluxes, respectively. Assumption iii) allows deriving the reciprocity relations 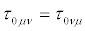. Note that in Equation. (1), as well asin the sequel, the summation convention on the repeated indexes is understood. The Onsager theory of fluctuations starts from the Einstein formula linking the probability of a fluctuation, W, with the entropy change, ΔS, associated with the fluctuations from the state of equilibrium

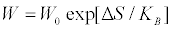(2)

In Equation. (2), K_B is the Bolzmann constant and W₀ is a normalization constant, which ensures that the sum of all probabilities equals to one. Prigogine generalized Equation. (2), which applies only to adiabatic or isothermal transformations, by introducing the entropy production due to fluctuations. Denoting by 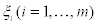the m deviations of the thermodynamic quantities from their equilibrium value, Prigogine proposed that the probability distribution of finding a state in which the values 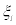ilie between 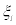and 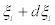is given by 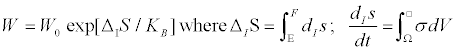[3]

(3)

dV is a (spatial) volume element of the system, and the integration is over the entire space Ω occupied by the system in question. E and F indicate the equilibrium state and the state to which a fluctuation has driven the system, respectively. Note that this probability distribution remains unaltered for flux-force transformations leaving invariant the entropy production. Concrete examples of chemical reactions, equivalent from the thermodynamic point of view, have also been analyzed in literature. As an example, among these, we choose the simplest of all. Let us consider, for example, a chemical system in which

a) two isomerisations A→B and B→C take place [3]. From the macroscopic point of view, the chemical changes could be equally well described by the

b) two isomerisations A→C and B→C. It can be checked that, under a linear transformation of the thermodynamic forces (i.e., in this case, a linear transformation of the chemical affinities) the entropy productions, corresponding to the two chemical reactions a) and b), are equal. Indeed, the corresponding affinities of the reactions a) rea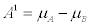d: and 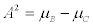with Aⁱ and 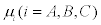denoting the affinities and the chemical potentials, respectively. The change per unit time of the mole numbers is given by

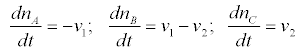(4)

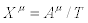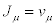With v_i (i=1,2) denoting the chemical reaction rates. In this case the thermodynamic forces and the flows are the chemical affinities (over temperature) and the chemical reaction rates, respectively i.e., and . Hence, the corresponding entropy production reads 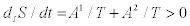. The affinities corresponding to reactions b) are related to the old ones by

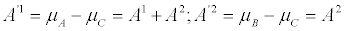(5)

By taking into account that

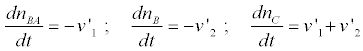(6)

we get

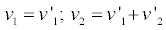(7)

Where the invariance of the entropy production is manifestly shown. Indeed,

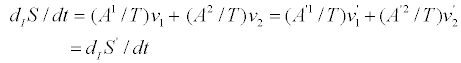(8)

Or 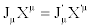(where the Einstein summation convention on the repeated indexes is adopted). On the basis of the above observations, Th. De Donder and I. Prigogine formulated, for the first time, the concept of equivalent systems from the thermodynamical point of view. For Th. De Donder and I. Prigogine, thermodynamic systems are thermodynamically equivalent if, under transformation of fluxes and forces, the bilinear form of the entropy production remains unaltered, i.e., 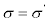. [4].

However, the condition of the invariance of the entropy production is not sufficient to ensure the equivalence character of the two descriptions 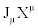and 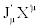. Indeed, we can convince ourselves that there exists a large class of transformations such that, even though they leave unaltered the expression of the entropy production, they may lead to certain paradoxes to which Verschaffelt has called attention [5,6]. This obstacle can be overcome if one takes into account one of the most fundamental and general theorems valid in thermodynamics of irreversible processes: the Universal Criterion of Evolution. In general, Glansdorff and Prigogine have shown that: For time-independent boundary conditions, a thermodynamic system, even in strong nonequilibrium conditions, relaxes to a stable stationary state in such a way that the following Universal Criterion of Evolution is satisfied [7,8].

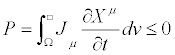(9)

Here, Ω is the volume occupied by the system and dV the volumeelement, respectively. In addition

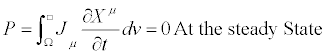(10)

Quantity 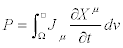may be referred to as the Glansdorff- Prigogine dissipative quantity.

Let us check the validity of this theorem by considering two, very simple, examples. Let us consider, for instance, a closed system containing m components (i=1,…,m) among which chemical reactions are possible. The temperature, T, and the pressure, P are supposed to be constant in time. The chance in the number of moles n_i, of component i, is

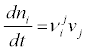(11)

With 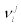denoting the stoichiometric coefficients. By multiplying both members of Equation. (11) by the time derivative of the chemical potential of component i, we get

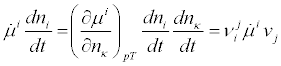(12)

By taking into account the De Donder law between the affinities Aⁱ and the chemical potentials i.e., 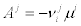, we finally get

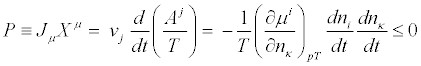(13)

Where the negative sign of the term on the right-hand side is due to the second law of thermodynamics. Hence, the Glansdorff- Prigogine dissipative quantity P is always negative, and it vanishes at the stationary state. As a second example, we analyze the case of heat conduction in non-expanding solid. In this case the thermodynamic forces and the conjugate flows are the (three) components of the gradient of the inverse of the temperature, 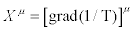and the (three) components of the heat flow, 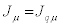(with i=1,2,3), respectively. Hence,

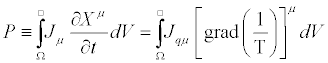(14)

With partial integration, and by taking into account the energy law

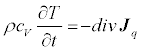(15)

after simple calculations, we get

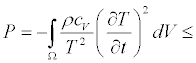(16)

With P=0 at the steady state. In Equations (15) and (16), ρ and c_V are the mass density and the specific heat at volume constant, respectively. By summarizing, without using neither the Onsager reciprocal relations nor the assumption that the phenomenological coefficients (or linear phenomenological laws) are constant, the dissipative quantity P is always a negative quantity. This quantity vanishes at the stationary state. In the two above-mentioned examples, the thermodynamic forces are the chemical affinities (over temperature) and the gradient of the inverse of temperature, respectively. However, we could have adopted a different choice of the thermodynamic forces. If we analyze, for instance, the case of heat conduction in non-expanding solid, where chemical reactions take place simultaneously, we can choose as thermodynamic forces a combination of the (dimensionless) chemical affinities (over temperature) and the (dimensionless) gradient of the inverse of temperature. Clearly, this representation is thermodynamically equivalent to the one where the thermodynamic forces are simply the chemical affinities (over temperature) and the gradient of the inverse of temperature, only if the transformation between the thermodynamic forces preserves the negative sign of the quantity P. In particular, the two equations for the stationary states [the Equation. (10) and its transformed] must admit the same solutions. In other words, to ensure the equivalent character of the two descriptions, 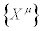and 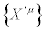, it is not sufficient to require that 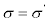, but we should require that also the Glansdorff-Prigogine dissipative quantity remains invariant under transformation of the thermodynamic forces 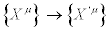. Magnetically confined Tokamak plasmas are a typical example of thermodynamic systems, out of Onsager’s region, where the Glansdorff-Prigogine dissipative quantity remains invariant under transformation of the thermodynamic forces [9].

In the light of the above, we formulate the following principle: Two systems are equivalent from the thermodynamic point of view if, under transformation 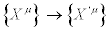, we have 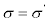and 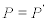[11]. This kind of transformations may be referred to as the Thermodynamic Coordinate Transformations (TCT). The aim of this work is to derive from the admissible thermodynamic forces, the most general class of transformations (TCT) so that two thermodynamic systems are equivalent from the thermodynamic point of view. We shall prove that under TCT, σ and Premain invariant and, in addition, the reciprocity relations of the transformed transport matrix are preserved.

The thermodynamic equivalence principle leads, naturally, to the following Thermodynamic Covariance Principle (TCP): The nonlinear closure equations (i.e., the flux-force relations valid out of Onsager’s region) must be covariant under TCT. The essence of the TCP is the following. The equivalent character of two representations is warranted if, and only if, the fundamental thermodynamic equations are covariant under TCT. In fact, a covariant formulation guarantees the writing of the fundamental laws of thermodynamics (for instance, the flux-force closure equations) in a form that is manifestly invariant under trans- formation between the admissible thermodynamic forces. This is the correct mathematical formalism to ensure the equivalence between two different representations. Note that the TCP is trivially satisfied by the closure equations valid in the Onsager region. It is worthwhile mentioning that the linear version of the TCT (see the next section) is actually largely used in a wide variety of thermodynamic processes ranging from non-equilibrium chemical reactions to transport processes in Tokamak plasmas (see, for examples, the papers cited in the book [10]). To the author’s knowledge, the validity of the thermodynamic covariance principle has been verified empirically without exception in physics until now.

Consider a thermodynamic system driven out of equilibrium by a set of n independent thermodynamic forces 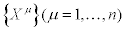. It is also assumed that the system is submitted to time-independent boundary conditions. The set of conjugate flows, 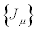, is coupled to the thermodynamic forces through the relation

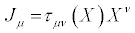(17)

Where the transport coefficients, 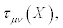may depend on the thermodynamic forces. The symmetric piece of 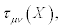is denoted with 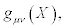and the skew- symmetric piece as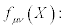

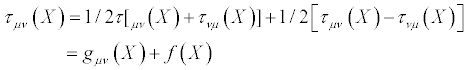(18)

Where

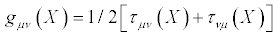(19)

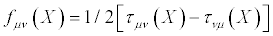20)

It is assumed that 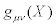is a positive definite matrix. For the sake of conciseness, in the sequel we drop the symbol (X ) in 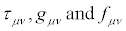, being implicitly understood that these matrices may depend on the thermodynamic forces. With the elements of the transport coefficients two objects are constructed: operators, which may act on thermodynamic tensorial objects and thermodynamic tensorial objects, which under coordinate (forces) transformations, obey to well specified transformation rules.

Two operators are introduced, the entropy production operator σ (X)and the dissipative quantity operator 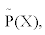, acting on the thermodynamic forces in the following manner

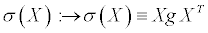
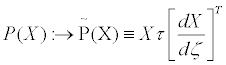(21)

In Equations (21), the transport coefficients are then considered as elements of the two n x n matrices, τ and g. Symbol T stands for the transpose of the matrix. The positive definiteness of the matrix g_μν ensures the validity of the second principle of thermodynamics: σ ≥ 0 . These matrices multiply the thermodynamic forces X expressed as n x1 column matrices. We already anticipate that parameter defined in Equation. (33), is invariant under the thermodynamic coordinate transformations.

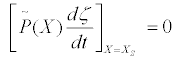(22)

Thermodynamic states X_S such that are referred to as steady states. Of course, the steady states should be invariant expressions under the thermodynamic coordinate transformations. Equations (21) should not be interpreted as the metric tensor g_μν , which acts on the coordinates. The metric tensor acts only on elements of the tangent space (like dX^μ see the forthcoming sub-section) or on the thermodynamic tensorial objects.

In the previous section we stated that two systems are equivalent from the thermodynamic point of view if, under TCT, 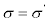and 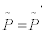remain unaltered. In mathematical terms, this implies:

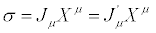(23)

This condition and the condition that also the dissipative quantity [cf. Equations (21)] must be an invariant expression, require that the transformed thermodynamic forces and flows satisfy the relation

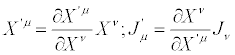(24)

These transformations may be referred to as Thermodynamic Coordinate Transformations (TCT). The expression of entropy production becomes accordingly

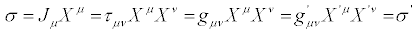(25)

From Equations (24) and (25) we derive

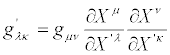(26)

Moreover, inserting Equations (24) and Equation. (26) into relation 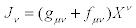, we obtain

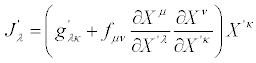(27)

or

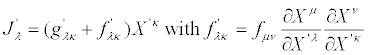(28)

Hence, the transport coefficients transform like a thermodynamic tensor of second order¹. ¹We may qualify as thermodynamic tensor or, simply thermo-tensor, (taken as a single noun) a set of quantities where only transformations Equations (24) are involved. This is in order to qualify as tensor, a set of quantities, which satisfies certain laws of transformation when the coordinates undergo a general transformation. Consequently every tensor is a thermodynamic tensor but the converse is not true.

It is easily checked that transformations (24) preserve the validity of the reciprocal relations for transport coefficients i.e., if 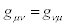then 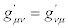(and, if 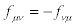then )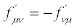

By direct inspection, it is easy to verify that the general solutions of equations (24) are

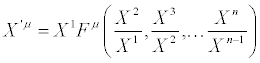(29)

where F^μ are arbitrary functions of variables 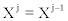with (j=2,… ,n). Equation. (29) is the most general class of transformations expressing the equivalent character of two descriptions 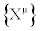and 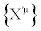. Hence, the TCT may be highly nonlinear coordinate transformations but, in the Onsager region, we may (or we must) require that they have to reduce to

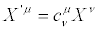(30)

where 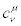are constant coefficients (i.e., independent of the thermodynamic forces). The linear and homogeneous transformations (30) are largely used in literature because, besides their simplicity, they are nonsingular transformations. We note that from Equation. (24), the following important identities are derived

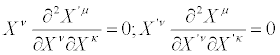(31)

Moreover

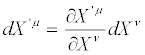
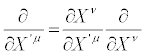(32)

i.e., dX^μ and ∂ / ∂X^μ transform like a thermodynamic contravariant and a thermodynamic covariant vector, respectively. According to Equation. (32), thermodynamic vectors dX^μ define the tangent spaceto Ts. It also follows that the operator P(X), i.e. the dissipation quantity, and in particular the definition of steady states, are invariant under TCT. Parameter ς , defined as

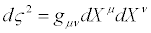(33)

is a scalar under TCT. The operator O

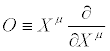(34)

is also invariant under TCT. This operator plays an important role in the formalism [11]. We may now enunciate the Thermodynamic Covariance Principle (TCP) :All thermodynamic equations involving the thermodynamic forces and flows (e.g., the closure equations) should be covariant under TCT.

From this principle, it is possible to obtain the (nonlinear) closure equations by truncating the equations (obtained, for instance, by kinetic theory) relating the thermodynamic forces with the conjugate flows in such a way that the resulting expressions satisfy the TCP. A concrete example is briefly mentioned in the Conclusions.

If one requires only the entropy production to be invariant, but does not impose the auxiliary condition that he Glansdorff-Prigogine dissipative quantity should also be invariant under TCT, there exists the larger class of transformations leading to the phenomenological coefficients scheme, for which the reciprocal relations are not valid [12,13]. As rightly pointed out by Verschaffelt and Davies,”to impose that only the entropy production must be invariant under flux-force transformations may lead to paradoxes or inconsistencies” [5,6]. We must also keep in mind that the original form of the entropy production, as derived from the various balance equations, is such that the Onsager relations are valid. The correct way to overcome this impasse is to require that both the entropy production and the Glansdorff-Prigogine dissipative quantity remain unaltered under TCT.

The Nonlinear theory, the Thermodynamic Field Theory (TFT), reported in [11], is based on the validity of the Thermodynamic Covariance Principle. This assumption allows truncating, at the lowest order, the (highly nonlinear) equations relating the thermodynamic forces with the conjugate flows. For example, in the case of magnetically confined Tokamak-plasmas, these relations are obtained by kinetic theory and are expressed by highly nonlinear integral equations [14]. In this specific case, the generalized frictions are the thermodynamic forces whereas the conjugate flows are the Hermitian moments [10]. The Hermitian moments are linked to the deviation of the distribution function from the (local) Maxwellian, whereas the generalized frictions are linked to the collision term. According to the TCP, these integral equations may be truncated in such a way that the resulting expressions are covariant under TCT. The derived closure equations have been recently used for estimating the electron and ion losses (particle and heat losses) as well as the electron and ion distributions functions [9,12]. The theoretical predictions are fairly in line with the preliminary experimental data obtained for FTU-plasmas (FTU= FrascatiTokamak Upgrade).

We conclude by mentioning that attempts to derive a generally covariant thermodynamic field theory (GTFT) can be found in refs [15-17]. In References [15,16], the general covariance has been assumed to be valid for general transformations in the space of thermodynamic configurations, whereas in [17] it is argued that the entropy production rate should be invariant under general spatial coordinate transformations (in [17] the invariance of the Prigogine- Glansdorff dissipation is not satisfied). However, it is a matter of fact that a generally covariant thermodynamic theory, which is based solely on the invariance of the entropy production is, in reality, respected only by a very limited class of thermodynamic processes. As mentioned, a correct thermodynamic formalism must satisfy the TCP.