Journal of Tourism & Hospitality
Open Access
ISSN: 2167-0269
ISSN: 2167-0269
Research Article - (2015) Volume 4, Issue 5
The demand for most recreation activities is weather dependent. In this paper we study this weather dependence for a high number of recreation sites across the Austrian Province of Styria. We divide the recreation sites into three categories: bathing, outdoor and indoor. For the three categories of facilities we can find different patterns of weather dependence which go along with findings in the existing literature. While demand for bathing sites increases with increasing temperature, the demand for outdoor sites increases up to a threshold temperature and decreases afterwards. Finally, we find that demand for indoor activities is negatively related to temperature. In addition to the illustration of the weather dependence, we use a simple warehouse model to demonstrate for three examples to what extend managers of recreation site could profit from the knowledge of weather dependence of the demand.
<Keywords: Weather dependence, Recreation, Economic value of weather forecasts
Besides calendric effects like holidays, weekdays or special events, a major factor in the variability of attendance in recreation sites is the actual weather condition. Whereas for outdoor recreation sites “nice” weather would imply a higher number of visitors, indoor recreation sites will be used as alternatives on days with bad weather. This will lead to a different weather dependent demand function depending on the type of activity.
The main motivation for this paper was to investigate the above mentioned demand function for a high number of different recreation sites and to investigate if there exists common patterns for different types of dependence structures. In a second step we try to estimate the economic value of forecasts that arises from an improved estimation of demand.
A further motivation for the collection of the weather dependence of recreation activities comes from touristic demand research. In the last few years there emerged some contributions that analyse the impact of weather on touristic demand [1]. For example examine the changes to the travel routes, the timing and the activity participation of international tourists in New Zealand. In addition [2], quantifies the impact of weather parameters on the participation in a scenic flight operation and a visitor center in the township of Franz Josef, both in New Zealand [3,4]. However investigate the effects of weather on the behaviour in theme parks. How the spatio-temporal behaviour of tourists is influenced by weather conditions is analysed by the use of GPS and GIS tools [5].
That tourists in urban destinations are quite weather resilient is pointed out for Hong Kong [6]. An investigation of tourist behaviour for a region comparable to ours is provided [7]. It shows for the whole of Austria that the relationship between touristic demand and temperature follows the form of an inverted u-shaped curve. The impact of the risk of severe weather events on tourism investigate the weather sensitivity of visitors on two lidos in the city of Zurich [8,9]. The weather sensitivity is then used to simulate climate change scenarios. However, none of these papers provides an economic value for their forecast. We therefore believe that we can make thereby a valuable contribution to this branch of literature.
Quite often climate indices are used to identify the dependence between touristic demand and climate variables. The most popular climate index is the TCI [10]. Further indices are developed by Morgan et al. [11] where a beach climate index is developed and where an index is developed which takes into account different aspects of weather (thermal, physical and aesthetical) [12]. Finally, they are consider the weather preferences of tourists for different types (beach, urban and mountain) of activities [13,14]. The results of the above mentioned studies are based on expert knowledge and surveys. Since tourists are mainly participating in recreation activities, the demand pattern for different recreational activities can help in the development of climate indices. Climate indices can be used subsequently to estimate the weather respectively climate risk of the tourism industry, a concept especially valuable for investment decisions, since it is derived from indicators widely used in the financial sector [15-17]. However investigate the thermal perceptions of beach users by questionnaire.
In the literature there are several studies that consider the relation between demand and weather conditions [18]. For example investigate the link between number of cyclists and weather condition in a recreation site near Vienna. The connection between weather and the number of cyclists is also considered for Montreal [19], Washington DC [20], Netherlands [21] and Auckland [22]. While the first three papers consider nonlinear relationship between weather and number of cyclists, the fourth considers a linear model. Analyse the visitors of the Danube Flood Plains National Park near Vienna and discuss the necessity to predict visitors for various recreational areas [23]. Discuss the necessity to monitor the access to parks and conclude that weather has a substantial impact on the number of visitors and the traffic caused [24]. Analyse the recreational use of park sites in urban areas of Sweden by methods of structural interviews and a combination of mean radiant temperature and park visitors [25]. They document a positive relation between thermal comfort and park use. Consider the impact of weather on golf participation in the greater Toronto area [26]. Investigate the influence of weather conditions on hiking [27]. Consider the influence of weather variables on the number of daily visitors in ski areas [28-30]. A number of papers investigate the impact of climate change on ski tourism [31-35].
The papers cited above concentrate on outdoor activities. In this paper we have considered two additional types of activities, namely bathing and indoor activities. Furthermore, we consider a large number of sites. The use of different sites and activities has the advantage that one can search for general patterns in the considered categories. In addition, one can investigate how stable these patterns are over different sites. Analyse the seasonal fluctuations of tourists in Australia and mention that the forecasting values can be improved substantially by the inclusion of climate variables [36]. However, they provide no estimate for the economic value of this improvement. Furthermore, there are some contributions that.
Indicate that their work is connected with recreation area management, but don’t give an in-depth description of the applicability of their results [18]. Nevertheless this motivated us to shed some light on the economic value on weather driven demand forecasts. Therefore, we have included a small hypothetical example related to the management of perishable goods on a recreation site (e.g., in a food booth). Managers of recreation sites need to forecast future demand in order to hold the optimal number of goods on stock. If the stock level is too low, the recreation site may face opportunity costs since customers will have to be rejected. In the opposite case, the recreation site will face costs from the goods depreciated quality. For this example we have used a simple probabilistic warehouse model, inspired an economic value to our weather based demand predictions [37].
For a given recreation site accurate weather data might not be available. So it is interesting to investigate the effect of less accurate data on the value of the forecast. To simulate less accurate data we also included a model where the precision of the used weather data was reduced.
The estimation of the economic value of forecasts is not a new concept. For example [38], use a 2 × 2 profit loss model to discuss the economic value of weather forecasts. Economic evaluation of weather forecasts in 2 × 2 contingency tables is further done [37-40]. At present a method to estimate the economic value of weather forecasts for Customer-Relationship-Management (CRM) decision making problems in leisure industries in South Korea [41]. The forecast value arises from the customer’s satisfaction as a consequence of the decisions taken by the user of the forecast. Here, one should note that the cited papers do not contain any demand forecasts regarding the evaluation of the weather forecasts.
To carry out a WEDDA (Weather Driven Demand Analysis) for recreation demand, we contacted several recreation sites in the Austrian province of Styria. We obtained daily attendance data from 63 recreation sites. As daily data of visitors are considered to be quite sensitive business data to any firm, we promised the sites anonymity with respect to our analysis. The length of the data ranges from one season up to several years. We divided the recreational facilities into 3 categories: Bathing (31 sites), outdoor activities (hiking, parks and zoos) (13 sites) and indoor activities (museums and indoor sports) (19 sites).
For our WEDDA we only considered days with at least 1 visitor, so our models explain the attendance level given that at least one visitor is present. Furthermore, several sites have days with special events like traditional folk events, special guided tours or days of free entrance. These events can lead to an outlier in the number of visitors. Since we had no information on the timing of these events, we tried to remove outliers from the dataset. To detect possible outliers we first run a log linear model (compare section 3.1) with year, weekday and month as independent variables and deleted points that where more than 1.5 inter quartile distances away from the quartiles (this is a standard method to define outliers in a box plot). Finally, since a major part of the responding sites (with the exception of indoor activities) had their main business activity in summer, we will concentrate our analysis on the months June, July and August. The time period used for calibration of the models depends on the specific site. For 67%, the latest available year is 2013, for 28% it is 2012. Further, the number of years used depends on the site and ranges from 1 to 10 years, where the median is 4 years.
Daily weather data is taken from the E-OBS-data set [42-44]. We use this data set for two reasons. First, since it is available for the whole of Styria. Second, the analysis could be repeated throughout Europe and would still be comparable. Unfortunately, the dataset only contains data on temperature, precipitation, and air pressure which does not allow for the computation of more sophisticated weather indices like physical equivalent temperature [18] or aesthetical parameters like cloud cover. Hence we will only use daily maximal temperature and precipitation to represent the weather condition on a single day.
In the second part of the paper we provide a simple warehouse model to estimate the possible value of the previously established WEDDA forecasts. For this demonstration we have chosen one specific site from each category. In principle the sites were chosen arbitrarily but the selection fulfils the following three criteria: First, there is a significant effect of weather on visitors. Second, the daily number of visitors of the site is reasonably high. Third, the facility provides a long time series of observations (the selected sites provide 616 observations for bathing, 638 observations for outdoor and 509 observations for indoor). For these three sites we multiply the visitor numbers with a factor such that the average number of visitors per day amounts to 500. This is done for two reasons. First, to assure that one cannot draw any conclusions from the number of visitors to the recreation site, i.e., that anonymity for the recreation site is provided. Second, to make the results of the modelling comparable between the chosen sites.
In this section we describe the methods used for analysing the data. In subsection 3.1 we describe the methods that are used to establish the WEDDA demand function and in subsection 3.2 we describe the warehouse model in more detail.
WEDDA of leisure activities
To estimate the effects of various weather conditions on the different recreation sites we use general additive models (gam) [45]. General additive models with shape constrains (scam) [46]. In a classical generalized linear model, a transformation of the mean is approximated by a linear combination of the predictor variables. In a gam model this linear combination is replaced by linear combination of smooth functions of the predictor variables.
Altogether we implemented four different models to carry out our Weather Driven Demand Analysis (WEDDA) on the number of visitors. The first model consists of approximating the visitors on a given day by the average number of visitors in the test period. We will refer to this model as model “mean”. The other models are of the gam respectively scam type. For these models we use a logarithmic link function and a quasipoisson distribution family. The second model is our “reference model” which only considers calendric effects i.e.,
Vi ~ Yi + Wi + Mi
Where the number of visitors on a day i (Vi) is related to the year Yi (as numeric variable), the month Mi (as factor) and the day of the week Wi, which also includes the categories bank holiday and bridge day (defined as a single day between a bank holiday and the weekend, also as factor). In order to illustrate the effects of weather on the demand, we added the daily maximum temperature (txi) and daily precipitation in mm (rri). Both enter the equation as a smooth function, where the smooth function s(rri) can be either increasing or decreasing. This leads to the third model:
Vi ~ Yi + Wi + Mi + s(txi) + s(rri)
Which we will refer to as the “WEDDA forecast model”. Our aim is to investigate whether including weather variables into the forecast procedure improves the reliability of the model substantially which in turn comes to the company as direct cost savings.
Finally, we employ another model to investigate the importance of the accuracy of the weather forecast for the prediction. Therefore, we use a coarse temperature index, i.e., temperature rounded to 5 degrees (txi5) (as a factor variable) and a dummy variable that indicates a day with precipitation greater than 0.1 mm (rri0). This leads to the fourth “approximation model”,
Vi ~ Yi + Wi + Mi+ txi5++ rri0
We used and compared all four models to predict future demand for a given recreation site.
Warehouse model
To determine the economic value (i.e., the savings) of a weather based demand model, we use a simple probabilistic warehouse model [37], but we will modify it to fulfil our needs. We assume that the recreation site sells a perishable good where the inventory level has to be determined in the morning and the remaining goods have to be disposed at the end of the day. So the decision between producing too much or too little is the actual optimization problem of the site manager. We denote the cost per remaining unit by pc and the loss per customer that is not served because the site ran out of the product by tl (e.g., marginal return or loss in sales minus marginal costs). At the end of day i, the loss due to insufficient match between supply and demand is given by
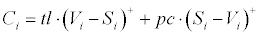
where Si denotes the number of goods held on stock and the (.)+ defines the positive part of a number, i.e., (x)+ = max (x,0). Without loss of generality we will assume that tl = 1 (i.e., we use the costs of not served customers as monetary unit) and use different values of pc, i.e., the relation of the costs of one remaining good to the opportunity of one not sold good. For simplicity we will assume that the manager uses Si = cPi, where Pi is the predicted demand for day i from one of the demand forecast models in subsection 3.1 and c is chosen by the manager in order to minimize the total inventory costs per season, 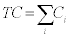 , over an estimation period. In this case the estimation of the models as well as the calculation of C is done for the same period. The value C can be seen as a safety loading to prevent that the site runs out of stock.
, over an estimation period. In this case the estimation of the models as well as the calculation of C is done for the same period. The value C can be seen as a safety loading to prevent that the site runs out of stock.
The evaluation of the model is done over a test period consisting of the season 2012 (The last year where data exists for all chosen sites which consists of 83 observations for bathing, 92 observations for outdoor and 84 observations for indoor). The other years are taken to estimate the models. We assumed perfect accuracy of weather forecasts and hence used the observed weather instead of a forecast for our prediction.
Results for the influence of weather on demand
First, we address the question of predictability of visitors in general. The variable for daily maximum temperature (tx) was significant for 55 out of 63 sites (5 indoor and 3 outdoor activities are not significant), whereas precipitation was only significant for 33 out of 63 sites at a 5%-level. As a measure for goodness of fit, the adjusted R2 was taken. To extract the influence of weather parameters on the reliability of the model, we provide the R2 for the model with weather variables as well as for a model without weather variables.
The values of R2 are depicted in Figure 1 against the mean daily visitors. Crosses denote indoor sites, triangles outdoor sites and circles bathing sites. At first we can observe that the prediction worked satisfactorily for most sites with more than 400 visitors on average: The adjusted - R2 is higher than 60 per cent. We conclude that a higher number of visitors at a given site might improve the quality of the prediction. This result is unsurprising since in case of many visitors, the decision of one individual visitor has less influence on the overall number of visitors.
By comparing the models of three different categories, we can observe that prediction for bathing works well in general since most parts of the reduction in variance is due to weather. For most outdoor activity sites, predictions work well but weather has a significantly smaller effect than for bathing. Finally, for indoor activities the prediction works well for only a few sites. Here we have to mention that we generally observe fewer visitors in indoor facilities than in other sites. Nevertheless we observe that even for some indoor sites, weather can have a significant effect on the variation of visitors.
In a second step we considered the relation between the number of visitors and temperature. In Figures 2-4 we illustrate all estimated smooth functions of the gam model for temperature for those sites where the adjusted R2 is above the value of 0.4. Note that we used a logarithmic link function, which means that when the temperature changes from a value t1 to a value t2 (and all other variables stay constant), the demand changes by a factor exp (f(t1) – f(t2)), where f denotes the function estimated by the gam model depicted in Figure 2.
The black line illustrates the weather dependence for the specific site that is used in the warehouse model. Although the curves for the different sites in each of the three categories may differ substantially, we can identify a typical pattern for each category of sites. We can observe that the specific site that is used in the warehouse model is well inside the typical pattern of the other models and can therefore be seen as representative for this type of activity.
For outdoor activities (Figure 2) the typical pattern consists of an increase up to a given point (for the black line this point is at approximately 27°C), whereas for higher temperatures the number of visitors decreases again. The classical interpretation of this situation is that for outdoor activities good weather is important, which can be usually related to temperature. But at some point, the temperature gets too high to be comfortable for the considered activity and less people visit the site. This type of relationship is well established in the literature. Who investigated the domestic and foreign overnight stays in Austria [7,18-20,26].
We can observe that for bathing, (Figure 3) there is a monotone increasing link between temperature and visitors. It seems that this connection is concave. Presumably there is a threshold temperature when bathing becomes enjoyable for most potential bathing guests and from this point on the increase in additional guests is less steep (For the black line this point is at approximately 29°C). Unlike for outdoor activities, we can observe that higher temperatures do not lead to a decrease in demand. This is in contradiction to the findings [13]. One explanation for this contradiction is that as temperature improves, bathing might not get more enjoyable but other activities might get less enjoyable and hence more people decide to go bathing when temperatures are increasing.
Finally, for indoor activities (Figure 4) we observe that for most sites there is a clear negative dependence between visitors and temperature (For the site with positive dependence, daily maximum temperature is not significant). This does not come as a surprise since indoor activities do not suffer from bad weather as much as outdoor activities and hence are often used as an alternative on days with bad weather.
For the three sites that are used in the warehouse model, we provide more details on the fitted models. As mentioned above we used test and estimation sets for our models. In Table 1 we provide the 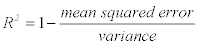 the selected sites for the test period, when the model parameters were estimated with the estimation set. We provide results for the three models reference, WEDDA forecast, and approximation. We do not provide results for the model “mean” since this model has an R2=0 by definition. We observed that with the exception of outdoor sites, the model using only calendric effects (reference) performed rather poor, sometimes even worse than just using the average. Note that in this case, the R2 can be negative since it is calculated for the test period, not for the whole period for which the models were calibrated. The mean squared error for the test period is therefore larger than the overall variance. Nonetheless, a negative goodness of fit value can be interpreted as a poor model performance. We should note that in July of the test year 2012, there was extreme heat followed by bad weather. So 2012 can be seen as a summer with varying weather conditions. Another interesting observation is that already an approximate use of the weather variables (approximation) led to a significant improvement of the reference model and the result is close to the model that uses smooth functions for prediction (WEDDA forecast). At this point we should remind the reader that the weather data that is used for the calculations is still rather crude, so there is room for further improvements.
the selected sites for the test period, when the model parameters were estimated with the estimation set. We provide results for the three models reference, WEDDA forecast, and approximation. We do not provide results for the model “mean” since this model has an R2=0 by definition. We observed that with the exception of outdoor sites, the model using only calendric effects (reference) performed rather poor, sometimes even worse than just using the average. Note that in this case, the R2 can be negative since it is calculated for the test period, not for the whole period for which the models were calibrated. The mean squared error for the test period is therefore larger than the overall variance. Nonetheless, a negative goodness of fit value can be interpreted as a poor model performance. We should note that in July of the test year 2012, there was extreme heat followed by bad weather. So 2012 can be seen as a summer with varying weather conditions. Another interesting observation is that already an approximate use of the weather variables (approximation) led to a significant improvement of the reference model and the result is close to the model that uses smooth functions for prediction (WEDDA forecast). At this point we should remind the reader that the weather data that is used for the calculations is still rather crude, so there is room for further improvements.
| Reference | WEDDA Forecast | Approximation | |
|---|---|---|---|
| Indoor | -0.039 | 0.62 | 0.58 |
| Outdoor | 0.44 | 0.73 | 0.68 |
| Bathing | -0.07 | 0.77 | 0.74 |
Notes: As models we used a model without weather variables (Reference), a model including weather variables (WEDDA Forecast), and a model using only coarse weather variables (approximation).
Table 1: Mean square error (R2) for the test set for the recreation sites used in the warehouse model.
Results for the warehouse model
For the three different kinds of activities we provide the results for the warehouse model for the test season of 2012 (June-August) and the chosen recreation sites in Tables 2-4.
| Model\(pc/tl) | 2 | 1.5 | 1 | 0.5 | 0.1 | 0.01 |
|---|---|---|---|---|---|---|
| Mean | 33100 | 30800 | 27700 | 21700 | 9540 | 1790 |
| Reference | 27400 | 24000 | 19700 | 13400 | 4580 | 882 |
| WEDDA Forecast | 18000 | 16200 | 13800 | 9910 | 3340 | 637 |
| Approximation | 20200 | 18100 | 15100 | 10700 | 3960 | 688 |
| Savings (Reference vs WEDDA Forecast) | 9400 | 7800 | 5900 | 3490 | 1240 | 245 |
Notes: The stock for each day is estimated with the average number of visitors (mean); the model that only considers calendric effects (reference); the model that contains smooth functions of weather variables (WEDDA forecast); the model that uses approximate weather variables (approximation). Finally, the difference between reference and WEDDA forecast is provided as savings.
Table 2: Total inventory cost per season (TC) for one chosen outdoor recreation site.
| Model\(pc/tl) | 2 | 1.5 | 1 | 0.5 | 0.1 | 0.01 |
|---|---|---|---|---|---|---|
| Mean | 32000 | 30100 | 26900 | 19200 | 6760 | 1210 |
| Reference | 32600 | 30700 | 27600 | 20500 | 7050 | 1200 |
| WEDDA Forecast | 12600 | 11300 | 9690 | 7100 | 2570 | 360 |
| Approximation | 15900 | 14300 | 12300 | 8730 | 2530 | 313 |
| Savings (Referencevs WEDDA Forecast) | 20000 | 19400 | 17910 | 13400 | 4480 | 840 |
Notes: The stock for each day is estimated with the average number of visitors (mean); the model that only considers calendric effects (reference); the model that contains smooth functions of weather variables (WEDDA forecast); the model that uses approximate weather variables (approximation). Further the difference between reference and WEDDA forecast is provided (savings).
Table 3: Total inventory costs per season (TC) for one chosen bathing recreation site.
| Model\(pc/tl) | 2 | 1.5 | 1 | 0.5 | 0.1 | 0.01 |
|---|---|---|---|---|---|---|
| Mean | 18700 | 17200 | 15200 | 11500 | 4500 | 708 |
| Reference | 18200 | 17200 | 15400 | 12100 | 5080 | 976 |
| WEDDA Forecast | 12200 | 10900 | 8890 | 6050 | 2020 | 330 |
| Approximation | 11800 | 10700 | 9000 | 6280 | 2250 | 351 |
| Savings(Reference vs EDDA Forecast) | 6000 | 6300 | 6510 | 6050 | 3060 | 626 |
Notes: Monetary unit is the costs of not served customers (tl) as monetary unit. The stock for each day is estimated with the average number of visitors (mean); the model that only considers calendric effects (reference); the model that contains smooth functions of weather variables (WEDDA forecast); the model that uses approximate weather variables (approximation). Further the difference between reference and WEDDA forecast is provided (savings).
Table 4: Total inventory costs per season (TC) for one chosen indoor recreation site.
We provide the values of TC, which is the sum of the costs of remaining goods pc plus the costs per customer that is not served tl for a period of 92 days with on average 500 customers per day. Recall that tl = 1, i.e., we use the costs of not served customers as monetary unit. The tables illustrate the costs depending on how the stock Si is estimated: The first model (mean) only uses the average number of visitors. The second model (reference) only considers calendric effects, while the third model (WEDDA forecast) contains smooth functions of weather variables and the fourth model (approximation) uses only approximate weather variables to simulate inaccurate weather forecasts. In addition we provide the savings which is the difference between the expected costs when using the model without weather variables (reference) and the model with weather variables (WEDDA forecast). This can be interpreted as the savings due to the use of weather forecasts compared to a scenario where the manager only uses calendric effects. We implicitly assume that the manager forecasts demand with neither any knowledge of future weather conditions nor the influence of these weather conditions on demand.
We show values of TC for different ratios of pc/tl. A ratio of pc/ tl =2 for example means that the costs of remaining goods is twice the costs for non-served customers, while a ratio of pc/tl = 0.01 means that the costs of remaining goods is only 1% of the costs of a non-served customer. A realistic ratio is hard to choose, given that wasting food has become a disputed issue in western societies and therefor wasting a lot might imply reputation risks also. However, a simple approach might be to consider the marginal cost of production as the cost of disposal (pc) (ignoring possible costs of waste disposals). tl can be interpreted as the difference between the price of the good and the marginal cost, i.e., the marginal return. Therefore it could be argued – since marginal cost can be higher than the marginal return – that ratios higher than one are plausible. On the other hand, the true cost of rejecting customers may be much higher than just the marginal return, for example also because of a loss in reputation. Under this view, ratios smaller than one seem realistic. But which ratio for pc/tl is the closest to reality will heavily depend on the good under consideration, the internal cost structure and the pricing policy of the recreation site.
We focus our discussion of the results for one outdoor recreation site. From Table 2 we see that if the cost for provision of the perishable good is the same as the loss for unsatisfied demand (pc/tl=1), the potential savings by the use of the weather forecasts already amounts to about 5900 times the costs of non-served customers (tc). In general, we can observe that with increasing cost of remaining units pc relative to the loss resulting from unsatisfied demand, the total cost as well as the savings increase significantly by the use of better forecasts. In all cases, the use of weather variables to predict future visitors lead to a significant reduction in t cost, especially for sites where the cost of disposal is high. We can observe that for small values of pc/tl, the difference between the cost of the different models is rather moderate but if marginal cost per unserved customer increases in relation to the marginal return, also small differences in the quality of estimation can have significant effects on the cost structure.
The chosen outdoor recreation site is the only one where prediction using calendric variables leads to an R2>1 (Table 1). We can observe in Table 2 that the R2 = 0.44 is relatively small, but even this model already leads to a significant cost reduction.
The highest savings arise for a chosen bathing recreation site (Table 3). There are two reasons that the savings for the bathing site (17,910 for a pc/tl ratio of one) are much bigger than for the outdoor site. First, the WEDDA forecast works significantly better for the chosen bathing site than for the chosen outdoor site, leading to smaller costs for the bathing site. Second, the reference model for the outdoor site already implies some cost savings over the model “mean”, so parts of the overall reduction in costs can already be attributed to the calendric effects.
The savings for the chosen indoor recreation site (Table 4) are in general comparable to those from outdoor activities. Further it is apparent that the reference model and the “mean model” work comparable, this means that for the considered recreation sites, the number of visitors are not heavily influenced by calendric variables (e.g., day of the week). The difference between the approximation model and WEDDA forecast is again comparable to that of the chosen outdoor facility. In addition, we can observe that the chosen indoor recreation site achieves the lowest costs compared to bathing and outdoor by the use of WEDDA forecasts. At the first glance, this is surprising since the WEDDA forecast for the indoor recreation site has the smallest R2 (Table 1). On the other hand, we can observe that also the model “mean” for indoor recreation sites implies the smallest costs of all three chosen sites. This means that although the absolute costs when using WEDDA forecast are the lowest, also the cost reduction that can be achieved compared to the model “mean” are the lowest.
In this paper we have studied the link between the demand and weather variables for a variety of recreation sites. While for bathing sites there is an increasing relationship between temperature and demand, the demand is typically increasing up to a given threshold temperature and decreases afterwards for other outdoor sites. Unsurprisingly, indoor activities display a negative dependence between temperature and demand. While the prediction of demand with weather variables works well for most outdoor activities including bathing (adjusted R2 > 0.6), this is not the case for most indoor activities. Nevertheless there exist indoor sites where demand can be predicted reasonably well by a WEDDA-forecast.
Of course, the weather dependence of various recreation activities implies substitution effects to occur between different activities. In order to quantify these effects, one could consider a multivariate model. Note that these substitution effects may not only occur between different activities but also between different facilities of the same type since single facilities may be affected adversely by the weather. However, this point can be subject to future research.
Furthermore, we have analysed the economic effects of the use of weather forecasts for three different sites. We showed that for the chosen sites, the inclusion of weather forecasts in demand management can lead to a significant cost reduction, even if we only use a rough approximation measure for the daily maximum temperature.
For reasons of simplicity, we have considered inventory costs as a reasonable proxy for all costs that arise from false demand estimation. In practice, costs (and therefore savings) would probably consist of expenditures for (unemployed) staff to a substantial part. The implicit assumption we made is that the manager of a recreational site is able to react to fluctuating demand at all. This issue adds to further possible complications associated with the implementation in practice, since the legal issue, whether weather risks can be transferred from the company to the employees is certainly treated differently in different countries.
The savings depending on the pc/tl ratio pointed out that cost reductions can be especially useful for sites where the costs of disposal are high. In other words, weather driven demand analysis (WEDDA) makes a lot of sense for sites where wrong production decisions are costly.
This research received financial support from the Provincial Government of Styria, under the GTR-project “Wissen”.