The breaking up of double helix into single helix DNA is called the DNA denaturation or thermal DNA melting. Theoretically, the phenomenon has been discussed in many works, for instance the work by Hanke et al. on the denaturation of stretched DNA [1]. The opening double-stranded DNA can be explained by a force exceeding a certain critical value [2-4]. It is possible that the local opening of DNA bubbles in the selective regions without breaking the whole DNA [5]. In other cases, the denaturation can also be influenced by many factor such as the alkaline compound filling up a cell, liquid surrounding DNA and other external potential [4-8]. It has been shown that a bell shaped soliton exists in the DNA chain when the effect of viscosity is taken into account [9,10]. The melting temperature as well as the critical force that is required to unzip the DNA molecule depend on the salt concentration of the solution [11,12].

One of the physical model that have been discussed by researchers is called the Peyrard-Bishop (PB) model [13,14]. This model basically considers the DNA as two mutually hand in chains with the Morse as the interaction potential. The model can explain the denaturation process along with its thermodynamical properties. The external factor is usually calculated by considering an additional term to the morse potential. For example, the external potential in the form of Gaussian will strengthen DNA separation process at low temperature [6]. In the Monte Carlo experiment the unzipping processes due to the external force probed show the dependence of the unzipping forces on unzipping speed and temperature [7]. Other papers show that the viscosity which is represented by an external potential affect the process of denaturation i.e., strengthen or weaken, depending on the type of fluid [12-17].

In the dynamical consideration i.e., solution of the equation of motion, show that the separation of double helix propagate as a soliton and the dynamical properties depend on the interplay between dispersion and nonlinearity [10,11]. Furthermore, the interaction between the external and viscous force has interesting consequences. One of the consequences is the propagation of localized separation of DNA (DNA bubble) in term of the breathing soliton [8]. The interaction between the solvent and helicity of DNA show the breather drastically depends on the twist angle and solvent interaction [9]. It is very important to know how the interaction of these two forces have an effect on the thermodynamical properties of DNA denaturation. This issue becomes the primary focus in this paper.

It is well known that the calculation of the external effects to the denaturation processes of DNA is done with the transfer integral [13,15,16] and path integral methods [18,19]. Mathematically, the transfer integral methods is a transformation of the integration problem into eigen value problem where in this case becomes the time independent Schrodinger equation. The calculation on model block DNAs shows that the method is considerably more efficient than molecular dynamics simulation [15]. It can calculate the partition function to get the average displacement from equilibrium as a function of temperature. This method is also successful to predict the bubble formation and the effect of force on DNA unzipping [16]. Another hands, for the special case, if the external potential is treated as a small perturbation then the first order perturbation theory can be applied. This yields a smooth denaturation transition for homogeneous DNA [6]. If the external factor is considered, the path integral approach becomes the general case because the perturbative approximation is not used. The partition is found by calculating all possible path (a sum over all histories) function between the initial and final conditions under consideration. The application of the path integral method for DNA denaturation was done by ref. [18,20] where the thermal behaviour was studied by calculation the particle paths running along the imaginary time axis in the PB Euclidean action.

In this paper we use path integral Monte-Carlo (PIMC) with Metropolis algorithms as a main algorithm in this numerical scheme. The viscosity and external forces will be expressed as additional potential term in the PB Hamiltonian. Calculation of the partition function to find the mean stretching distance of the hydrogen bond is done by using the PIMC. This paper is organized as follows. First, the PB model with viscous and external potentials is briefly introduced. It is then followed by the statistical mechanics formulation of the partition function of Hamiltonian under consideration. Before closing the paper with summary, the detailed calculation of hydrogen bond stretching using PIMC methods and its thermal behavior are presented.

It is well known that the most successful DNA model to study the Denaturation processes is the PB model. The motion of DNA molecules is represented by transversal displacement, u_n and v_n , corresponding to the base displacement from their equilibrium position along the direction of hydrogen bonds that is represented by the Morse potential to connect two bases in a pair [13]. The PB model with an additional external potential V which has the same direction as Morse potential [13],

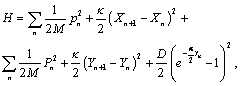(1)

where D and α are the depth and inverse width of the potential respectively. 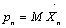, 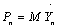and κ is the spring constant. 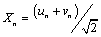and 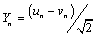are in-phase and out-phase transversal motions respectively. In the PB model, the variable X_n is decoupled from Y_n corresponding merely to the linear chain, while Y_n represents the stretching motion which is our main interest. The viscosity of the liquid surrounding DNA will give dissipative effect in the DNA system. The effect should appear explicitly in the PB model. In general, it is written in the new form as,

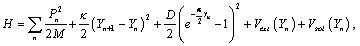(2)

Where V_ext (Y_n) an external potential and the solvent potential is given by ref. [17,20],

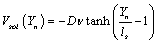(3)

Where ν is the viscosity coefficient (a dimensionless factor), ls and D are the length scale of DNA and Morse factor respectively. The various external potentials that will be used in this studies are constant potential V_ext (Y_n) = V₀ and the Gaussian potential 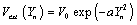with a being a constant. The Gaussian potential will be an instantaneous linear potential if we take limit of the standard deviation goes to zero.

The denaturation process is a thermodynamics phenomenon thus it can be studied in the statistical mechanics framework. In this theory, we consider the partition of energy in the system that is represented by the partition function [6]. This,

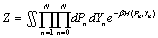(4)

Where β =1/(k_BT) is a Boltzmann factor with k_B is a Boltzmann constant and T is a temperature. The relevant parameter in the study of DNA denaturation is the mean stretching ⟨Y⟩, of the hydrogen bond. It is defined as,

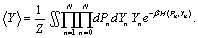(5)

The calculation of this quantity is the focus of this paper and will be solved by path integral Monte-Carlo methods.

Thermal Properties by Path Integral Monte-Carlo Approach

This section is intended to solve (5) by path integral monte carlo (PIMC). The employing of PIMC as a proposed method is based on the consideration that the Hamiltonian H in the above equation has high complexity of variables. This problem is more complex than [6,8] and it is impossible to use analytical methods.

Let we write the partition function (4) as,

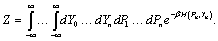(6)

Then discretization of the partition function is calculated by 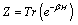(7),

(7)

where H is Hamiltonian that was defined in the problem as we concerned.

The last equation can be calculated numerically and based on the following steps [21,22]. At the first step, an initial path is generated by choosing N random number. This path is notated as x=(x₁,x₂,…,x_N) between the initial and final position. Then a suggested modification of the path is made by displacing the i-th node in the path where i is random integer between 1 and N (i-th node is i-th base pairs in DNA double strands). By this technique, the action of 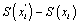is calculated where x_i^' is a random point between [x_i - Δ_x , x_i + Δ_x] The total 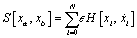In this case x_a and x_b are periodic boundary condition of DNA strands, meanwhile ∈ is a parameter with small value that has been chosen. In our simulation we set N= 10,000 and each time the iteration reach x value of boundary condition we give zero for the action function. Hence the mean of Y is approximated by

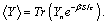(8)

In the calculation, we use the set of parameters D = 0.04 eV, 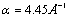, , 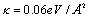v = [0.0001, ,0.025] and l_s=5Å and [6,17]. The initial condition are taken to be the same as Zoli [17]. The first simuation considers the denaturation processes with constant and gaussian potentials. It is depicted in Figure 1. The result shows that the external force will decrease the melting temperature where the same result was also obtained by Sulaiman et al. [6] by using the transfer integral method. The decreasing of the melting temperature due to external forces such as random force and instantaneous force has been confirmed by other researchers [2-4]. At this time the transfer integral method gives the similar result comparing with the path integral methods.

Figure 1: The path integral simulation of the hydrogen bond stretching as a function of melting temperature for constant potentials (dashed line) and Gaussian potential (solid line).

The interesting case when we consider the effect of viscosity is represented by applying tanh(Y_n) potential. The analytic solution cannot be obtained by the transfer integral method due to divergence of the average displacement integration. The numerical calculation by using path integral method is depicted in Figure 2. The result shows that the viscous potential will open the double helix locally by certain distance from its original position. For the case of the external viscosity potential is low, the DNA will be opened at 300K and toward to the saturation point above 500K. The saturation point is inverse proportional to the coefficient of viscosity. The increase of the viscosity will decrease the saturation point. The result of the experiment shows that the increase in melting temperature against the liquid depends on the strength of an ionic liquid [23]. Generally melting temperatures will rise if concentration of the positive charge is rising but decrease if solvent is more negatively charged. This paper does not take into account the charge as a factor as it is a challenging work, and can be done in future studies.

Figure 2: The hydrogen bond stretching as a function of melting temperature for viscous potentials with V_ext=0 and variation of ν, ν=0.001 (solid line), ν=0,015 (dashed line) and ν=0,025 (dashed-dotted line).

The interplay between the external force with the viscosity gives an interesting result depicted in Figure 3. The result shows that when the Gaussian external force apply to the DNA then the viscosity coefficient 0.1 will prevent the separation of double helix into the single helix. The average displacement is only about 10 Å and tends to be constant at 380K. The increase of the viscosity coefficient will decrease the saturation point. For example if the viscosity coefficient is about 0.1 then the saturation point achieved around 400K with the hydrogen stretching is about 11 Å. This effect is also found in the dynamical system approach i.e., the consideration of solving the equation of motion. Equilibrium between the external force and the viscosity will give more effective propagation of the DNA bubble [8]. The other results show that the width of the pulse of soliton increase when we increase the solvent viscosity coefficient [9].

Figure 3: The hydrogen bond stretching as a function of melting temperature for fixed Gaussian potential and variation of coefficients viscosity ν=0 (solid line), ν=0.001 (dashed-dotted line), ν=0,01 (dotted line), ν=0.1 (dashed line)

Further, the variation of the viscosity coefficient and the amplitude of the Gaussian force with variation of the denaturation temperature is depicted in Figure 4. Each curve corresponds to different denaturation temperature. For example the diamond-dotted line is a curve at the denaturation temperature is 400K. The region where the viscosity coefficient is higher than 0.02 can be labeled the saturation region. It means that the DNA is not perfectly open (opening without fully denaturing) but separates only a certain displacement. This is called the saturation displacement. When the amplitude of the external potential is higher than 0.35 V then the DNA perfectly open, so this region is called a denaturation region. The last region to consider ia the area similar to the denaturation without external and viscous forces. The external effect has a significant influence if the amplitude of the external potential higher than 0.35 V and the viscosity coefficient is higher than 0.02. The figure shows that for high temperature the external force more important than the viscous force but the opposite is true at the low denaturation temperature. In low temperature then the effect of viscosity more a role. For the denaturation temperature below 300K then the dna will not experience saturation, in other words it will be unzipped perfectly.

Figure 4: Variation of the viscosity coefficient and the amplitude of the Gaussian force with variation of the denaturation temperature.

As a preliminary investigation we briefly concern temperature at 300K, our simulation gave results of Figures 5-7. Figure 5 is graphical surface (three dimensions curves) to describe denaturation of DNA. At Temperature 300K backbones of DNA are separated at 2 Å in absence of viscosity parameters and no external force. If we increase the value of viscous parameter then DNA will be compressed (Figure 6), hence if we give external potential, the distance will rise exponentially (Figure 7).

Figure 5: Three dimensions graph of stretching hydrogen bond distance depends on viscosity parameters and potential external at T=300K.

Figure 6: Stretching hydrogen bond distance respect to viscosity parameters with variations of potential externals at T=300K.

Figure 7: Stretching hydrogen bond distance respect to potential externals with variations of viscosity parameters at T=300K.

The behavior of the temperature-curves in combinations of viscosity parameters respect to external potential is given in Figure 4. We are able to define obviously three regions, firstly the region where DNA experiences displacement from the origin, secondly DNA sustains denaturation with length saturation close to original distance, finally the region where DNA gets total structural change from double strands to single strands. Based on the Figure 4 the temperature near 337.5K is of great concern, since the DNA has two state. Each backbone of DNA separates linearly then move away as long as it can. When viscosity coefficient is lower than ν=0.02, and external potential is lower that 0.25 the DNA is close to normal hydrogen stretching distance; meanwhile the increasing external potential parameters influence, DNA to start melting process. The separation of double strands in DNA will be saturated to 10 Å when we take viscosity parameters higher than 0.02. The situation drastically differs for temperature higher than 337.5K, domination of external force give significant effect to make double strand of DNA separated.

In this paper we also report the situation when DNA temperature reaches 337.5K, the simulation gave results in Figures 8 and 9. These figures describe the double stranded DNA strands are almost separated, we find that external potential 0.35 volt can compensate variations of viscosity parameters.

Figure 8: Three dimensions graph of stretching hydrogend bond distance depends on viscosity parameters and potential external at T=337.5K.

Figure 9: Stretching hydrogen bond distance respect to viscosity parameters with variations of potential externals at T=337.5K.

The calculation of the partition function was done by using path integral Monte-Carlo (PIMC) and then the stretching of hydrogen bonds is finally obtained. Based on these numerical results, the viscous effect and the external forces on thermal DNA denaturation of Peyrard- Bishop model was investigated. The viscosity potential was represented by tanh(Y_n) function and the external forces ware represented by the constant and Gaussian potential. When the Gaussian external potential is applied to the DNA then the viscosity will prevent the separation of double helix into the single helix. The increase of the viscosity coefficient will decrease the melting temperature. It can be concluded that for high temperature the external force is more important than the viscous force but the opposite happens that at the low denaturation temperature.

Our work also reported that there are some regions can be defined based on temperature dependency of viscosity parameters and external potential. The region where external potential is less than 0.35 V, the double helix DNA will open with saturation stretching distance, other case if we increase external potential in our simulation there are not effect for DNA in under 337.5K temperature regime. The distinction will appear when the temparature bath is higher than 337.5K. At the temparature 337.5K we found that DNA would change drastically from double strand structure to become single strand structure. When we set in an external potential of 0.35 V and studied variation of viscosity parameters in our simulation, we found that DNA would almost experience denaturation process.

The authors would like to thanks to ministry of research technology and higher education, Republic of Indonesia for supporting this work by providing grant Desentralisasi 2015, Research KK ITB 2015, and Riset Peningkatan Kapasitas 2014-2015. AS thanks Riset- Pro Kemenristek for financial supported. One of the authors, WH would like to thank to ministry of research technology and higher education, Republic of Indonesia for PhD Scholarship program.