Journal of Research and Development
Open Access
ISSN: 2311-3278
ISSN: 2311-3278
Research Article - (2024)Volume 12, Issue 3
A Late Heavy Bombarment (LHB) era occurred from 4 Gya to 3.8 Gya characterized by a cataclysmic spike in cratering events on our Moon as analyzed by Moon’s Apollo mission. It is hypothesized that this spike occurred due to Mean Motion Resonance (MMR) 1:2 of Jupiter and Saturn. The Solar System was precipitated from the Solar Nebula at 4.567 Gya. In 7 My Jupiter was born that is at 4.56 Gya. In 30 My gas giants and ice giants were formed at 4.537 Gya and in 100 My terrestrial planets (Earth, Mars, Venus and Mercury) formations were completed. Based on the new perspective of the birth of planets and exo-planets it is postulated that Jupiter and Saturn born at first Clarke’s orbits fall into super-synchronous orbits and are launched on expanding spiral orbit. If Saturn is born 25 My later than Jupiter, MMR 1:2 crossing occurs 300 My later than the birth of Jupiter. This MMR crossing acts as a stimulus and Neptune is launched on an outward spiral path towards Oort’s Cloud resulting in a heavy shower of comets and asteroids from Oort’s Cloud to the inner part of solar system resulting in a catacalysmic spike in cratering rate during Late Heavy Bombardment Era (LHB Era) from 4 Gya to 3.8 Gya. Clearly there is 500 My delay from the birth of Jupiter to the LHB era whereas MMR 1:2 crossing of Jupiter Saturn occurs 300 My from the birth of Jupiter. This extra 200 My delay occurs due to delayed response of Neptune. This point needs to be examined through further research.
Hilda asteroids; Mean motion resonance 1:2; Late Heavy Bombardment Era (LHB Era); Oort’s cloud; Mean motion resonance dip curve
In a time window corresponding to Neohaedean and Eoarchean era on Earth a Solar wide hypothetical event occurred between 4.1 billion years Ga to 3.8 Ga ago which resulted in a spike in cratering events followed by declining cratering events. This was considered by the scientific community as Late Heavy Bombardment (LHB) era or Lunar Cataclysm. Is it a putative, brief spike in cratering rate at ~3.9 Ga ago preceded by a low cratering rates? Are these enhanced impacts due to planetesimals left-over from terrestrial planet formation? A nice terminal cataclysm model exists to explain LHB era [1]. This nice model explains the terminal cataclysm as well as many other long standing problems in solar system dynamics. According to this Model Jovian planets were the earliest to form on initially nearly circular, coplanar orbits with a more compact configuration (all were between 5 AU to 15 AU) than they have today. The author has his own dynamical Kinematic Model to explain the migration of Jupiter, Saturn, Neptune and Uranus and in this paper author’s model will be followed [2]. Before the introductory chapter is closed it will be appropriate to mention that an alternative theoretical explanation exists for LHB era namely:
LHB era could be the tail end of monotonically decreasing population originally produced by planet formation process in the inner solar system [3]. This is known as Declining Bombardment Hypothesis (DBH). In this paper we will move along the dynamical model set by the author [2].
The new perspective of solar system formation and evolution
In recent days four observations strongly suggest that in remote past Jupiter and the gas giants may have experienced gravitational sling shot and they may have been launched on an outward spiral path just the way Moon has been launched (personal communication: http://arXiv.org/abs/0805.0100) or for that matter all planetary natural satellites have been launched [4].
The first observation-700 Hilda asteroids in elliptical orbit [5]. The asteroid belt is populated with hundred thousands of rocky remnants leftover from planet formation. These are called asteroids and they lie between Mars and Jupiter orbit between a radii of 3 AU to 10 AU. Most of the asteroids are in near circular orbits. There are 700 odd asteroids known as Hilda asteroids which are in highly elliptical orbit and these eccentricities could have been imparted only by a migrating Jupiter set on an expanding spiral path. The migrating Jupiter first ejected some proto-Hilda asteroids out of the system and next elongated the orbits of the residual asteroids. The migrating Jupiter could have also set the planetary embryos on unruly chaotic paths which led to infrequent collisions and accretion resulting into terrestrial rocky planets.
Through computer simulation studies it has been shown that our planetary system, with initial quasi-circular, coplanar orbits, would have evolved to the current orbital configurations provided Jupiter and Saturn crossed the mutual 1:2 Mean Motion Resonance (MMR) [1]. When the ratio of the orbital periods of Jupiter and Saturn is 1:2 it is the strongest resonance point. At all integer ratios resonance is obtained but the maximum is obtained at 1:2. The resonance crossings excite the orbital eccentricities and mutual orbital inclinations to the present values. Jupiter, Saturn and Uranus have the present eccentricities of 6%, 9% and 8% respectively. The present mutual inclination of the orbital planes of Saturn, Uranus and Neptune take the maximum values of approximately 2° angle with respect to that of Jupiter. The simulation was started with the initial positions of Jupiter and Saturn at 5.45 AU and 8 AU respectively. 1:2 MMR crossing occurs at 8.65 AU Jupiter orbit. The present orbital semi major axes of Jupiter, Saturn, Uranus and Neptune are 10 AU, 15 AU, 19.3 AU and 30 AU respectively. This simulation reproduces all aspects of the orbits of the giant planets: Existence of natural satellites, distribution of Jupiter’s Trojans and the presence of main belt asteroids.
The presence of Jupiter’s Trojans can be explained only by 1:2 MMR crossing by Jupiter and Saturn [6]. Trojans are asteroids which are in the same orbit as that of Jupiter but they are leading or lagging by 60° angle in their co-orbital motion.
The petrology record on our Moon suggests that a cataclysmic spike in the cratering rate occurred approximately 700 million years after the planets formed [7]. With the present evidence we assume the birth of our Solar Nebula at 4.56 Gya. The formation of gas giants and ice giants was completed in first 5 million years and Earth was completed in first 30 million years. This puts the date of completion of giant planets at 4.555 Gy and the date of completion of the terrestrial planets particularly Earth at 30 million years after the Solar Nebula was born that is at 4.53 Gya. At 4.53 Gya, the giant impact occurred and from the impact generated circum-terrestrial debris, Moon was born beyond Roche’s limit at 16,000 Km orbital radius. By gravitational sling shot effect it was launched on an expanding spiral path [4]. Presently Moon is at the semi-major axis of 384,400 Km with a recession velocity of 3.7 cm/year as measured by lunar laser ranging experiments [8]. Towards the end of planet formation phase, the residual debris of the Solar Nebula was being rapidly sucked in or swept out of the system. This resulted in heavy meteoritic bombardment of all the big sub-stellar objects including our Moon. Through Apollo mission studies it has been determined that there is a sharp increase in the bombardment rate and hence in the cratering rate around the period of 4.5 Gya to 3.855 Gya on our Moon. From this it is concluded that there was a cataclysmic Late Heavy Bombardment of all big sub-stellar bodies, including our Moon, at about 700 My after the completion of formation of Jupiter and Saturn.
As a result of this outward migration considerable eccentricities were imparted to 700 odd Hilda asteroids [5]. Furthermore through simulation study it is concluded that during the course of orbital evolution when 1:2 MMR crossing occurs the stimulus for Late Heavy Bombardment Era (LHB Era) is triggered [7]. We know that LHB Era lasted from 4 Gya to 3.8 Gya. Hence any satisfactory and adequate theory of migration of giant planets must explain this particular date of triggering of LHB Era. Meaning by if indeed the new perspective on the birth and evolution of solar system is a realistic picture of two body problem then we should be able to show the 1:2 MMR crossing in this time window of time line of birth and evolution of our solar system [9,10].
The methodology of analyzing the causative factor of LHB Era is the methodology adopted in reference Sharma et al. [4]. The assumed timeline of birth and evolution of our Solar System is given in Table 1.
| Triggering | Birth of solar nebula |
Dissipation of gas and dust disk |
Last giant impact | Late heavy bombardment | Life |
|---|---|---|---|---|---|
| 4.568 Gya | 4.567 Gya | 4.558 Gya | 4.468 Gya | 4.0 Gya | 3.568 Gya |
| 0 | 9 My | 99 My | 567 My | 999 My | |
| Triggering | A supernova explosion in our neighborhood generates shockwaves which sets a passing-by interstellar cloud of gas and dust into spin mode. This spinning primordial cloud flattens into a pancake like disc of cloud and dust. | ||||
| Birth of solar nebula | The dust particles may be colliding and sticking giving rise to pebble sized solids. These pebbles further coalesce to form km-size planetesimals. This formally marks the birth of solar nebula and the start of planetary formation. Planetesimals collide and accrete to form planetary embryos. | ||||
| Dissipation of gas and dust disk. | Particles less than micron size and gases are pushed out by photon pressures. This is known as photo-evaporation. Particles of micron size and more are acted upon by Robertson-Poynting drag which constrains these particles to spiral inward and eventually fall into the host body. This leads to gradual dispersal and dissipation of gas-dust disk. By this process all the gas and dust will be removed in 30 My. This means that within this narrow time slot the gas giants should have completed their formation. Hence in first 30 My Jupiter and Saturn should complete their formation. Planetary embryos get enveloped by hydrogen gas through gravitational accretional runaway mechanism terminated by the paucity of material because of a gaping void. When the void gets filled up then the next sequential gravitational accretional runaway process initiated. This process is repeated until all the gases are exhausted. In this way in 30 My Jupiter, Saturn, Neptune and Uranus formation is completed. | ||||
| Last giant impact | The terrestrial planets are not formed by runaway gravitational accretional mechanisms because such large amounts of material is not present to sustain such a process. Instead a series of infrequent and titanic impacts caused the formation of the present sized Earth, Venus, Mars and Mercury. The giant impact was the last such event, atleast in the context of Earth, which formally marked the completion of formation of Earth. | ||||
| Late heavy bombardment era | 1:2 MMR crossing occurred by the spirally expanding orbits of Jupiter and Saturn. This triggered Neptune to be flung into Oort’s Cloud. The disturbance of Oort’s caused a large amount of comets and asteroids to be flung into the inner part of the Solar System. This caused all the planets to experience late heavy bombardment era about 567 My after the birth of Solar Nebula. The foot prints of this era is well preserved in the petrological record of out Moon. | ||||
| Life | 1 Gya the first organic life based on anaerobic fermentation was initiated. | ||||
Table 1: The timeline of planetary formation [11].
It is assumed that Solar Nebula is born 4.567 Gy before the present. While the central part is collapsing into Sun simultaneously Jupiter is born. It is assumed that Jupiter is fully formed in 7 My leaving a gaping hole. That is the age of Jupiter is 4.56 Gy. This paucity of raw material is what terminates the gravitational runaway accretion of Jupiter. Jupiter, due to gravitational sling shot effect, is launched on an expanding spiral path. As Jupiter rapidly spirals out, hydrodynamic stability is restored and the gaping hole in the disc of accretion is filled up with raw material for newer planet Saturn formation. Saturn could have formed 10 My after the birth of Solar Nebula or 15 My after the birth of Solar Nebula or 20 My after the birth of Solar Nebula. The orbital path of both Jupiter and Saturn are plotted for first 1000 My and the evolving semi major axis aS and aJ for Saturn and Jupiter respectively are tabulated and from (aS/aJ)3/2 the Mean motion resonance (2/1) is examined. The cubic power of the square root of (aS/aJ) is the ratio of PS (orbital Period of Saturn) and PJ (orbital Period of Jupiter). 2:1 MMR crossing is examined for simultaneous birth of Jupiter and Saturn, for time difference of 5 My, 10 My, 15 My, 20 My, 25 My with Jupiter birth preceding Saturn.
Saturn cannot be formed any later because in about 30 My the protoplanetary gas-dust disk is completely dissipated by Poynting Robertson Photon Drag and by photoevaporation. In 30 My from the time of Solar Nebula birth all the four Jovian Planets formation should be completed. That is Jupiter, Saturn, Neptune and Uranus birth and formation should be completed sequentially in the descending order of their mass. As the time difference between the birth of Jupiter and Saturn widens, Jupiter birth-date is not pushed back but Saturn’s birth date is pushed back but not beyond 25 My after the birth of Solar Nebula. Keeping this time constraint in mind the possible set of the birth dates are tabulated in Table 2. This set of birth dates are taken while examining the various scenarios of birth and evolution of Jupiter and Saturn.
| Jupiter birth date (Gya) |
Saturn birth date (Gya) |
Difference in the birth dates (My) |
|---|---|---|
| 4.56 | 4.56 | 0 |
| 4.56 | 4.555 | 5 |
| 4.56 | 4.55 | 10 |
| 4.56 | 4.545 | 15 |
| 4.56 | 4.54 | 20 |
| 4.555 | 4.535 | 25 |
Table 2: Set of physically tenable birth dates of Jupiter and Saturn.
The trajectories of Jupiter and Saturn are worked out for this set of birth dates and 2:1 MMR crossing-point examined. The crossingpoints are tabulated in Table 2.
Jupiter’s orbital evolution
The globe parameter of Sun is given in Table 3. The globe and orbit parameters of Jupiter and Saturn are given in Tables 4-6.
| M(kg) | R(m) | C(kg-m2) | Spin period | Jspin(kg-m2-sec-1) | |
|---|---|---|---|---|---|
| Sun | 1.99 × 1030 | 6.96 × 108 | 3.856 × 1047 | 24.9 d | 1.126155405 × 1042 |
Table 3: Globe parameters of our Sun [12-14].
| a(× 109 m) | Alpha -α (inclination angle in degress) | Φ(obliquity angle in degrees) | P1(d) | P3(d) | m(kg) | ρ +(Kg/ m3) | |
|---|---|---|---|---|---|---|---|
| Jupiter | 778.3 | 1.31 | 3.1 | 4,331.865 | 0.41 | 1.90 × 1027 | 1330 |
| Saturn | 1,427 | 2.49 | 26.7 | 10,760.265 | 0.43 | 5.69 × 1026 | 710 |
Note: P1: Orbital period of the Planet; P3: Spin period of the Planet.
Table 4: The globe and orbit parameters of Jupiter and Saturn [12-14].
| B(× 1010 m3/2/s) | R+(× 106 m) | Jspin│+(Kg-m2/sec) | Jorb (Kg-m2/sec) | JT(× 1042 Kg-m2/sec) | E(× 10-16m-3/2) | F(m-2) | |
|---|---|---|---|---|---|---|---|
| Jupiter | 1.152647951 | 71.492 | 6.89^38 | 1.93^43 | 20.42684441 | 45.95926 | 4.9227^-21 |
| Saturn | 1.152262984 | 60.268 | 1.398^38 | 7.83^42 | 8.956295205 | 20.15789 | 1.475^-21 |
Table 5: Tabulation of ω /Ω equation parameters for Jupiter and Saturn (R+=Radius of the Planet and Jspin|+=Spin angular momentum of the Planet JT = ((Jspin)Θ + Jorb + Jspin|+).
| a(× 109 m) | aR(× 109 m) | aG1(× 109m) | aG2(×1011 m) | m(kg) | € | ω /Ω│calculated | ω /Ω│observed | |
|---|---|---|---|---|---|---|---|---|
| Jupiter | 778.3 | 1.7346 | 3.78579 | 8.71161 | 1.90 × 1027 | 0.893 | 173.726 | 173.96 |
| Saturn | 1,427 | 2.138 | 6.52651 | 18.6641 | 5.69 × 1026 | 0.764 | 432.189 | 432.139 |
Table 6: Comparative tabulation of Jupiter and Saturn masses (m), Roche's limits (aR), Inner (aG1) and outer geo synchronous orbits (aG2), the evolution factor (€=(a-aG1)/(aG2-aG1)), calculated and observed (ω /Ω.).
As given in my personal communication (http://arXiv.org/ abs/0805.1454) and in reference Sharma et al., [4] (about the evolutionary history of Mars satellite Phobos, in exactly the same manner the radial velocity expression is set up and the evolution of the semi-major axes of Jupiter and Saturn are calculated for the six sets of physically tenable birth dates as given in Table 1.
For calculating the Jupiter’s Orbital Evolution, we calculate the geosynchronous orbits (known as Clarke’s orbits also) and gravitational resonance point. Next we calculate the structure factors in the expression for radial velocity and we check if the integration of the reciprocal of radial velocity from aG1 to present semi-major axis gives the transit time of 4.56 Gy as assumed in this paper.
The ω /Ωequation, which is equivalent to lom/lod in planetary satellite dynamics, is setup:
E × X1.5 − F × X 2 / .{E →45.95926×10−16 , F→4.9227×10−21}
4.59592600000000039×10−15Χ1.5 − 4.92269999999999985×10−21Χ2….. (1)
Equation 1 is ω /Ω equation and it is tested at the present semimajor axis of Jupiter.
778.3 × 109 m to see if the calculated value of ω /Ω corresponds to the observed value.
Calculated value of ω /Ω for Jupiter at the current value of semimajor axis of Jupiter (778.3 × 109 m) is 173.726;
The observed value of ω /Ω=173.96. The calculated and observed are approximately in correspondence hence Equation 1 is correctly set up.
Geo-synchronous orbits (inner and outer Clarke’s orbits) radii are calculated by equating Equation 1 to UNITY.
The two roots of Equation 1 equated to UNITY are aG1 and aG2.
Solve [4.59592600000000039×10−15Χ1.5 − 4.92269999999999985×10−21Χ2 ==1,Χ]
{{Χ→3.78579271883727841×109},{Χ→8.71177921068034066×1011}}
Gravitational resonance point is calculated by equating Equation 1 to TWO.
Hence x2 (the point of velocity maxima) is 6.0865 × 109 m.
Now the exponent M of the structure factor is calculated by equating the first time derivative of radial velocity to ZERO at x2.
(-0.5+M) / Χ0.5 + E × (2-M)Χ - F × (2.5M)Χ1.5 /. {E → 45.95926 × 10-16, F → 4.9227 × 10-21}
First E and F numerical values are substituted in the first time derivative of radial velocity. The result is:
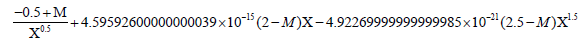
Now x2 numerical value is substituted to obtain the first derivative at velocity maxima point:
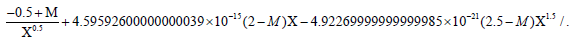
Χ→6.08652819331731542×109
The final first derivative at x2 is:
0.0000279732331734000849(2 − M) − 2.3375334095196858 × 10-6(2 − M) + 0.0000128178498819401909(−0.5 + M)… (2)
Equation 2 is equated to ZERO to obtain the exponent M:
[0.0000279732331734000849(2 − M) − 2.3375334095196858 × 10-6(2 − M) +
Solve 0.0000128178498819401909(−0.5 + M) == 0,M]
The root is: M={{M → 3.40881725753344833}}
Now constant K is determined. Through several iterations it is found that Vmax=203017 m/year gives a transit time of 4.56 Gy from aG1 to present semi-major axis.
Following Mathematica Commands are executed to determine K.
The radial velocity expression is first expressed in terms of m/year by multiplying m/sec expression by 31.5569088 × 106 seconds/ solar year and substituting the numerical values of E and F the constants of ω /ΩEquation.
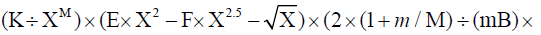 31.5569088×106 /. {E →45.95926×10−16 , F→4.9227×10−21}
31.5569088×106 /. {E →45.95926×10−16 , F→4.9227×10−21}
The result is:
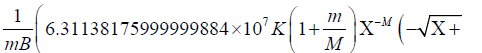 4.59592600000000039×10−15Χ1.5 − 4.92269999999999985×10−21Χ2.5))
4.59592600000000039×10−15Χ1.5 − 4.92269999999999985×10−21Χ2.5))
Next mass of Sun m0 and mass of planet Jupiter are substituted in the radial velocity expression:
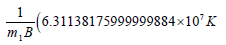
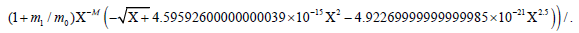 {m1 →1.9×1027,m0 →1.99×1030}
{m1 →1.9×1027,m0 →1.99×1030}
The result is:
Next numerical value of 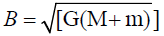 is substituted in radial velocity expression:
is substituted in radial velocity expression:
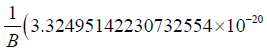
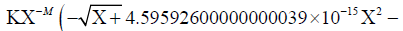 4.92269999999999985×10−21Χ2.5)) / . B → 1.152647951×1010 m
4.92269999999999985×10−21Χ2.5)) / . B → 1.152647951×1010 m
The result is:
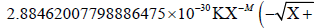 4.59592600000000039×10−15Χ2 − 4.92269999999999985×10−21Χ2.5)
4.59592600000000039×10−15Χ2 − 4.92269999999999985×10−21Χ2.5)
Next the numerical value of exponent M is substituted:
2.88462007798886475×10-30 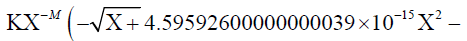 4.92269999999999985×10−21Χ2.5)) / . M → 3.40882
4.92269999999999985×10−21Χ2.5)) / . M → 3.40882
The result is:
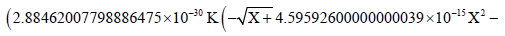 4.92269999999999985×10−21Χ2.5) / Χ3.40881999999999996
4.92269999999999985×10−21Χ2.5) / Χ3.40881999999999996
Now we have the radial velocity expression with only K unknown. To determine K we calculate the expression at x=x2:
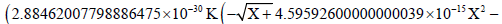 4.92269999999999985×10−21Χ2.5) / Χ3.40881999999999996 /. Χ → 6.08652819331731542 109
4.92269999999999985×10−21Χ2.5) / Χ3.40881999999999996 /. Χ → 6.08652819331731542 109
The result is Vmax expression with only K unknown:
9.97972402108637979×10-59 K
As already discussed that by several iterations we have found that Vmax should be 203017 m/year in order to achieve an Age of 4.56 Gy for Jupiter. Therefore the above expression is equated to 203017 m/yr:
Solve [9.97972402108637979×10-59 K == 203017,Κ]
The unknown K is:
{{Κ → 2.03429473170842056×1063}}
By substituting the numerical value of K we set up the complete radial velocity expression:
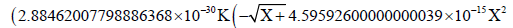 4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996 /. Κ →2.03429473170842056×1063
4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996 /. Κ →2.03429473170842056×1063
The complete radial velocity expression is:
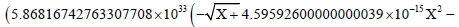 4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996 …. (3)
4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996 …. (3)
To test the correctness of the expression, the reciprocal of the radial velocity expression’s definite Integral between aG1 and present ‘a’ is calculated:
NIntegrate[
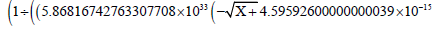 Χ2 - 4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996)), {Χ, 3.78579×109 ,778.3 10 }] … (4)
Χ2 - 4.92269999999999985×10−21Χ2.5)) / Χ3.40881999999999996)), {Χ, 3.78579×109 ,778.3 10 }] … (4)
4.56000340850643404×109 years,
The age of Jupiter comes out as assumed. It is 4.56 Gy.
Equation 4 is used to determine the orbital evolution at the given time intervals. Table 7 gives the orbital evolution of Jupiter.
| Time Before Present (B.P) | Time after the formation of Jupiter | Jupiter (m) |
|---|---|---|
| 4.56 Gy | 0 My | 3.78E+09 |
| 5 My | 8.81E+10 | |
| 10 My | 1.15E+11 | |
| 4.46 Gy | 100 M | 2.69E+11 |
| 105 M | 2.74E+11 | |
| 110 My | 2.78E+11 | |
| 4.36 GY | 200 M | 3.42E+11 |
| 205 M | 3.44E+11 | |
| 210 M | 3.47E+11 | |
| 4.26 Gy | 300 M | 3.90E+11 |
| 305 M | 3.92E+11 | |
| 310 M | 3.94E+11 | |
| 4.16 Gy | 400 M | 4.27E+11 |
| 405 M | 4.29E+11 | |
| 410 M | 4.30E+11 | |
| 4.06 Gy | 500 M | 4.57E+11 |
| 505 M | 4.59E+11 | |
| 510 M | 4.60E+11 | |
| 3.96 Gy | 600 M | 4.83E+11 |
| 605 M | 4.84E+11 | |
| 610 M | 4.85E+11 | |
| 3.86 Gy | 700 M | 5.05E+11 |
| 705 M | 5.06E+11 | |
| 710 M | 5.07E+11 | |
| 3.76 Gy | 800 M | 5.25E+11 |
| 805 M | 5.26E+11 | |
| 810 M | 5.27E+11 | |
| 3.66 Gy | 900 M | 5.43E+11 |
| 905 M | 5.43E+11 | |
| 910 M | 5.44E+11 | |
| 3.56 Gy | 1 G | 5.58E+11 |
| 1.005 G | 5.59E+11 | |
| 1.010 G | 5.60E+11 |
Table 7: Orbital evolution of Jupiter.
Similarly the radial velocity expression and the corresponding time integral equation is determined and used for calculating Saturn’s orbital evolution at intervals of 100 My . The same is repeated for different ages of Saturn.
Calculation of Saturn’s orbital evolution
For calculating the Saturn’s orbital evolution, we calculate thegeosynchronous orbits (Clarke’s orbits) and gravitational resonance point. Next we calculate the structure factors in the expression for radial velocity and we check if the integration of the reciprocal of radial velocity from aG1 to present semi-major axis of Saturn gives the transit time of 4.555 Gy as assumed in this paper. It has been assumed that Saturn is formed 5 My later or 10 My later or 15 My later or 20 My later. All these scenarios will be determined to examine the instant of 1:2 MMR crossing.
The ω /Ωequation, which is equivalent to (lom/lod) in planetary satellite dynamics, is setup:
E ×Χ1.5 − F ×Χ2 / .{E→20.15789×10(−16) , F →1.475×10(−21) )} 2.01578899999999983×10−15Χ1.5 −1.47500000000000008×10−21Χ2… (5)
Equation 5 is ω /Ω equation and it is tested at the present semi-major axis of Saturn to see if the calculated value of ω /Ω corresponds to the observed value for Saturn.
2.01578899999999983×10−15Χ1.5 − 1.47500000000000008×10−21Χ2 /. → 1427×109
432.635273982453316
The observed value of ω /Ω= 432.139. Hence Equation 5 is correctly set up.
Geo-synchronous orbits (Clarke’s orbits) radius are calculated by equating Equation 5 to UNITY.
[2.01578899999999983×10−15Χ1.5 − 1.47500000000000008×10−21Χ2 == Χ]
Solve {{Χ→6.52647141287149246×109},{Χ→1.86696927911039303×1012}}
The above two values are aG1 and aG2 of Saturn.
Gravitational resonance point is calculated for Saturn by equating Equation 5 to TWO.
[2.01578899999999983×10−15Χ1.5 −1.47500000000000008×10−21Χ2 == 2,Χ]
Solve {{Χ→1.04776529167135223×1010m},{Χ→1.86696927911039303×1012}}
Hence x2 (the point of velocity maxima) is 10.477653 × 109 m.
Now the exponent ‘M’ of the structure factor is calculated by equating the first time derivative of radial velocity to ZERO at x2.
(-0.5+M) / Χ0.5 + E (2 − M)Χ - F × (2.5 − M)Χ1.5 /. {E → 20.15789 × 10-16, F → 1.475 × 10-21}
First E and F numerical values are substituted in the first time derivative of radial velocity. The result is:
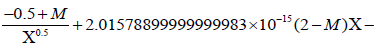 1.47500000000000008×10−21(2.5 − M)Χ1.5
1.47500000000000008×10−21(2.5 − M)Χ1.5
Now x2 numerical value is substituted to obtain the first time derivative at velocity maxima point:
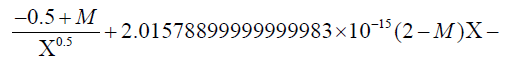 1.47500000000000008×10−21(2.5 − M)Χ1.5 / . Χ →1.04776529167135223×1010m
1.47500000000000008×10−21(2.5 − M)Χ1.5 / . Χ →1.04776529167135223×1010m
The final first time derivative at x2 corresponding to Saturn is:
0.0000211207374953290383 (2 − M) − 1.58193280467619734 × 10-6 (2.5 − M) + 9.76940234532642115 × 10-6 (−0.5 + M) ….. (6)
Equation 6 is equated to ZERO to obtain the exponent M corresponding to Saturn:
0.0000211207374953290383 (2 − M) − 1.58193280467619734 × 10-6 (2.5 − M) + 9.76940234532642115 × 10-6 (−0.5 + M) == 0, M
The root corresponding to Saturn is:
M= {{M →3.41903635715070297}}
Now constant K corresponding to Saturn is determined. Through several iterations it is found that Vmax=278027 m/year gives a transit time of 4.555 Gy from aG1 to present semi-major axis of Saturn.
Following Mathematica commands are executed to determine K.
The radial velocity expression is first expressed in terms of m/year by multiplying the m/sec expression by 31.5569088 × 106 seconds/ solar year and substituting the numerical values of E and F the constants of ω /ΩEquation.
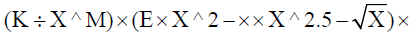
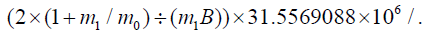 {Ε → 20.15789 × 10(-16), F → 1.475 × 10(-21)}
{Ε → 20.15789 × 10(-16), F → 1.475 × 10(-21)}
The result for Saturn is:
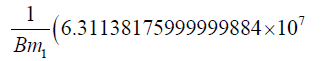
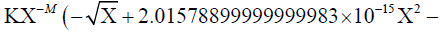 1.47500000000000008 × 10-21Χ2.5)
1.47500000000000008 × 10-21Χ2.5) 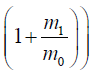
Next mass of Sun m0 and mass of planet Saturn are substituted the radial velocity expression corresponding to Saturn:
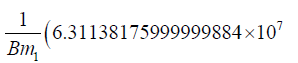
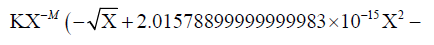
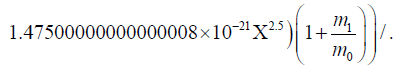 {m1 →5.69 1026 , m0 →1.99×1030}
{m1 →5.69 1026 , m0 →1.99×1030}
The result for Saturn is:
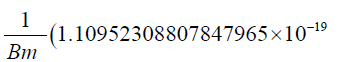
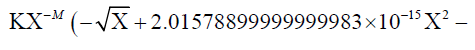
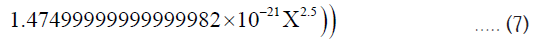
Next numerical value of 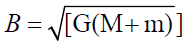 corresponding to Saturn is substituted in radial velocity expression corresponding to Saturn:
corresponding to Saturn is substituted in radial velocity expression corresponding to Saturn:
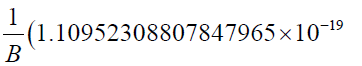
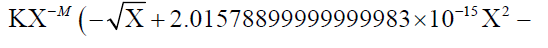 1.47499999999999982 × 10-21Χ2.5)) /. B →1.152262984 × 1010m
1.47499999999999982 × 10-21Χ2.5)) /. B →1.152262984 × 1010m
The result for Saturn is:
9.62907863469542313 × 10-30 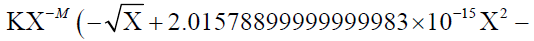 1.47499999999999982 × 10-21Χ2.5)
1.47499999999999982 × 10-21Χ2.5)
Next the numerical value of exponent M corresponding to Saturn is substituted:
9.62907863469542313 × 10-30 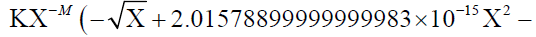 1.47499999999999982 × 10-21Χ2.5) /. M → 3.419
1.47499999999999982 × 10-21Χ2.5) /. M → 3.419
The result for Saturn is:
(9.62907863469542313 × 10-30 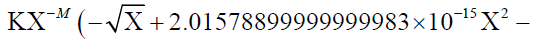 1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003
1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003
Now we have the radial velocity expression with only K unknown. To determine K we calculate the expression at x=x2 corresponding to Saturn:
(9.62907863469542313 × 10-30 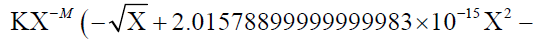 1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003 /. Χ → 10.479 × 109
1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003 /. Χ → 10.479 × 109
The result is Vmax expression corresponding to Saturn with only K unknown:
5.42542895557015292 × 10−59Κ
As already discussed that by several iterations we have found that Vmax should be 278027 m/year in order to achieve an Age of 4.555 Gy for Saturn. Therefore the above expression is equated to 278027 m/yr:
Solve [5.42542895557015292 × 10−59Κ == 278027,Κ]
The unknown K corresponding to Saturn is:
{{Κ →5.1245163044111921 × 1063}}
By substituting the numerical value of K we set up the complete radial velocity expression for Saturn:
(9.62907863469542313 × 10-30K  1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003 /. K → 5.1245163044111921×1063
1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003 /. K → 5.1245163044111921×1063
The complete radial velocity expression for Saturn is:
(4.93443704599541455 × 1034 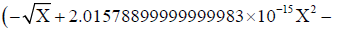 1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003
1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003
To test the correctness of the expression, the reciprocal of the radial velocity expression’s definite Integral between aG1 and present ‘a’ of Saturn is calculated:
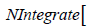
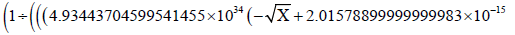 Χ2 - 1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003)), { X, 6.52647141287149246 × 109 , 1427 × 109}] …. (8)
Χ2 - 1.47499999999999982 × 10-21Χ2.5)) / Χ3.41900000000000003)), { X, 6.52647141287149246 × 109 , 1427 × 109}] …. (8)
4.55500296355435807×109
The age of Saturn comes out as assumed. It is 4.555 Gy. In this scenario it is assumed that Saturn forms 5 My after Jupiter.
Equation 8 is used to determine the orbital evolution of Saturn at 100 My interval. Table 8 gives the orbital evolution of Saturn, of Jupiter and 2:1 MMR Crossing. The 2:1 MMR crossing is identified by measuring the null point in the absolute value of [2 − Ps / Pj]. As is evident from Table 8, the null point occurs at 100 My.
| B.P | Time | Jupiter (m) | Saturn (m) | Rs/Rj | Ps/Pj | 2-Ps/Pj | |2-Ps/Pj| |
|---|---|---|---|---|---|---|---|
| 4.56 Gy | 0 | 3.78E+09 | - | - | - | - | - |
| 4.555 Gy | 5 My | 8.81E+10 | 6.53E+09 | 7.41E-02 | 0.020164 | 1.979836 | 1.979836 |
| 4.455 Gy | 105 M | 2.74E+11 | 4.34E+11 | 1.58E+00 | 1.99539 | 0.00461 | 0.00461 |
| 4.355 Gy | 205 M | 3.44E+11 | 5.56E+11 | 1.62E+00 | 2.05348 | -0.05348 | 0.05348 |
| 4.255 Gy | 305 M | 3.92E+11 | 6.40E+11 | 1.63E+00 | 2.085279 | -0.08528 | 0.085279 |
| 4.155 Gy | 405 M | 4.29E+11 | 7.05E+11 | 1.64E+00 | 2.107382 | -0.10738 | 0.107382 |
| 4.055 Gy | 505 M | 4.59E+11 | 7.59E+11 | 1.65E+00 | 2.12848 | -0.12848 | 0.12848 |
| 3.955 Gy | 605 M | 4.84E+11 | 8.06E+11 | 1.66E+00 | 2.145661 | -0.14566 | 0.145661 |
| 3.855 Gy | 705 M | 5.06E+11 | 8.46E+11 | 1.67E+00 | 2.161099 | -0.1611 | 0.161099 |
| 3.755 Gy | 805M | 5.26E+11 | 8.83E+11 | 1.68E+00 | 2.175887 | -0.17589 | 0.175887 |
| 3.655 Gy | 905 M | 5.43E+11 | 9.16E+11 | 1.69E+00 | 2.189191 | -0.18919 | 0.189191 |
| 3.555 Gy | 1.005 G | 5.59E+11 | 9.46E+11 | 1.69E+00 | 2.201958 | -0.20196 | 0.201958 |
Table 8: Orbital evolution of Saturn (Age 4.555 Gy) and MMR crossing.
Table 8 has the discrete values of time at which Jupiter and Saturn’s orbit’s semi-major axis has been calculated. Fifth Column has the ratio of Saturn’s semi major axis and Jupiter’s major axis. Sixth Column has the ratio of Saturn’s Orbital Period and Jupiter’s Orbital Period. Eighth column has the absolute value of [2 − Ps / Pj].
Ps / Pj = [Rs / Rj]3/2 ....(9)
By inspecting Table 8 we find that 1:2 MMR crossing occurs at 105 M years in the Solar history when the age difference is 5 My between Jupiter and Saturn. So we will inspect 1:2 MMR crossing for different birth dates of Saturn.
In Figure 1 we give the plot of MMR DIP Graph using Mathematica Command of List Plot.
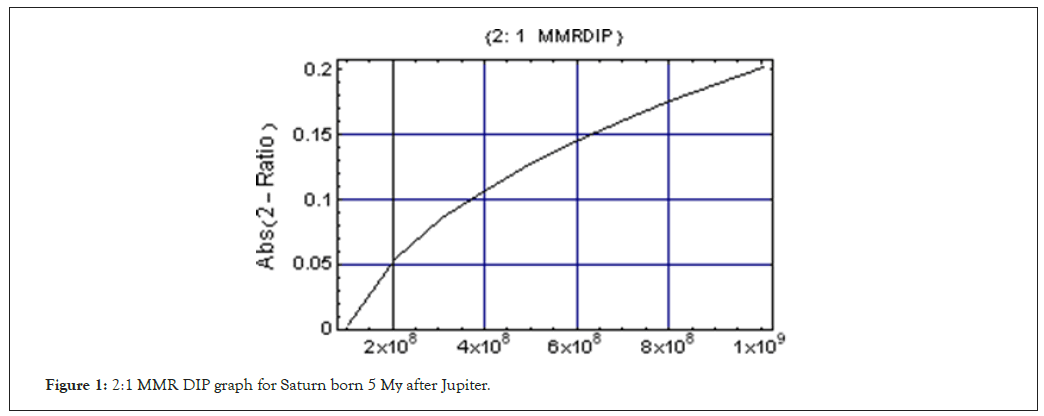
Figure 1: 2:1 MMR DIP graph for Saturn born 5 My after Jupiter.
q10 = ListPlot [{{105 × 106 ,0.00461}, {205 × 106 , 0.05348}, {305 × 106 , 0.085279}, {405 × 106 , 0.107382}, {505 × 106 , 0.12848}, {605 × 106 , 0.145661}, {705 × 106 , 0.161099}, {805 × 106 , 0.175887}, {905 × 106 , 0.189191}, {1005 × 106 , 0.201958}},
PlotJoined → True, GridLines → Automatic, Frame → True, FrameLabel → Abs (2 − Ratio), PlotLabel → {"2 :1MMR DIP"}]
Next Birth date in consideration is 10 My after Jupiter’s formation.
Table 9 gives the evolution of Jupiter and Saturn’s Orbital Evolution, Orbital Period Ratio and the absolute value of [2 − Ps / Pj].
| B.P | Time | Jupiter (m) | Saturn (m) | Rs/Rj | Ps/Pj | 2-Ps/Pj | |2-Ps/Pj| |
|---|---|---|---|---|---|---|---|
| 4.56 Gy | 0 | 3.78E+09 | - | - | - | - | - |
| - | 5 My | 8.81E+10 | - | - | - | - | - |
| 4.55 G | 10 My | 1.15E+11 | 6.53E+09 | 5.66E-02 | 1.35E-02 | 1.99E+00 | 1.986526 |
| 4.45 G | 110 My | 2.78E+11 | 4.35E+11 | 1.56E+00 | 1.95E+00 | 5.02E-02 | 0.050241 |
| 4.35 G | 210 M | 3.47E+11 | 5.56E+11 | 1.60E+00 | 2.03E+00 | -2.82E-02 | 0.028234 |
| 4.25 G | 310 M | 3.94E+11 | 6.40E+11 | 1.62E+00 | 2.07E+00 | -7.04E-02 | 0.070384 |
| 4.15 G | 410 M | 4.30E+11 | 7.05E+11 | 1.64E+00 | 2.10E+00 | -9.79E-02 | 0.097868 |
| 4.05 G | 510 M | 4.60E+11 | 7.59E+11 | 1.65E+00 | 2.12E+00 | -1.21E-01 | 0.12072 |
| 3.95 G | 610 M | 4.85E+11 | 8.06E+11 | 1.66E+00 | 2.14E+00 | -1.40E-01 | 0.139565 |
| 3.85 G | 710 M | 5.07E+11 | 8.47E+11 | 1.67E+00 | 2.16E+00 | -1.56E-01 | 0.15624 |
| 3.75 G | 810 M | 5.27E+11 | 8.83E+11 | 1.68E+00 | 2.17E+00 | -1.71E-01 | 0.171419 |
| 3.65 G | 910 M | 5.44E+11 | 9.16E+11 | 1.68E+00 | 2.18E+00 | -1.85E-01 | 0.184956 |
| 3.55 G | 1.010 G | 5.60E+11 | 9.47E+11 | 1.69E+00 | 2.20E+00 | -1.98E-01 | 0.198285 |
Table 9: Orbital evolution of Saturn (Age 4.55 Gy) and MMR crossing.
By inspection of Table 9 we find that null point of the absolute value of [2 − Ps / Pj] occurs at 200 My. So we next try Saturn born 25 My after the formation of Jupiter.
In Figure 2 MMR DIP Graph is given based on Table 9.
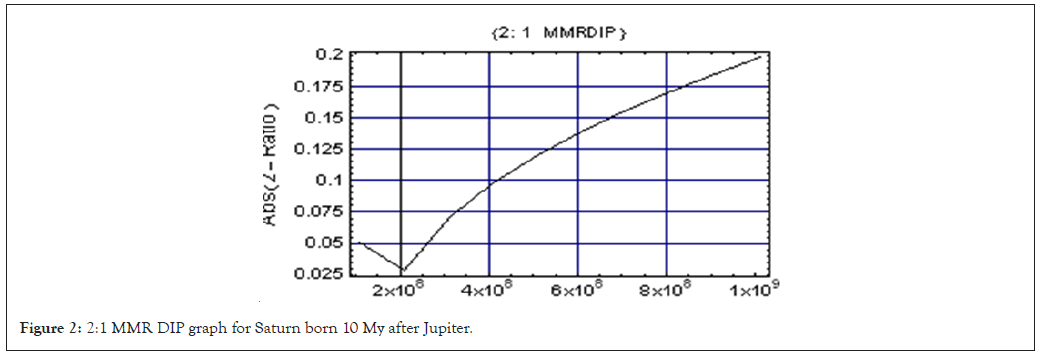
Figure 2: 2:1 MMR DIP graph for Saturn born 10 My after Jupiter.
q20 = ListPlot [{{110 × 106 , 0.050241}, {210 × 106 , 0.028234}, {310 × 106 , 0.070384}, {410 × 106 , 0.097868}, {510 × 106 , 0.12072}, {610 × 106 , 0.139565}, {710 × 106 , 0.0.15624}, {810 × 106 , 0.171419}, {910 × 106 , 0.184956}, {1010 × 106 , 0.198285}},
PlotJoined → True, GridLines → Automatic, Frame → True, FrameLabel → Abs (2 − Ratio), PlotLabel → {"2 :1MMR DIP"}]
In Table 10 the orbital evolution of Jupiter, Saturn, orbital periods ratio and MMR DIP is tabulated for the case where there is 25 My difference in the birthdays.
| B.P | Time | Jupiter (m) | Saturn (m) | Rs/Rj | Ps/Pj | 2-Ps/Pj | |2-Ps/Pj| |
|---|---|---|---|---|---|---|---|
| 4.56 Gy | 0 | 3.78E+09 | - | - | - | - | - |
| 4.535 G | 25 M | 1.63E+11 | 6.53E+09 | 4.00E-02 | 8.01E-03 | 1.99E+00 | 1.991989 |
| 4.435 G | 125 M | 2.91E+11 | 4.35E+11 | 1.49E+00 | 1.83E+00 | 1.72E-01 | 0.172344 |
| 4.335 G | 225 M | 3.55E+11 | 5.57E+11 | 1.57E+00 | 1.96E+00 | 3.62E-02 | 0.036236 |
| 4.235 G | 325 M | 4.00E+11 | 6.41E+11 | 1.60E+00 | 2.03E+00 | -2.70E+02 | 0.02699 |
| 4.135 G | 425 M | 4.35E+11 | 7.06E+11 | 1.62E+00 | 2.07E+00 | -6.68E+02 | 0.066753 |
| 4.035 G | 525M | 4.64E+11 | 7.60E+11 | 1.64E+00 | 2.10E+00 | -9.63E+02 | 0.096252 |
| 3.935 G | 625 M | 4.89E+11 | 8.07E+11 | 1.65E+00 | 2.12E+00 | -1.20E+01 | 0.119779 |
| 3.835 G | 725 M | 5.10E+11 | 8.48E+11 | 1.66E+00 | 2.14E+00 | -1.41E+01 | 0.140662 |
| 3.735 G | 825 M | 5.30E+11 | 8.84E+11 | 1.67E+00 | 2.16E+00 | -1.58E+01 | 0.157512 |
| 3.635 G | 925 M | 5.47E+11 | 9.17E+11 | 1.68E+00 | 2.17E+00 | -1.74E+01 | 0.174016 |
| 3.535 G | 1.025 G | 5.62E+11 | 9.48E+11 | 1.69E+00 | 2.19E+00 | -1.88E+01 | 0.188218 |
Table 10: Orbital evolution of Saturn (Age 4.535 Gy) and MMR crossing.
In Figure 3 the MMR DIP Graph is plotted for Saturn born 25 My after Jupiter.
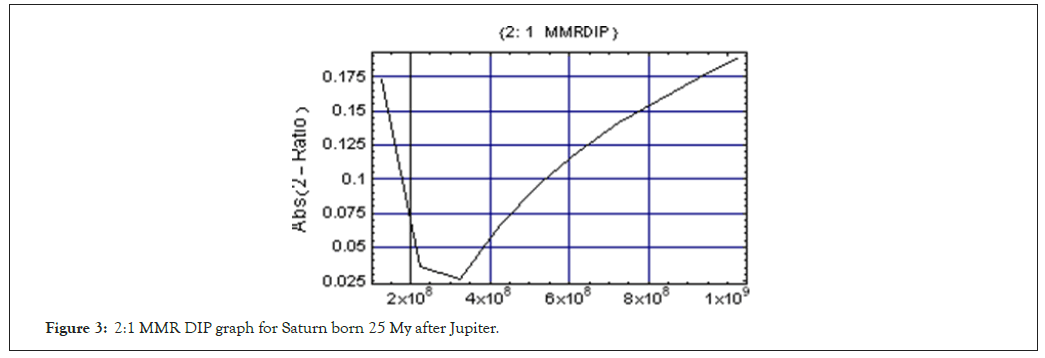
Figure 3: 2:1 MMR DIP graph for Saturn born 25 My after Jupiter.
q30 = ListPlot [{{125 × 106 , 0.050241}, {225 × 106 , 0.036236}, {325 × 106 , 0.02699}, {425 × 106 , 0.066753}, {525 × 106 , 0.096252}, {625 × 106 , 0.119779}, {725 × 106 , 0.140662}, {825 × 106 , 0.157512}, {925 × 106 , 0.174016}, {1025 × 106 , 0.188218}},
PlotJoined → True, GridLines → Automatic, Frame → True, FrameLabel → Abs (2 − Ratio), PlotLabel → {"2 :1MMR DIP"}]
The Kinematic parameters for Jupiter and Saturn are given in Table 11.
| Age | X2 (× 109 m) | M | K (N-mM+1) | Vmax (m/year) | |
|---|---|---|---|---|---|
| Jupiter | 4.56 Gy | 6.0865 | 3.40884 | 2.0343 × 1063 | 203017 |
| Saturn | 4.56 | - | - | - | - |
| 4.555 | 10.479 | 3.419 | 5.12452 × 1063 | 278027 | |
| 4.55 | 10.479 | 3.419 | 5.13029 × 1063 | 278340 | |
| 4.535 | 10.479 | 3.419 | 514706 × 1063 | 279250 |
Table 11: The kinematics parameters of the two planets.
The superposition of MMR DIP curves are given in Figure 4.
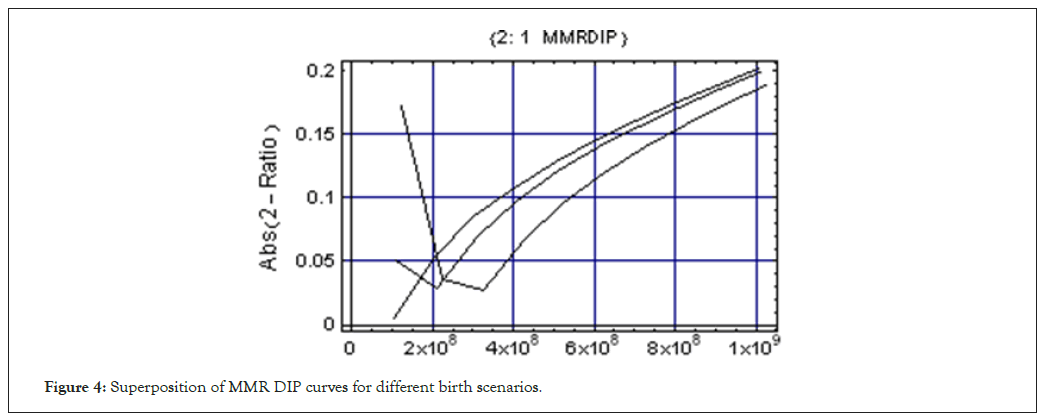
Figure 4: Superposition of MMR DIP curves for different birth scenarios.
Show[{q10,q20,q30}, Axes→True]
Late Heavy Bombardment Era corresponds to 4 Gya to 3.8 Gya. This is about 567 My to 767 My after the birth of Solar Nebula if Solar Nebula is assumed to be born at 4.567 Gya. Hence we can safely say that LHB Era occurred from 550 My to 750 My after the birth of Solar Nebula. From Table 12 it is evident that we can approach this delay in heavy meteoritic shower only by assuming that Saturn was born 25 My later than Jupiter and Jupiter was born at 4.56 Gya.
| Difference in birth dates (My) | 2:1 MMR crossing after the birth of Jupiter in My |
|---|---|
| 5 My | 100 My |
| 10 My | 200 My |
| 25 My | 300 My |
Table 12: 2:1 MMR crossing dates after the birth of Jupiter.
After examining Figures 1-3 and Table 12 we clearly see that according to our theoretical analysis MMR crossing at best must have taken place about 300 My after the birth of Jupiter. At this time 2:1 MMR crossing causes Neptune to be tossed into the outer reaches of Planetesimals disk that surround the entire Solar System called Oort’s Cloud (A band of comets believed to be in a spherical shell surrounding our Solar System and extending from 75,000 AU to 150,000 AU. www.gps.caltech.edy/~mbrown.). Neptune gravitationally scatters these planetesimals. This sends a burst of impactors throughout the entire Solar system resulting into Late Heavy Bombardment Era.
Time constraints on planetary formation does not allow Saturn to be formed any later than 25 My after the formation of Jupiter. By 30 My and the protoplanetary disk of gas and dust gets dissipated. Hence Jupiter, Saturn, Neptune and Uranus must have completed its formation within this narrow time slot. But this permits the 2:1 MMR crossing no later than 300 My. But LHB Era demands 2:1 MMR crossing in the period of 500 My to 700 My.
Under the circumstances the only explanation is the delay in response to MMR crossing. By further studies only it can be established whether there can be 200 My delay in the after effects of 2:1 MMR crossing.
From Figures 1-4 and from Table 12 we see that 2:1 MMR crossing clearly occurs after 300 My from the birth of Jupiter only when birth of Jupiter precedes that of Saturn by 25 My.
This theoretical analysis and its near correspondence with the observed data about the late heavy meteoritic shower clearly corroborates the new perspective about the birth and evolution of Solar System.
This establishes with definiteness that Jupiter was born the earliest probably 4.56 Gya and after the birth of this Gas Giant there followed the sequential formation of Saturn, Neptune and Uranus. The Jovian planets formation was completed in 30 My after Jupiter. Terrestrial planets have formed over a much longer time scale of 100 My through infrequent giant impacts. Venus and Earth was formed in rapid succession followed by Mars and Mercury. By 4.467 Gya the Solar system’s formation was completed and the last debris in the disc of accretion was completely cleared.
Then suddenly what turned on the Late Heavy Bombardment Era as late as 4.00 Gya and the entire solar system was incessantly battered for almost 200 My from 4 Gya to 3.8 Gya?
The present paper asserts that Jupiter and Saturn passed through 1:2 MMR. This caused the Neptune to be tossed into the more distant planetismal disc that surrounds the entire solar system and which is more commonly known as Oort’s Cloud. Neptune is flung on an outward migration due to 2:1 MMR resonance of Saturn and Jupiter at about 4.267 Gya. After migrating to the very edge of our Solar System, Neptune gravitationally scatters this horde of planetismals. This sends a burst of impactors throughout the entire system including our Earth and Moon and this is what has come to be known as Late Heavy Bombardment Era and which lasted for almost 200 Myr. Because of very large distances involved, the after effects of 2:1 MMR resonance was delayed by 267 My and its spill over continued for another 200 My. This is what has today come to be known as Late Heavy Bombardment Era at 4 Gy ago. This heavy bombardment continued for another 200 My persisting from 4 Gya to 3.8 Gya.
This theoretical analysis and its near correspondence with the observed data about the late heavy meteoritic shower clearly corroborates the New Perspective about the birth and evolution of Solar System.
The continued research has been made possible under Emeritus Fellowship Scheme sponsored by University Grants Commission, India. The Grant number is EMERITUS/2012-13-GEN-855/.
I acknowledge the infrastructural help given to me by the Director, IIT, Patna, in completing this paper. I acknowledge the cooperation of the staff members of IIT, Patna, who have helped me by material and moral support. I also acknowledge the moral support given by the Director, NIT, Patna, and my colleagues of NIT, Patna, in continuing my research in superannuation period. I also acknowledge the role of my D.Sc. supervisor Prof. Bhola Ishwar who mentored me through this new field of Astronomy and Astrophysics. Last of all I acknowledge the inspiration provided by George Gamow and his book ‘The story of Moon’, Carl Sagan “COSMOS” and books by Issac Asimov which laid the groundwork of this paper while I was 18 years old just introduced to General Mechanics in 2-year Physics course in my first 2 years of 5-year B.Tech. Integrated course at IIT, Kharagpur, in period 1962-1967. This paper has been almost 60 years in making.
Author collected the data regarding Length Of Day (LOD) in past epochs from popular Science books of Gamow, Carl Sagan and Issac Asimov. After receiving the press release of NASA on Silver Jubilee anniversary of Man’s landing on Moon (the historic utterances of Neil Armstrong: “Houston! This is TRANQUILITY BASE here. EAGLE has landed”.) The Press Release stated that Moon had receded by 1 m in 25 years from 20th July 1969 to 20th July 1994. Author redid the analysis of Earth Moon system and presented the result at 82nd Session of Indian Science Congress at Jadavpur University, Kolkota in 1995. Author further elaborated the Earth-Moon System Model and presented the Kinematic Model at World Space Congress, Houston, Texas, USA in 2002. In 2004 at 35th Scientific Assembly of COSPAR at Paris, France, Kinematic Model was extended to Sun-Planets system of our solar system and a new perspective on the birth and evolution of our solar system and exo-planetary systems were presented. In 2012 at 39th Scientific Assembly at Mysore, India, paper BO3-0011-12 “Iapetus hypothetical sub-satellite revisited and it reveals celestial body formation in primary centric framework”. In 2017 at CELMEC VII held at Viterbo, Rome, the Advanced Kinematic Model was presented. Subsequently a sequel paper was published titled “The Past, Present and Futuristic Earth-Moon Orbital-Globe Dynamics and its Habitability”, in Journal of Mathematical Techniques and Computational Methods, 2(1), 48-66, 2023.
There is no conflict of interest, financial or otherwise, with anybody whatsoever.
All the data is available within this paper and the references.
Citation: Sharma BK (2024) Theoretical Formulation of the Origin of Cataclysmic Late Heavy Bombardment Era based on the New Perspective of Birth and Evolution of Solar Systems. J Res Dev. 12: 267.
Received: 29-Jun-2024, Manuscript No. JRD-24-32572; Editor assigned: 02-Jul-2024, Pre QC No. JRD-24-32572 (PQ); Reviewed: 16-Jul-2024, QC No. JRD-24-32572; Revised: 23-Jul-2024, Manuscript No. JRD-24-32572 (R); Published: 30-Jul-2024 , DOI: 10.35248/2311-3278.24.12.267
Copyright: © 2024 Sharma BK. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.