Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2016) Volume 6, Issue 5
Recent theoretical studies have identified carbon-nitrogen cages are potentially stable high energy density materials. Two such C6N6H12 cages were proposed and investigated using the density functional theory comparison with two similar common cage compounds hexaazaisowurtzitane and cubane. The structure and energetic property were researched. Stability is approached in two ways: (1) stability of one isomer versus another based on the relative energy, (2) thermal stability determined by the bond breaking energies. Taking into consideration of the stability and detonation performance, two C6N6H12 cages may be candidate as potential high energy density compounds.
<Keywords: Cage; Heat of formation; Strain energy; Detonation performance; Stability
Nitrogen molecules have been the research focus in recent years as possible candidates of high energy density compounds (HEDC). A molecule Nx can undergo the reaction Nx→ (x/2) N2, a reaction that can be exothermic by more than 50 kcal/mol or more per nitrogen atom [1,2]. All-nitrogen molecules i.e., N4, N5, N6, N7, N8, N10, N12, N18, N20, N24, N30, and N36 have been studied theoretically [2-21]. There is also some research on nitrogen-rich molecules such as CxNy and OxNy species [22-26]. However, the properties of this kind of compounds are not very perfect, such as rare existence in experiments and not high stability. It has been shown that even the most stable N12 cage is of instability with regard to dissociation [27-29]. Thus, chemists often stabilize these all-nitrogen molecules with different atoms partially replacement of nitrogen atoms by sulfur atom, carbon atom or by oxygen atoms [16,17,22-26,30-32]. The advantages of these molecules are that they tend to have significant degrees of strain and high nitrogen content which will result in larger heat of formation and thus greater heat release in the detonation reactions as HEDCs. It is this point of view prompted us to research the analogy. In fact, one kind of similar C7N5H11 cages have been investigated in recent work [26]. In the current study, two C6N6H12 cages (Figure 1) with high symmetry and ring skeleton modified based on the most stable N12 cage are proposed and investigated comparison with two similar cage compounds hexaazaisowurtzitane (IW) and cubane. The structure, thermal stability, and energetic property including thermodynamic property, strain energy, heat of formation, and so on were studied through theoretical calculation for screening potential HEDCs. It is expected that our results could provide some novel insight for design and development of new HEDCs.
Gaussian 03 program package [33] was used for all calculations in this study. The geometries of C6N6H12 cages are optimized with the density functional theory (DFT) at the B3LYP level along with 6-31+G (d,p) basis set [34-36]. Vibrational analysis is performed with the absence of imaginary vibrational frequency confirming the obtained structures correspond to the true minimum on the potential energy hypersurface. Ring strain energy (SE) is a significant parameter for cage compounds. It is defined as an energy excess through a reaction in which the cyclic molecule as reactant and a strain-free counterpart as product. Various reactions have been suggested in the literature ranging from isogyric to isodesmic to homodesmotic forms [37,38]. Among them, the relatively accurate is homodesmotic schemes [39-43] in which not only the number of various bonds is conserved but also the valence environment around each atom is preserved to raise the advantage of canceling of systematic errors [44].
In the present work, the homodesmotic reactions designed for calculating the strain energies of S1 and S2 are as follows, respectively:
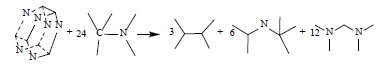 (1)
(1)
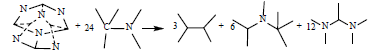 (2)
(2)
The change in energy, with the correction of zero-point vibrational energy (ZPE) of reactions is defined as the SE:
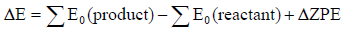 (3)
(3)
Kamlet and Jacobs provided important insight into factors that determine detonation performance [45] measured by detonation velocity and detonation pressure which is expressed by the following equation:
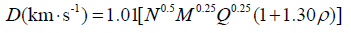 (4)
(4)
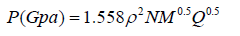 (5)
(5)
where D is detonation velocity, P is detonation pressure, ρ is the density of explosive in g·cm-3. N is the moles of gaseous detonation products per gram of explosives, M is the molecular weight of the detonation products, and Q is the heat release during the detonation reaction in cal·g-1. N, M, Q are determined based on the mot exothermic principle, that is the final detonation products are assumed N2(g), H2O(g), CO2(g), and C(g), with oxygen being used to form H2O before CO2 for C, H, O, N-containing explosives.
Pyrolysis mechanism and thermal stability can be evaluated using bond dissociation energy (BDE) [20-25,46-51] which is a measure of the strength of a chemical bond. It can be defined as the enthalpy change at 298K and 1 atm in a molecule as follows:
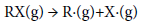 (6)
(6)
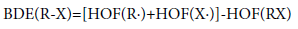 (7)
(7)
where, RX represents the neutral molecules, R· and X· represent the corresponding radical products produced by breaking the R-X bond. BDE (R-X) is the bond dissociation energy of bond R-X, HOF(X·), and HOF(RX) are the standard heats of formation for the products and reactant at 298K, respectively. However, the BDE in the present work is defined as the difference between the total energies at 0 K in the unimolecular bond dissociations. Therefore, we computed the BDE at 0 K according to the energy changes during the bond process at the B3LYP/6-31G+ (d,p) level.
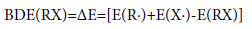 (8)
(8)
Molecular structure and electronic property
The C6N6H12 cage of S2 is modified based on the most stable N12 cage. It has four pentagons and two hexagons while S1 is composed of five hexagons as the derivative of S2. Table 1 shows the representative parameters with hexaazaisowurtzitane (IW) for comparison. It can be seen that all the C-C bonds of two C6N6H12 cages and IW are longer than the normal C-C bond (1.540Å), except for C1-C6 and C7-C8 bonds in S2, and the largest one reaches 1.611 Å for C1-C9 bond which is between two six-membered rings in S1, C1-C6 bond 1.595 Å between two heptagons in IW. Meanwhile, the C1-C6 and C7-C8 bonds in S2 which located at the junction of two five-membered rings and C3-C4 and C8-C9 bonds in IW between pentagon and hexagon are shorter than the normal C-C bond (1.540Å).
| S1 | S2 | IW | |||
|---|---|---|---|---|---|
| C1-C9 1.611 | C9-N12 1.468 | C1-C6 1.518 | C8-N2 1.449 | C1-C6 1.595 | C4-N12 1.449 |
| C2-C8 1.610 | C7-N10 1.468 | C7-C8 1.518 | C8-N10 1.530 | C3-C4 1.575 | C6-N7 1.466 |
| C4-C7 1.610 | C8-N12 1.468 | C1-N3 1.449 | C9-N4 1.491 | C8-C9 1.575 | C6-N10 1.472 |
| C1-N5 1.468 | C4-N3 1.468 | C1-N10 1.530 | C9-N5 1.491 | C1-N2 1.472 | C8-N7 1.496 |
| C1-N6 1.468 | C2-N3 1.468 | C6-N4 1.442 | C9-N10 1.531 | C1-N5 1.466 | C8-N11 1.449 |
| C9-N10 1.468 | C6-N11 1.538 | C12-N2 1.458 | C3-N2 1.481 | C9-N10 1.481 | |
| C7-N5 1.442 | C12-N3 1.458 | C3-N11 1.462 | C9-N12 1.462 | ||
| C7-N11 1.538 | C12-N11 1.584 | C4-N5 1.584 | |||
| N3-C4-N5 105.7 | N5-C4-N3 105.7 | C1-N3-C12 100.6 | N4-C6-N11 118.8 | C1-N2-C3 105.2 | C3-C4-N5 105.6 |
| N3-C2-N6 105.7 | N5-C4-C7 111.8 | C1-C6-N4 99.4 | C6-C1-N3 104.3 | C1-N5-C4 103.8 | C3-C4-N12 109.2 |
| C2-N3-C4 108.4 | C4-C7-N11 111.7 | C1-C6-N11 98.9 | C6-C1-N10 98.7 | C1-C6-N7 110.1 | C4-N12-C9 113.5 |
| C2-N6-C1 108.5 | C7-N11-C8 100.2 | N2-C8-C7 104.3 | C7-N5-N9 100.9 | C1-C6-N10 114.6 | C8-N11-C3 113.5 |
| N6-C1-N5 105.7 | N11-C8-N12 105.7 | N2-C8-N10 114.3 | N5-C9-N4 108.2 | N2-C3-C4 102.3 | N7-C8-N11 113.1 |
| C1-N5-C4 108.5 | C8-N11-C9 108.5 | N2-C12-N3 102.3 | N5-C9-N10 105.6 | N2-C3-N11 116.4 | C8-C9-N12 109.8 |
Table 1: Bond lengths (Å) and bond angles (°) of two C6N6H12 cages and IW.
Meanwhile, all the bond lengths of C-N bonds in S1 are within normal range (1.470 Å), while C-N bonds in S2 are other different case. The longest C-N bond is C7-N11 (1.538 Å) in S2 which located at the junction of pentagon and hexagon. The smallest bond angles in S1, S2, and IW are 100.2, 98.7, and 102.3°, respectively, which are smaller than the usual bonding angles of tetrahedral carbon (109.47°) and trivalent nitrogen (107.30°) but larger than 90° in cubane. It can be construed to mean that these cage structures subject to a certain degree of strain but weaker than that in cubane and they be released as an additional energy during the detonation.
Table 2 collects the frontier molecular orbital energies, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies and the energy gaps (ΔELUMO-HOMO) for S1and S2. The energy gap ΔELUMO-HOMO is an important indicator of stability for molecules. The larger the ΔELUMO-HOMO is, the more stable the molecule is during the chemical or photochemical process with electron transfer or electron leap. For example, S1 has a smaller ΔELUMO-HOMO than that of S2, indicating that S1 is less stable than that of S2 when a chemical or photochemical reaction happens.
| Isomers | EHOMO/eV | ELUMO/eV | ΔELUMO-HOMO/eV |
|---|---|---|---|
| S1 | -0.18922 | -0.01954 | 0.16968 |
| S2 | -0.23056 | -0.00926 | 0.22130 |
Table 2: Selected properties of two C6N6H12 cages.
Infrared spectrum and thermodynamic property
Infrared spectrum (IR) is not only the basic property of compounds, but also an efficient approach to identify substances. Besides, it is necessary to predict the thermodynamic properties. Therefore, it is a very important parameter. Since the DFT-calculated harmonic vibrational frequencies are usually larger than those observed experimentally, they are scaled by using a factor of 0.96 [52] which has been proved to be suitable [21-25,48,50]. Figure 2 presents the simulated IR spectrum for S1and S2. Obviously, there are four main characteristic regions in S1. The modes in 574.57 and 859.21cm-1 are associated with the C-H twisting out of plane. The peak at 713.15cm-1 is characterized to the N-H twisting out of plane. The band at 3070.77~ 3087.88cm-1 is associated with the C-H stretch. Meanwhile, there are three main characteristic regions in S2. The strongest modes in 815.07cm-1 are associated with the N-H rocking vibration. The band at 3092.17~ 3151.09cm-1 is associated with the C-H stretch. Also, there are many small peaks in S2, which can be attributable to its skeleton distortions caused by many modes of vibration from chemical bonds.
Thermodynamic properties are important parameters, i.e., standard molar heat capacity C°p,m in J·mol-1 ·K-1, entropy S°m in J·mol-1 ·K-1, and enthalpy H°m in kJ·mol-1. Based on the scaled vibrational frequencies, C°p,m , S°m , and H°m of S1 and S2 ranging from 200 to 800 K are obtained based on statistical thermodynamic principle and listed in Table 3. It can be seen that all the thermodynamic properties increase with the temperature evidently. This is because the main contributions to the thermodynamic functions are from the translation and rotation of molecules when the temperature is low; however, at higher temperature, the vibrations are intensified and therefore make more contributions to the thermodynamic properties and lead to the increase in the thermodynamic functions. In addition, the C°p,m , S°m , and H°m of S1 are generally larger than those of S2. This could be due to the fact that S1 has one more C-C bond than that of S2 while they have the same numbers of C-N bonds, resulting in more freedoms of motion in S1, i.e., translation, rotation, and vibration, thus more contributions to the thermodynamic properties for S1. The temperature-dependent relations for C°p,m , S°m , and H°m are as follows and expressed as in Figure 3.
| Compd. | Parameters | 200.0K | 300.0K | 400.0K | 500.0K | 600.0K | 700.0K | 800.0K |
|---|---|---|---|---|---|---|---|---|
| S1 | C°p,m | 92.75 | 165.82 | 234.65 | 290.61 | 334.22 | 368.51 | 396.11 |
| S°m | 301.80 | 353.05 | 410.44 | 469.06 | 526.06 | 580.26 | 631.33 | |
| H°m | 9.74 | 22.63 | 42.74 | 69.12 | 100.45 | 135.65 | 173.93 | |
| S2 | C°p,m | 84.06 | 150.38 | 216.22 | 269.34 | 310.46 | 342.49 | 368.02 |
| S°m | 298.89 | 345.32 | 397.92 | 452.12 | 505.02 | 555.38 | 602.84 | |
| H°m | 9.37 | 21.05 | 39.48 | 63.87 | 92.95 | 125.66 | 161.24 |
Table 3: Thermodynamic properties of S1 and S2 at different temperatures.
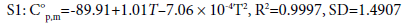 (9)
(9)
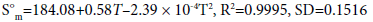 (10)
(10)
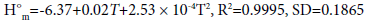 (11)
(11)
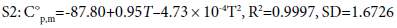 (12)
(12)
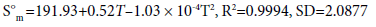 (13)
(13)
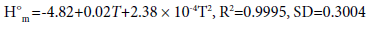 (14)
(14)
Strain energy and heat of formation
The assessment of ring strain energy in ring compounds has been a topic of major interest to the organic chemist for decades [49-58]. Studies have proved that computational results of SE at the B3LYP/6- 31G+(d,p) via homodesmotic process are reasonable [22,23,37,38,59]. For example, the SE of norbornane obtained by the homodesmotic method (63.15 kJ·mol-1) [60] is in agreement with experimental value (60.22 kJ·mol-1) [61]. In the present work, the strain energies of C6N6H12 cages are obtained by the homodesmotic reaction (1) and (2). For comparison, the following reactions are used to evaluate the SEs of hexaazaisowurtzitane and cubane, respectively:
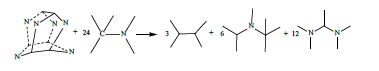 (15)
(15)
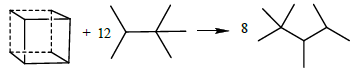 (16)
(16)
Table 4 collects the total energies (E0) and SEs of the species involved in the reactions. Obviously, S2 has a larger strain energy (3475.88 kJ·mol-1) than that of S1 (287.93 kJ·mol-1), which can be attributable to its special structures composed of four pentagons and two hexagons while S1 is made up of five hexagons. As is known, the smaller the ring is, the greater distorted the molecule is, thus, the less the strain energy becomes. Thus, it could be concluded that S1 is more stable than S2 from this point of view.
| Compd. | E0a/(a.u.) | ZPE/(a.u.) | SE/(kJ·mol-1) | HOF/(kJ·mol-1) |
|---|---|---|---|---|
| CH3NHCH3 | -135.18128 | 0.092350 | 0 | -82.98c |
| NH2CH2NH2 | -151.23042 | 0.082069 | 0 | -78.84c |
| CH3NH2 | -95.87185 | 0.064051 | 0 | -80.37c |
| CH3CH3 | -79.84164 | 0.074599 | 0 | -84.00d |
| S1 | -564.32847 | 0.21048 | 287.93 | 520.85 |
| S2 | -563.09026 | 0.18642 | 3475.88 | 3711.86 |
| IW | -564.36584 | 0.21129 | 192.16 | 425.08(319.88e) |
| cubane | -309.47990 | 0.13339 | 573.91(656.57b) | 507.91(619.98f) |
aE0 is the total energy after the correction of ZPE; bRef [62]; cObtained at the G3 level from the formation reactions: 2C(g)+3H2+N2→CH3NHCH3, C(g)+3H2+N2→NH2CH2NH2CH3, C(g)+2.5H2+0.5N2→CH3NH2; dRef [63]; eRef [37]; fRef [64]
Table 4: SEs and HOFs for C6N6H12 cages, IW, and cubane.
A key property of an energetic material that is used to assess its potential performance in a gun or warhead is its heat of formation (HOF), as it enters into the calculation of explosive and propellant properties such as detonation velocity and detonation pressure. DFT methods have been proved accurate for computing HOF through appropriate reactions [21-25,62-65]. In the present work, we calculated the HOFs of S1 and S2 by reaction (1) and (2) and hexaazaisowurtzitane by reaction (17) as well as the HOF of cubane by reaction (18) for comparison.
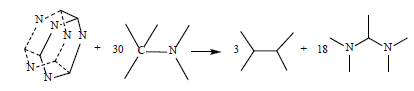 (17)
(17)
 (18)
(18)
From the data in Table 4, it can be seen that the strain energy of S2 is seven times larger than that of S1 and both of them are not only larger than those of IW either obtained at the same computational level (425.08 kJ·mol-1) or experimental value (319.88 kJ·mol-1) but also larger than that of cubane at the same computational level (507.91 kJ·mol-1). This indicates that the heat release will be gained in both of C6N6H12 cage and S2 will benefit more during the detonation.
Density and detonation characteristics
A high density is a top priority in seeking to develop new explosives. Then follow the detonation velocity and detonation pressure which are also crucial importance to an energetic material. In the present work, density was predicted from the molecular volume divided by molecular weight, while the molecular volume was obtained from the average of 100 single points molar volumes for each optimized structures. Detonation velocity D and detonation pressure P are evaluated by the Kamlet and Jacobs equation (4) and (5).
The amount of energy Q, important parameters reflecting the explosive performances of energetic materials, is commonly taken to corresponding to the total energy change per gram during the detonation. It is the negative of the total energy change:
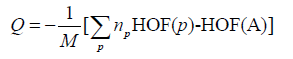 (19)
(19)
Where np is the number of moles of final product p, having molar heat of formation HOF(p), and HOF(A) is the molar heat of formation of the compound A.
The following detonation reactions were used to evaluate the detonation energy Q for two C6N6H12 isomers, IW, and cubane:
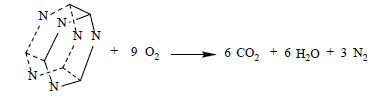 (20)
(20)
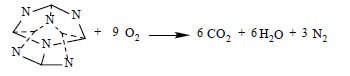 (21)
(21)
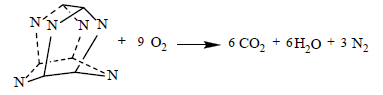 (22)
(22)
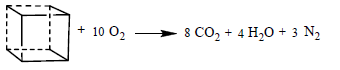 (23)
(23)
Table 5 collects the densities and detonation characteristics for the corresponding compounds. It is noted that both of S1 and S2 have larger density than that of cubane regardless of computational result (1.235 g·cm-3) obtained at the same level or experimental value (1.290 g·cm-3). The detonation velocity of S1 is slight smaller than that of S2 but still larger than that of cubane. Both of S1 and S2 have higher detonation pressure that those of IW and cubane indicating that S1 and S2 have greater power during the detonation process. The detonation energy of S1 and S2 are more negative than those of IW and cubane, implying that the title cages will release more energy during the detonation. It might seem surprising that the Q of S2 is rather negative which may be caused by its high HOF and large SE.
| Compd. | ρ/(g·cm-3) | D/(km·s-1) | P/(Gpa) | Q/(kJ·g-1) |
|---|---|---|---|---|
| S1 | 1.418 | 5.72 | 12.43 | -25.79 |
| S2 | 1.498 | 5.93 | 13.88 | -43.57 |
| IW | 1.441(1.570a) | 5.78(6.12a) | 12.84(15.24a) | -25.22 |
| cubane | 1.235(1.290b) | 3.59(3.69b) | 4.42(4.82b) | -21.20 |
Table 5: Densities and Enthalpies of combustion for C6N6H12 cages, IW, and cubane.
Thermal stability
Another important aspect of energetic materials is whether they are kinetically stable enough to be of practical interest. A good candidate HEDM should have a high stability. Thus, studies on the thermal stability are important and essential for understanding the decomposition process of the energetic materials because they are directly relevant to the sensitivity and safety of the energetic compounds during the storage or transportation.
In the present work, the stability of C6N6H12 cages is approached in two ways: (1) stability of one isomer versus another based on the relative energy, (2) thermal stability determined by the bond breaking energies. And so we can get a better understanding of the relationship between the structures and thermal stability for this king of cage compounds.
Table 6 collects the relative energies of two C6N6H12 cages obtained at the B3LYP/6-31G+(d,p) level and their composition. Obviously, S1 gets a more negative energy than that of S2, thus, S1 is more stable than S2. The primary reason may be the relative bond strength between C-C and C-N bonds. The bond energies for two bonds are 347.94 and 304.87 kJ·mol-1, respectively [66-71]. Generally, for any rearrangement of the atoms, the replacement of a C-C with C-N bond should be energetically disadvantageous by 43.07 kJ·mol-1. Compared with S2, S1 should reap the benefit for its arrangement and should be more stable by about 652.81 kJ·mol-1. Another reason may be due to their structures. S1 is composed by five hexagons while S2 is made up of four pentagons and two hexagons. As is known, the smaller the polygon is, the larger SE it subjects to. Therefore, S2 experiences more strain energy which has been verified in the section of “strain energy” and it is less stable than S1.
| Isomers | S1 | S2 |
|---|---|---|
| Bonds C-C bonds | 3 | 2 |
| C-N bonds | 12 | 11 |
| Polygons pentagons | 0 | 4 |
| Hexagons | 5 | 2 |
| Energies (kJ·mol-1) | -774.73 | 0 |
Table 6: Bond properties and relative energies of two cages.
The bond breaking energy is another important factor that related to the stability for energetic materials. The bond strength of C6N6H12 cages is evaluated by the Wiberg Bond Index (WBI) based on the NBO analysis. Often, the smaller Wiberg bond index is, the weaker bond is. Therefore, we picked out the smallest WBI of the same kind. For example, the environments of C1-C9, C2-C8, and C4-C7 in S2 consist of four C-N bonds and both of them are at the junction of two hexagons, that is, they belong to the same kind of bond. In the same way, we select C1-C6, C1-N3, C1-N10, C9-N4, and C12-N11 bonds for S2, C1-C6 and C4-N5 bonds for IW, and C1-C3 bond for cubane.
From the results in Table 7, one can find the weakest bonds for S1, S2, IW, and cubane are C2-N3, C1-N10, C1-C6, and C1-C3 with BDEs 240.14 kJ·mol-1, 134.49 kJ·mol-1, 263.67 kJ·mol-1, and 160.46 kJ·mol-1, respectively, indicating that S1, S2, and IW will break a C-N bond for the first step in the pyrolysis while it would begin with the breaking of a C-C bond for cubane. In addition, S1 has a better stability than S2 although both of them may not as stable as IW. In addition, the results in the present work also prove that the dissociation energy of C-C bond is not always larger than that of C-N bond in the cage molecules.
| C-C | C-N | |
|---|---|---|
| S1 | C1-C9 0.9203 323.12 | C2-N3 0.9883 240.14 |
| S2 | C1-C6 0.9671 170.27 | C1-N3 0.9991 259.31 C1-N10 0.9350 134.49 C9-N4 0.9710 264.96 C12-N11 0.8981 163.46 |
| IW | C1-C6 0.9266 263.27 | C4-N5 0.9585 285.28 |
| Cubane | C1-C3 0.9917 160.46 | - |
Table 7: WBI and BDE (kJ·mol-1) for C6N6H12 isomers, IW, and cubane.
On the basis of theoretical studies on two C6N6H12 cages comparison with hexaazaisowurtzitane and cubane, we can draw the following conclusions:
(1) The thermodynamic properties of two cages all increase with the temperature remarkably. S1 has generally larger C°p,m , S°m , and H°m than t hose of S2 at the corresponding temperature due to their different structure composition.
(2) The results of strain energies indicate S2 composed of more small polygons experiences much larger strain energy than S1 which may lead to the instability of S2.
(3) Both of S1 and S2 have high positive heat of formation. Thus, quite huge of energy will be released if the compounds decomposes which verifies the heat release during the detonation process. (4) The density and detonation characteristics of S1 and S2 are equivalent or slightly superior to those of hexaazaisowurtzitane and cubane, especially they have relatively negative detonation energy. (5) The results of stability suggest S1 which contains more C-C bonds are usually more stable than S2 in which C-N bonds are more than C-C bonds and also S1 is more stable with respect to bond dissociation energy. Taking the detonation performance and stability into consideration, two C6N6H12 cages may be candidate as potential HEDMs. It is hoped that the present systemic comparative investigation would be useful for molecular structural design and research of cage compounds in future.
This project is supported by the research fund of ChuZhou University under No. 2014qd039, 2015qd13, and General project of natural science research in Anhui Province (KJ2015B08).