Organic Chemistry: Current Research
Open Access
ISSN: 2161-0401
ISSN: 2161-0401
Research Article - (2017) Volume 6, Issue 2
Using the concept of three-electron bond we can represent the actual electron structure of benzene and other molecules, explain specificity of the aromatic bond and calculate the delocalization energy. Gives theoretical justification and experimental confirmation of existence of the three-electron bond. It was shown, that functional relation y=a+b/x+c/ x2 fully describes dependence of energy and multiplicity of chemical bond from bond distance.
Keywords: Benzene; Three-electron bond; Semi-virtual particle; Fermion; Entangled quantum state; Interfering universe
Chemical bond has been always a basis of chemistry. Advancement of chemical science can be considered as evolution, development of concepts about chemical bond. Aromatic bond is fundamental basis of organic chemistry. Concept of three-electron bond in benzene molecule enables to explain specificity of aromatic bond. It also becomes apparent, why planar molecules with 6, 10 etc. electrons (according to Hückel rule 4n+2) must be aromatic, and planar molecules with 4, 8 etc. electrons cannot be aromatic by definition. Description of chemical bond, that is given by quantum theory, especially in terms of method of molecular orbitals, is just a mathematical model. This model is an approximate representation of molecules and its bonds, whereas quantum-mechanical calculations of organic molecules require considerable simplifications and are extremely complicated. Concept of three-electron bond and developed mathematical relations in this work are rather simple, illustrative and give exact results of different values (bond multiplicity, chemical bound energy, delocalization energy of benzene) [1,2]. One must clearly imagine, that three-electron bond is joint interaction of three electrons with relative spins, that results in new type of chemical bond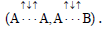 This bond type, three-electron bond, makes possible to describe real molecules of organic and inorganic compounds without invoking virtual structures, which do not exist in real terms. Using of three-electron bond before description of benzene molecule enables to determine delocalization energy of benzene in an elementary way, understand why multiplicity of С-С bond of benzene is more than 1.5 and to understand the main point of aromatic bond in general, which is appeared to be rather illustrative [3,4]. Besides, for determination of delocalization energy it is not required to select reference structures. Delocalization energy follows from the concept of aromaticity of benzene and its structure on the basis of three-electron bond. I note that the three-electron bonds to describe the benzene molecule used by Kermak WO, et al. at the beginning of the 20th century [5,6] (Figure 1).
This bond type, three-electron bond, makes possible to describe real molecules of organic and inorganic compounds without invoking virtual structures, which do not exist in real terms. Using of three-electron bond before description of benzene molecule enables to determine delocalization energy of benzene in an elementary way, understand why multiplicity of С-С bond of benzene is more than 1.5 and to understand the main point of aromatic bond in general, which is appeared to be rather illustrative [3,4]. Besides, for determination of delocalization energy it is not required to select reference structures. Delocalization energy follows from the concept of aromaticity of benzene and its structure on the basis of three-electron bond. I note that the three-electron bonds to describe the benzene molecule used by Kermak WO, et al. at the beginning of the 20th century [5,6] (Figure 1).
But since it is not taken into account the spin of electrons, have already started cyclooctatetraene problems and therefore the description of the benzene molecule by a three-electron proved unsuccessful. Using the three-electron bond with multiplicity of 1.5 and take account of the spin of each electron leads to very good results in the description of the benzene molecule and explain the aromaticity in general. With the help of three-electron bond with multiplicity of 1.5 can be represented by a real formula of many organic and inorganic molecules without the aid of virtual structures.
Results and Discussion
Supposing that the chemical bond between two atoms can be established by means of three electrons with oppositely oriented spins (↑↓↑) the structure of the benzene molecule can be expressed as follows (Figures 2 and 3).
It is interesting to point out that spins of central electrons on opposite sides have an opposite orientation (Figure 2). Now let us consider in detail the interaction of six central electrons between themselves. They will be itemized as shown in Figure 2. As the spin of electron 1 and those of electrons 2 and 6 are oppositely oriented (Figure 2) (1 (+), 2 (-), 6 (-)), electron 1 will be attracted to electrons 2 and 6 respectively. Let’s indicate that the distance between electrons 1 and 6 or 1 and 2 is equal to 1.210 Å which can be easily shown taking into account the distance between atoms of carbon in benzene to be 1.397 Å and the angle between carbon atoms amount to 120 degrees. Let us compare the distance between electrons 1 and 6 and 1 and 2 bond lengths in ethane, ethylene and acetylene [7] (Figure 3).
As we observe, the distance between central electrons 1 and 2 and 1 and 6 of the benzene molecule is approximately equal to that between carbon atoms in the acetylene molecule, therefore, the interaction between electrons 1 (+) and 2 (-) and 1 (+) and 6 (-) has to be rather considerable. Let us express the attraction with arrows. According to summing up vectors the resultant vector will be directed to the centre, which means that electron 1 under the influence of electrons 2 and 6 will move to the centre (Figures 3 and 4).
If we take a look at electron 4 we see the similar situation with it (Figure 4) and it will also move to the centre and, more importantly, its spin and that of electron 1 will be oppositely oriented, i.e., electron 1 (+) and electron 4 (-) will be attracted through the cycle. Electrons 6 (-) and 3 (+) and electrons 2 (-) and 5 (+) will interact similarly. The distance between electrons 1 and 4 in benzene is equal to 2.420 Å. It is interesting, that this distance is twice as much than distance between electrons 1 and 2, or between electrons 1 and 6 (1.210 Å ∙ 2=2.420 Å). This interaction through the cycle constitutes the essence of the delocalization of electrons, of course together with a three-electron bond [7]. Since besides the three-electron bond in the benzene molecule there is an interaction through the cycle, meaning that the benzene nucleus undergoes a kind of compression it is clear that the c-c bond multiplicity in benzene will exceed 1.5.
So, the aromatic system is a cyclic system with three-electron bonds where an interaction of central electrons through the cycle is observed. In the benzene molecule, there are three interactions through the cyclepairwise between electrons 1 (+) and 4 (-), 2 (-) and 5 (+), 3 (+) and 6 (-), as shown in Figure 5.
Carbon atoms in benzene are sp²-hybridized. The three-electron bond between carbon atoms in the benzene molecule can be represented as follows (Figure 6).
Carbon atoms in benzene have an octet equal to 8 (3+3+2=8). It should be pointed out that due to the largest distance from the atoms nuclei the central electrons of the three-electron bond are supposed to be the most mobile compared to other electrons of the three-electron bond. The interaction of central electrons with opposite spins through the cycle can easily explain why cyclobutadiene and cyclooctatetraene are not aromatic compounds (Figure 7).
As we see both in cyclobutadiene and cyclooctatetraene, electrons interacting through the cycle have the same spins and, clearly, will be repulsed, therefore there will be no interaction through the cycle and the molecule will not be aromatic. In cyclobutadiene at the expense of small distance it causes the appearance of antiaromatic properties, and in cyclooctatetraene there is a possibility of formation of non-planar molecule, where interaction of central electrons becomes impossible and molecule losing the interaction through the cycle loses also threeelectron bonds, that results in a structure, in which single and double bonds alternate.
Explanation, that cyclooctatetraene is non-aromatic, because it is non-planar and does not hold water, insomuch as dianion of cyclooctatetraene is aromatic and has planar structure [8,9] (Figure 8).
Planar X-ray crystal structure analysis determined crystal structure of potassium salt of dianion 1,3,5,7-tetramethylcyclooctatetraene [10,11]. Octatomic cycle is planar with lengths of С-С bonds nearly 1.41 Å (Figure 9).
Planar from the mentioned above, we can make a conclusion: cyclooctatetraene conforms to the shape of bath tub not because of high angular pressure (15°) at planar structure, but because by interaction through the cycle central electrons of three-electron bonds have equal spin and will push away. Thus, for energy reduction cyclooctatetraene conforms to the shape of bath tub and becomes nonplanar, that disables interaction of central electrons. Cyclobutadiene represents rectangular high reactivity diene [8]. It is also interesting to observe cyclodecapentaene (cis-isomer [10]-annulene) (Figures 10 and 11) Whereas central electrons of three-electron bonds have opposite spins, then interaction through the cycle is possible. But distances between central electrons on opposite sides, which interact through the cycle, are extremely long (4.309 Å if accept Lс-с=1.400 Å for regular decagon), angular pressure is high (24°) and that’s why stabilization at the expense of interaction through the cycle at such long distance will be low and cannot cover energy consumption for creation of planar molecule.
Cyclodecapentaene was received in the form of crystalline substance at-80°С. On spectrums 13С-NMR and ¹Н-NMR it was determined, that compound is non-planar and is olefin, that is logical on the basis of long distance between central electrons [8,12]. Lets draw our attention to the fact that in going from benzene to cyclooctatetraene and to cyclodecapentaene distance increases not only between central electrons on the opposite sides (interaction through the cycle), but also between neighboring central electrons (Figure 12).
As we can see distance between neighboring central electrons 1 and 2 in benzene makes up 1.210 Å, in regular octagon 1.303 Å, and in regular decagon 1.331 Å (almost as distance between carbon atoms in ethene molecule). That is by going from benzene to regular octagon and decagon not only angular pressure (0°, 15°, 24°) and distance between central electrons increase, which are situated on the opposite sides (2.420 Å; 3.404 Å; 4.309 Å), as well as distance between neighboring central electrons 1 and 2 (1.210 Å; 1.303 Å; 1.331 Å), that causes considerable weakening of interaction through the cycle in regular decagon. That’s why regular hexagon (benzene) is ideal aromatic system [13-17]. As angular pressure is equal to zero, distances between central electrons both neighboring and situated on the opposite sides are minimal (accordingly 1.210 Å and 2.420 Å) i.e., interaction through the cycle will be maximal. By going to regular decagon these advantages will be lost. That’s why cyclodecapentaene is olefin [18,19].
us note for comparison that if we take Lc-c=1.400 Å for the planar cyclooctatetraen, we will have L(1-5)=3.380 Å, L(1-2)=L(8-1)=1.293 Å which vary just slightly from the above mentioned distances between the central electrons at Lс-с=1.410 Å [20-25].
By means of the interacti on through the cycle together with the three-electron bond, three aromaticity of coronen, [18]-annulene, naphthalene and other organis substances can be explained (see conclusion).
Now let’s pass to the definition of delocalization energy of benzene. It is easy to show, that relation multiplicity=f(L) and Е=f(L), where multiplicity is multiplicity of bond, L – length of bond in Å, Е – energy of bond in kj/mole will be described by function y=a+b/x+c/x² for any types of bond (C-C, C-N, C-O, C-S, N-N, N-O, O-O, C-P).
We shall consider ethane, ethylene and acetylene to be initial points for the c-c bond. For lengths of bonds let us take the date [7,26]:
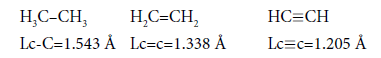
As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3. For energies of bonds let us take the date [7]:
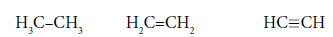
Ec-c=347.9397 kj/mole Ec=c=615.489 kj/mole Ec≡c=8.12.278 kj/mole
The given bond energies (according to Pauling L) are bond energy constants expressing the energy that would be spent for an ideal rupture of these bonds without any further rebuilding of the resulting fragments. That is, the above-mentioned energies are not bond dissociation energies [27,28].
Having performed all necessary calculations, we obtain the equation:
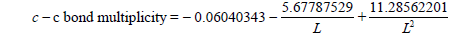 (1)
(1)
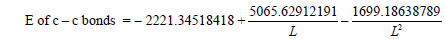 (2)
(2)
From these equations we find:
c–c graphite multiplicity (L=1.42 Å)=1.538 ≈ 1.54
Ec–c benzene (L=1.397 Å)=534.0723 kj/mole
Ec–c graphite (L=1.42 Å)=503.3161 kj/mole
Being aware that the benzene has the three-electron bonds and also the interaction through the cycle, we can calculate the interaction through the cycle energy (Figure 13) [29-32]. For this purpose, we have to determine the energy of the “clean” three-electron bond, that is of the bond with a 1.5 multiplicity and to do that we shall solve the equation:
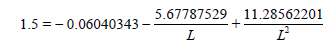 (3)
(3)
from the equation, we find L=1.42757236 Å.
So, if the benzene molecule had a “clean” three-electron bond with a 1.5 multiplicity the c-c bond length would be L=1.42757236 Å.
Now let us determine the energy of the “clean” three-electron bond with a 1.5 multiplicity knowing its length L=1.42757236 Å:
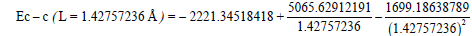
Ec-c (L=1.42757236 Å)=493.3097 kj/mole
Taking into account that the benzene c-c bond energy with a 1.658 multiplicity is equal to Ec-c benzene=534.0723 kj/mole, the difference will make:
ΔE=534.0723 kj/mole-493.3097 kj/mole=40.7626 kj/mole.
40.7626 kj/mole is the energu of interaction through the cycle per one c-c bond [33-35]. Therefore, the energy of interaction through the cycle will be two times higher:
E1=40.7626 kj/mole ∙ 2=81.5252 kj/mole (19.472 kcal/mole)
It is clear that the three interactions through the cycle present precisely the working benzene delocalization energy which is:
E=3E1=3 81.5252 kj/mole=244.5756 kj/mole (58.416 kcal/mole)
It is also possible to calculate the benzene molecule energy gain in comparison with the curved cyclohexatriene (let us assume that energy of C-H bonds in these molecules is similar) [36-39]. For this we calculate the sum of energies of single and double c-c bonds in cyclohexatriene:
E2=3Ec–c+3Ec=c=2890.286 kj/mole
The energy of six benzene c-c bonds with a 1.658 multiplicity is equal to:
E3=6 534.0723 kj/mole=3204.434 kj/mole
Therefore, the gain energy of benzene compared to cyclohexatriene will amount to:
E=E3–E2=3204.434 kj/mole–2890.286 kj/mole=314.148 kj/mole (75.033 kcal/mole).
Experimental
Let’s show more detailed calculation of ratios for our mathematical relations. Let’s consider relation Multiplicity=f(L) and E=f(L) for С-С bonds, where multiplicity is multiplicity of bond, L- length of bond in Å, Е - energy of bond in kj/mole (Figure 14).
As initial points for the given bonds we will use ethane, ethene and acetylene.
For the length of bonds let us take the findings [7]:
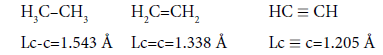
As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3. For the energy of bonds let us take the findings [7]:
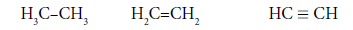
Ec-c=347.9397 kj/mole Ec=c=615.489 kj/mole Ec ≡ c=812.278 kj/mole
If we have two variants and we received the set of points and we marked them on the plane in the rectangular system of coordinates and if the present points describe the line equation y=ax+b that for choose the coefficients a and b with the least medium-quadratic deflection from the experimental points, it is needed to calculate the coefficients a and b by the formulas:
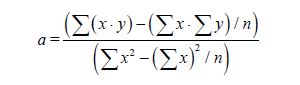 (4)
(4)
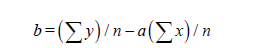 (5)
(5)
n-the number of given values x or y.
If we want to know how big the derivative is, it is necessary to state the value of agreement between calculated and evaluated values y characterized by the quantity:
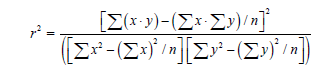 (6)
(6)
The proximity of r2 to one means that our linear regression coordinates well with experimental points [40].
Let us find by the method of selection the function y=a+b/x+c/x2 describing the dependence multiplicity=f(L) and E=f(L) in best way, in general this function describes this dependence for any chemical bonds.
Let us make some transformations for the function y=a+b/x+c/x², we accept
X=1/x,
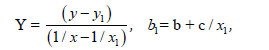
Then we’ll receive: Y=b1+cX, that is the simple line equality, then
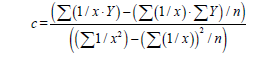 (7)
(7)
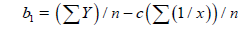 (8)
(8)
n–the number of given value Y.
Let us find a from the equality: Σy=na+bΣ(1/x) +cΣ(1/x2),
when n=3.
Let us find now multiplicity=f(L) for C─C, C═C, C≡C.
Let us find from the equation:
Multiplicity C−C (ethane)=1. Multiplicity C═C (ethylene)=2.
Multiplicity C≡C (acetylene)=3.
Multiplicity C−C (graphite) (L=1.42 Å) =1.538 ≈ 1.54.
Multiplicity C−C (benzene) (L=1.397 Å) =1.658.
As we can see the multiplicity C−C of benzene bond is 1.658 it is near the bond order of 1.667 calculated by the method MO [8].
It should be noted that the а, b, с coefficients for this y=a+b/x+c/ x2 function in case of using three pairs of points (х1, у1), (х2, у2) і (х3, у3) are defined explicitly; actually, they (the coefficients) are assigned to these points. In that way, we find these coefficients for working further with the equation. For making certain that this dependence y=a+b/x+c/ x² describes well the multiplicity=f(L) and E=f(L) functions it will take only to perform correlation for four or more points. For example, for the dependence multiplicity=f(L) for C-C bonds we should add a fourth point (Lc–c=1.397 Å, Multiplicity=1.667) and obtain an equation with r2=0.9923 and the coefficients а=- 0.55031721, b=- 4.31859233, с=10.35465915 [41,42].
As it is difficult, due to objective reason, to define four or more points for the Multiplicity=f(L) and E=f(L) equations for a separate bond type, we will find the а, b, с coefficients using three points (as a rule they are the data for single, double and triple bonds). The dependences obtained in such a way give good results as regards the bond multiplicity and energies [43,44].
We’ll find the dependence E=f(L) for the C−C bonds
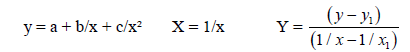

As usual:
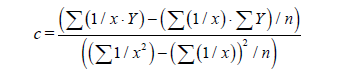 (7)
(7)
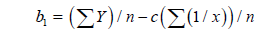 (8)
(8)
n–the number of given value Y.
Let us calculate a from the equation Σy=na+bΣ(1/x) +cΣ(1/x2), (9)
when n=3.
Conclusion
As we can see, three-electron bond enables to explain aromaticity, find delocalization energy, understand aromatic bond’s specificity. Aromatic bond in benzene molecule is simultaneous interaction of three pairs of central electrons with opposite spins through the cycle. But whereas central electrons are the part of three-electron bond, then it is practically interaction of six three-electron bonds between themselves, that is expressed in three interactions through cycle plus six three-electron bonds. We shouldn’t forget in this system about important role of six atom nucleuses, around which aromatic system is formed. Properties of nucleuses especially their charge will influence on properties of aromatic system.
Finally, postulates of the three-electron bond theory (TBT) can be presented:
• A chemical bond between two atoms may be established by means of three electrons with oppositely oriented spins (↑↓↑).
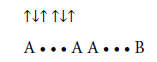
• The electron shell of each atom in the stable molecule, ion, and radical should have such a number of electrons which corresponds to the octet. A deviation from the octet results in an instability of a particle.
• The state of the three-electron bond is determined by the octet rule.
• The number of electrons participating in the chemical bond should be maximal and it’s then that the energy of the system will be minimal. Taking into consideration para 5 and 2.
• In the course of establishing of the chemical bond electrons (their spins) are located in such a way that enables the interaction (attraction) to be maximal.
• The aromatic bond is a three-electron bond in flat cyclic systems with a specific interaction of electrons through the cycle.
It is easy to show, that using three-electron bond one can explain paramagnetization and structure of oxygen molecule, structure of carboxylate anion, ozone, naphthalene and other organic and non organic compounds. Let’s bring for the example structures of some compounds in terms of three-electron bond (Figures 15-19).
It is interesting to note extreme symmetry of structures of naphthalene, anthracene, coronene and [18]-annulene, that is typical for the majority of aromatic compounds in general.
By the example of [18] annulene it is possible to illustrate interaction through the cycle of central electrons of three-electron bonds. Interacting through the cycle, it shifts to the centre in the direction of inner atoms of hydrogen thus increasing electron density within the cycle and decreasing outside the cycle. And that’s why outside protons (12 Н) will give signals in the area of weaker field (reduction of electron density), and inner (6 Н) will give signals in the area of stronger field (increase of electron density). Thus, this is observed in reality [13]. It also should be noted that inner protons bracing central electrons strengthen interaction through the cycle, and so stabilize aromatic system. But interaction through the cycle is decisive.
If aromatic system does not have inner protons, then outside protons will give signals in the area of weaker field (one of the features of aromatic compounds).
It is clear that in case of antiaromatic systems when there is no interaction (attraction) through the cycle, because central electrons have similar spins and push away, change in electron density in the centre of the cycle and outside the cycle will be reverse to aromatic systems.
Further we will continue demonstration of construction of organic and inorganic compounds (Figures 19-51).
As we can see with the help of three-electron bond structures of abovementioned molecules and ions are described simply and obviously by one structure, which represents the real distribution of electrons (electron density) in molecules (ions).
Author knowingly did not consider a question about kinds of forces that make electrons to attract with opposite spins, because it is a subject of a separate consideration. All the more so, because based on famous postulate (attraction of two electrons with opposite spins) concept of localized chemical bond follows. Explaining aromatic bond in benzene molecule, interaction of central electrons is strange on such long distances (2.420 Å). But taking into account, that electrons can show wave-like behaviour and shift to the center of benzene cycle under the influence of neighbouring central electrons, this interaction looks very truly.
The fact of the distance between the graphite layers being 3.35 Å (the С-С bond length inside the layer making 1.42 Å) [14] may serve as an indirect confirmation of the possibility of interaction of the electrons through the cycle in benzene. This causes a weak bond between the layers and, as a result, the ability of the layers to shift relative to each other. Since the distance between the central electrons in benzene is less and makes 2.420 Å (in case of an interaction through the cycle), we should expect a stronger interaction.
It is clear that, by increasing of cycle, distance between central electrons (both neighboring and through the cycle) will increase, and that’s why interaction energy through the cycle will decrease, and by certain distance benefit from aromaticity of system will be lower, than energy consumption for creation of planar equilateral polygon (as in the case of cyclodecapentaene). Therefore, existence of large aromatic monocycles will depend on relation of these two values.
With the help of equations E=a+b/L+c/L2 and multiplicity=a+b/ L+c/L2 we can analyze different types of chemical bonds, calculate their multiplicity and energy on the basis of experimental data about bonds distances. The Tables 1 and 2 show the, b and c coefficients for these equations for the bonds prevailing in the organic chemistry (C-C, C-O, C-N, C-S, N-N, N-O, O-O). The coefficients have been calculated similarly to the С-С bonds. Using them it is possible to calculate the bonds multiplicity and their energy (bond energy constants) for the most part of organic molecules, both aromatic and non-aromatic ones. It makes it possible to calculate the aromatic compounds delocalization energy.
| Type of bond | a | b | c |
|---|---|---|---|
| C-C | -0.06040343 | -5.67787529 | 11.28562201 |
| C-O | 26.03252883 | -72.46498138 | 52.43899244 |
| C-N | 0.63817306 | -7.56455294 | 11.91384503 |
| C-S | 55.33256579 | -198.81807222 | 181.87538814 |
| N-N | 0.96407492 | -6.68791795 | 9.79339013 |
| N-O | 46.00756377 | -123.75637485 | 84.79763896 |
| O-O | 23.89786759 | -66.85172754 | 48.79304255 |
| C-P | 28.76548555 | -109.46128312 | 107.52805439 |
Multiplicity - bond multiplicity; L – bond length in Å.
Table 1: Multiplicity=a+b/L+c/L² equation coefficients for some types of bonds.
| Type of bond | a | b | c |
|---|---|---|---|
| C-C | -2221.34518418 | 5065.62912191 | -1699.18638789 |
| C-O | 11420.81052442 | -31359.17576343 | 22207.04265404 |
| C-N | -2332.69568587 | 4450.61712191 | -866.48412671 |
| C-S | -27772.64385690 | 90244.55278987 | -71414.57485742 |
| N-N | 7067.14065437 | -20274.81508318 | 14878.53765631 |
| N-O | -6564.31416262 | 15895.54907490 | -8769.11638979 |
| O-O | 10590.40848780 | -29935.02909385 | 21430.93279023 |
E – bond energy in kj/mole; L – bond length in Å
Table 2: E=a+b/L+c/L² equation coefficients for some types of bonds.
It is also possible to calculate the real molecules energy gain compared to their classic structures. To do this, it is necessary to subtract the total of the classic structure bond energies from the total of the real structure bond energies (the bond energy is calculated with the E=a+b/L+c/L2 equation). Let us illustrate the above taking the urea molecule as an example (leaving out of consideration the N-H bonds):
Classic structure Real structure

LC-N=1.33 Å, LC-O=1.27 Å (14)
Multiplicity C−N=1 Multiplicity C−N (L=1.33 Å)=1.686
Multiplicity C−O=2 Multiplicity C−O (L=1.27 Å)=1.486
EC-N=291.834 kj/mole [7, с.116] ЕC-N (L=1.33 Å)=523.790 kj/mole
EC-O=728.538 kj/mole (for R2C=O) [7, с.116] EC-O (L=1.27 Å) =496.940 kj/mole
E1=EC-O+2EC-N=1312.206 kj/mole E2=EC-O+2ЕC-N=1544.520 kj/mole
ΔE=E2-E1=1544.520 kj/mole - 1312.206 kj/mole=232.314 kj/mole
So, the energy gain for a real urea molecule (with three-electron bonds) as compared to the classic structure makes 232.314 kj/mole (55.487 kcal/mole). Calculations for other molecules may be done in the same way.
This example illustrates why the three-electron bonds appear at all: it proves to be that the three-electron bonds are “more poor” by energy and formation of three-electron bonds is energetically more advantageous. The energetic advantageousness is also the reason of the deviation of the multiplicity of the three-electron bonds from 1.5 which takes place due to either the interaction of the three-electron bonds among themselves (for example, in the benzene molecule) or the interaction of the three-electron bonds with the unpaired electrons located in atoms making the bond (urea molecule). Cases are possible when the bond multiplicity is changed due to the simultaneous influence of the above-mentioned effects.
It should be also noted that the octet rule holds true in threeelectron bond structures. Thus, in the urea molecule the three-electron bond electrons interact partially with the unpaired electrons located in the atoms of oxygen and nitrogen. As a result, the three-electron bond electrons do not fully belong to the carbon atom and so the carbon atom octet makes 8 and not 9 (one should not also forget that the electronegativity of the atoms of oxygen (3.5) and nitrogen (3) is higher than the electronegativity of the atom of carbon (2.5)).
Generally, the octet rule defines the state of the three-electron bond, that is, the distribution of the electrons, the energy of their interaction with each other and other unpaired electrons, the fact and the extent of belonging of the three-electron bond electrons to one or another atom.
And finally, here are the values of the a, b, c coefficients in the Tables 1 and 2 for the Multiplicity=f(L) and E=f(L) equations.
Results and discussion
Three-electron bond in benzene is classic, “direct”, along the axis of the bond, but not in the form of “banana bond” [1]. Due to real interaction through the cycle the bond should deviate slightly from the axis, possibly by 0,1 Å - 0,2 Å, somewhat shift a little to the centre of the cycle. This shift is very slight as compared to “banana bond”.
Let us consider the picture of the molecule of pentacene (Figures 52 and 53) [15]:
Using an atomic force microscope (AFM), it is possible to obtain such photos of molecules and actually to study individual molecules and their bonds; and this particular is needed to determine the presence of the three-electron bond. Molecule of pentacene is the most representative, see photos where the displacement of the chemical bond (or rather the bond path) to the centre of the extreme cycles is clearly shown, which should be observed according to the three-electron bond theory (TBT) and the interaction through the cycle.
Formulae of naphthalene and anthracene are presented at [1] according to the TBT. The molecule of pentacene will have a similar structure according to the three-electron bond theory. Displacement of the chemical bond in the inner cycles of pentacene cannot be detected at the photo, which is logical taking into account the interaction of central electrons of the three-electron bond of inner cycles, because neighbouring central electrons act in opposite directions; so, the shift to the centre of cycles is minimal or absent.
Distribution of the intensity of chemical bond in pentacene visible in the photo can be logically explained by addition of electron densities, or broadly speaking by addition of the number of electrons involved in chemical bond. Electron density near the carbon atom is not less than in the centre of the chemical bond, so there is no protrusion of the centre of the chemical bond to the centre of the cycle (regardless of the presence of three-electron bond), which is understandable considering two three-electron bonds near the carbon atom, and therefore two neighbouring electrons with opposite spins will interact with each other.
We shall see no protrusion of the centre of the chemical bond to the centre of the cycle in similar photos of antiaromatic systems. The whole image should be similar to the image of pentacene but with a shift of the chemical bond “out of the cycle” (Figure 54).
If one considers the following molecules the following conclusions can be drawn [16] See photo Reactant 1-it is clearly shown how the triple acceptor bond pulls electron density from the benzene ring, and thus the chemical bonds of the corresponding carbon atoms will not be (or too much lesser extent will not be) drawn to the centre of the benzene cycle or so to speak “will neither bend no strain”, as we can see in the photo.
See photo Product 2-it is clearly shown two benzene nuclei and one naphthalene nucleus. The situation is repeated where the displacement of chemical bonds (three-electron bonds) to the centre of cycles is possible; it occurs and can be clearly seen in the photo. Where interaction (pumping) of electron density occurs in the result of conjugation with double bonds, we shall see no shift of the chemical bond to the centre of the cycle. Therefore, the displacement of chemical bonds of outer sides of benzene and naphthalene is clearly visible, however this effect is not observed for inner sides. See photo Product 3-it is similar to the Product 2, we just have three benzene nuclei, and the shift of chemical bonds of outer sides of benzene rings is clearly visible, however this effect is not observed for inner sides involved in conjugation.
Analysis of images made in techniques of atomic force microscopy (AFM) of high resolution in pentacene and other aromatic systems shows that according to predictions, aromatic three-electron bond is deflected to the centre of aromatic nuclei, which clearly confirms the fact of existence of three-electron bond in benzene, pentacene and other aromatic systems. It also confirms the existence of this bond in carboxylate anions and other similar ions and molecules.
AFM images of benzene can be presented on the basis of pentacene image, and if it exists, or if it is received at the appropriate resolution, it will be another confirmation of real existence of the three-electron bond.
There is no doubt that AFM images of cyclobutadiene (planar) and cyclooctatetraene (planar) or of any other planar antiaromatic system, when received at the appropriate resolution, will be another confirmation of the interaction through the cycle in aromatic and antiaromatic systems. It should be noted that the deviation of chemical bond in antiaromatic systems will be “from the cycle”, similarly to pentacene, but in the opposite direction.
But there is a nuance as for antiaromatic systems: an antiaromatic system (system of nuclei) should be planar in order to have the interaction through cycle [1]. If the system is not planar, it will be a transition into the “bath” in cyclooctatetraenyl (four double bonds), a transition into the diradical in cyclobutadiene (double bond and two unpaired electrons, the nuclei system shall be planar and not a square). Then the AFM image shall show the appropriate structure, ie double bonds plus unpaired electrons in cyclooctatetraene and cyclobutadiene.
Therefore, to obtain AFM images of antiaromatic cyclobutadiene and cyclooctatetraene, it is necessary to consolidate their atoms on a special matrix for achieving a perfect planarity of the system, and only then to pick AFM images of appropriate resolution, if it is possible. Undoubtedly, this AFM image will confirm the interaction of threeelectron bonds through the cycle.
Now the question is how to explain the existence of the threeelectron bond in benzene and other molecules and ions from the point of view of quantum theory. It stands to reason that any placement of three electrons on the same atomic or molecular orbital is out of the question. Therefore, it is necessary to lay the existence of three-electron bond in molecules in reality as an axiom. In this case the three-electron bond in benzene can be actually considered a semi-virtual particle. A real particle, such as an electron, exists in the real world for indefinitely long time. Virtual particles exist for the time which is insufficient for experimental registration (strong interactions in atomic nuclei). So, we shall call the three-electron bond which really exists for indefinitely long time only in molecules and ions a semi-virtual particle.
The three-electron bond as a semi-virtual particle has certain characteristics:
Its mass is equal to three electronic masses, its charge is equal to three electronic charges, it has half-integer spin (plus, minus 1/2) and a real spatial extension. That is, our semi-virtual particle (the three-electron bond) is a typical fermion. Fermions are particles with half-integer spin; they follow the Fermi-Dirac statistics, and have appropriate consequences, such as the Pauli Exclusion Principle etc. An electron is a typical fermion, and therefore such distribution in atomic and molecular orbitals is accepted (calculated).
It follows that the three-electron bond in benzene is a real fermion in benzene, so quantum calculations can be extended to the molecule of benzene (and other systems) with the use of corresponding fermion (i.e., three-electron bond as a particle) instead of the electron in calculations. Then everything shall be made as usual: the Pauli Exclusion Principle, distribution in MO, binding and disintegrating MO, etc.
Then, there will be three fundamental interactions (between fermions) in chemistry:
electron - electron;
electron - fermion-three-electron bond;
Conclusion
Construction of diagrams showing how electrons gravitate (in explaining the interaction through the cycle, etc.) is an attempt to explain the quantum interaction of electrons by using methods of classical chemistry [1]. It is clear that electrons do not gravitate towards each other (gravitational interaction is neglected), but on the contrary, if they gravitate, a force should exist, as well as an equation for the calculation of this force.
In nature, there are only four fundamental interactions:
1. Gravity.
2. Electromagnetic (most important for chemistry).
3. Strong.
4. Weak.
With neglect of gravitational interaction, it is only electromagnetic interaction and broadly speaking, Coulomb attraction and repulsion in the molecule (or rather between electrons and nuclei).
Quantum mechanics defines what such a chemical bond. Without quantum mechanics, it is impossible. Classical concepts to explain what the chemical bond is impossible (and this despite the existence of four fundamental interactions). It is obvious that when the chemical bond formation quantum effects are important. That is, to form a chemical bond is not enough to have two specific atoms with unpaired electrons and the four fundamental interactions, but still need these two atoms placed at a certain distance where quantum effects “help” form a chemical bond. Without quantum effects, these baselines (atoms and fundamental interactions) is not enough to form a chemical bond. It is obvious that when the chemical bonds forming, important not only the properties of atoms and fundamental interactions but also the structure of the space-time at distances of several angstroms (scale chemical bond). Quantum effects of the space-time begin to affect the interaction of atoms (the house begins to affect the interaction between residents), without it, explaining the formation of a chemical bond is impossible.
Results and Discussion
The interaction of two three-electron bonds in a molecule of benzene at a distance of 2.42 Å (on opposite sides) can be explained if we consider these two three-electron bonds as two particles (two fermions) in an entangled quantum state [4-11]. That is, these two fermions are in an entangled quantum state. Quantum entanglement is a quantum mechanical phenomenon, in which the quantum states of two or more fermions or bosons prove to be interconnected [17-21]. And surprisingly, this interconnection remains at virtually any distance between the particles (when there are no other known interactions). It should be realized that the entangled quantum system is in fact an “indivisible” object, a new particle with certain properties (and the particles of which it is composed should meet certain criteria). And most importantly, when measuring the spin (or other property) of the first particle we will automatically unambiguously know the spin (property) of the second particle (let’s say we get a positive spin of the first particle, then the spin of the second particle will always be negative, and vice versa). Two particles in an entangled state prove to be bound by an “invisible thread”, that is, in fact, they form a new “indivisible” object, a new particle. And this is an experimental fact.
As for the benzene molecule [1], if we consider the interaction of all six three-electron bonds as an entangled quantum state of six fermions (three-electron bonds), then the definition of the spin of one of the fermions automatically implies the knowledge of all the spins of the other five fermions, and in closer inspection it means the knowledge of the spins of all 18 benzene electrons that form all the six C-C bonds. In fact, on this basis, the benzene molecule can be used to study the entangled quantum states of electrons (fermions).
One can realize that the interaction of three-electron bonds in a molecule of benzene at a distance of 2.42 Å is significant on the basis of the fact that the bond length in a molecule of iodine (I-I) is about 2.66 Å. Therefore, it is reasonable to assume that the energy interaction of the three-electron bonds (or central electrons) at distances between them of 2.42 Å will be significant.
In addition, the length of chemical bonds in the general case is in the approximate range of 0.74 Å-3.5 Å. The value of 3.5 Å, in principle, restricts the existence of large monocyclic aromatic systems such as of cyclodecapentaene.
Since the distance between the opposite bonds is equal to 4.31 Å, i.e., there is no significant interaction between the three-electron bonds (or electrons located on opposite sides of the cycle) and thus there won’t be stabilization of the cycle because the distance is more than 3.5 Å, that is longer than the “longest chemical bond” [1]. Without this interaction energy, it will be impossible to stabilize a large monocyclic aromatic system, in which the cyclic strain will substantially increase.
In other systems such as naphthalene, anthracene, tetracene, pentacene, and the like, the longest interaction between two threeelectron bonds of different cycles (longer than 3.5 Å) will also be insignificant in terms of formation of a chemical bond [1].
Three-electron bonds will exist in such systems (system stabilization due to of the core of six-membered rings), but there will be no significant interaction between specific bonds over long distances (in energy terms). But this does not mean that these three-electron bonds will not interact in any way. Quite the contrary, they will certainly interact, and this interaction will lead to the formation of an entangled quantum state, which in fact will determine the type of the electron spin (or the three-electron bond). Moreover, in general, in the twoelectron chemical bond, the electrons can also be regarded as being in an entangled quantum state, which actually determines their spins.
The fact that electrons during the formation of chemical bonds are in an entangled quantum state, is very important for chemistry and quantum mechanical bond calculations. For example, when calculating the twO-electron chemical bond of a hydrogen molecule, it will no longer be necessary to consider the movement of two electrons in general, i.e., as independent and virtually any relative to one another.
And we will know for sure that in an entangled quantum state, these two electrons can be considered actually bound by an “invisible thread” with a certain length, that is, two electrons are connected and form a new “indivisible” particle. That is, the movement of two electrons in the field of cores can be described by the movement of a point located in the middle of the “invisible thread” (or in the center of a new particle, or in the center of mass, and so on), what should greatly simplify the quantum mechanical calculations.
The length of the “invisible thread” will definitely be much less than the sum of the covalent radii of hydrogen atoms, and it is this length that will determine the Coulomb repulsion between the two electrons. The length of the “invisible thread” between electrons in various chemical bonds should not greatly differ, and perhaps it will be a constant for all, without exception, chemical bonds (meaning twO-electron bonds), maybe it will be another constant.
The three-electron bond can also be seen as an entangled quantum state in which there are three electrons. Then the length of the “invisible thread” between electrons will be different from that of the twO-electron bond. You can also expect that for all, without exception, three-electron bonds the distance between electrons will be the same that is constant.
All types of chemical bonds (twO-electron, three-electron, fourelectron, five-electron, six-electron, and so on) can be seen as an entangled quantum state, in which there are electrons involved in chemical bonding. And interestingly, all entangled particles behave as they should according to the quantum theory, that is, their characteristics remain uncertain until the moment of measurement. From this point of view (the quantum mechanical point), it becomes clear the cause of failure to calculate chemical bonds “on the tip of the pen” with attempts to calculate the speed and energy of electrons and other characteristics. But these characteristics of electrons of the chemical bond (a chemical bond is a quantum entangled system, which contains electrons of the bond) cannot be determined in principle, because it is so constituted the quantum world. Logically, that what is impossible to determine is impossible to calculate in principle, what is confirmed by the history of quantum chemical calculations. That is, all attempts to calculate characteristics of electron chemical bond (speed, power, and so on) were doomed to failure from the beginning. Therefore, in our opinion, it would be more correct to consider the chemical bond as a certain new “indivisible” particle, with well-defined characteristics and spatial extension, which we called a “semi-virtual particle” [2]. In particular chemical substance the chemical bond is really indivisible. In addition, such semi-virtual particle is a fermion for the three-electron bond and other bonds with an unpaired number of electrons and total half-integral spin. And the semi-virtual particle will be a boson for the twO-electron bonds and other bonds with a paired number of electrons and total integral or zero spin. And the characteristics of a semi-virtual particle (as an integral), we can calculate. These are the characteristics of a semi-virtual particle, such as energy, spatial extension, length, and so on, that are very important for chemistry.
Calculations of a hydrogen molecule will actually come to the solution of the movement of one point in the field of two protons, which is similar to the solution of a task for the hydrogen molecular ion H2+ [22-28]. And we can expect that finally the twO-electron chemical bond will be calculated “on the tip of the pen”. Besides that, an entangled quantum state clearly demonstrates that the chemical bond is real and that it is neither an abstraction, nor a convenient concept used to describe and explain. Two electrons indeed form a chemical bond (which is a new particle), and they really “know each other’s spins”, and are in an entangled quantum state. This means that these two electrons forming a chemical bond and connected by an “invisible thread” have their own well-defined characteristics. And this bond (or this thread) is real, but not in terms of energy (if the energy of such bond really exists and is not equal to zero, then its value cannot be compared with the energies of chemical bonds).
Now, let’s try to explain the possibility of interaction of electrons and other particles, which are in an entangled quantum state, what presupposes the existence of any distance between them, for example, 1 m, or 1000 km, it is not essential, the distance can be arbitrarily long. And this distance does not affect the entangled quantum system, the particles of which miraculously know the characteristics of each other. To do this we’ll have to simulate our Universe. So, let’s imagine our infinite Universe as a finite (for convenience of description) object, such as an ordinary cube. Now let’s imagine this cube empty of matter, space-time, and in general of any fields and other characteristics, there is no matter, and, in principle, anything. Now, let’s “insert” an electron in the cube, and at once in the Universe there will appear space-time, weight, variety of fields (gravitational, electromagnetic, and so on), energy and other characteristics. After the electron appeared in the Universe, it came to life, and was born in principle. And now let’s specify that the electron is not simply located in the Universe and has specific location and spot size, and its fields (electromagnetic, gravitational, and other existing and unknown) occupy and fill the whole Universe, the entire space-time continuum, our whole infinite Universe. Now let’s step by step fill our cube (our Universe) with all elementary particles that exist in the Universe. And there is one condition that must be followed: each elementary particle occupies entirely and completely the whole Universe by its fields, energy and other characteristics, that is each particle completely fills (literally) all the infinite Universe, but at the same time it has certain coordinates (the most probable place of elementary particle detection).
With this description, our Universe, which is infinite in all senses (spatial, energy, time, etc.), will represent a giant interference of any and all elementary particles, a model of the “Interfering Universe”. And now the main thing: since each elementary particle occupies (fills) the whole Universe (and at the same time is in a particular place with certain coordinates (its most probabilistic definition in this point, or more precisely in this region of space)), then there is nothing unusual in the fact that when forming an entangled quantum state each elementary particle “knows” the characteristics of its partner in a quantum state. Elementary particles “know” everything about all the other elementary particles since they fill the same Universe (it is their common home). They (elementary particles) constantly interact, interfere, but depending on their characteristics and the characteristics of their partners (coordinates, mass, energy, field, distances between the peak densities of detection, wave characteristics, etc.) form stable bonds (most varied and not only energy) only with certain partner particles.
Conclusion
Based on the foregoing, we can conclude that our Universe, our world more precisely, is an interference pattern of each and every particle in the Universe. Now the wave-particle duality of particles, probabilistic interpretation of quantum mechanical phenomena and other quantum effects of the microcosm become intuitively clear. For example, why there is a non-zero probability of finding an electron, which rotates in a specific hydrogen atom (which is in a particular laboratory), for example, on the Moon. And it is both on the Moon and on the Sun, as well as anywhere in the space of our Universe; it really fills (takes) the whole Universe. But its presence in a particular area, “the density of presence”, so to speak (probability of detection), is different at different points of the space.
In the Interfering Universe, all elementary particles “know everything” about all the other elementary particles (since they are in the same Universe), but not all of them are suitable for all in terms of formation of various bonds (in energy and other senses). Therefore, only those particles interact, which have a well-defined set of characteristics for each other and for specific types of interactions. And our world forms as a result of such interactions.
Nothing prohibits to give a definition of the multiplicity of bond: the multiplicity of bond is the energy of bond expressed in dimensionless units.
Results and Discussion
We’ll find the dependence Multiplicity=f (L) and E=f (L) using function y=a+b/x+c/x² for С-O bonds, where the multiplicity-is multiplicity of bond, L-length of bond in Å, Е-energy of bond in kj/ mole (Table 3).
| 1/x | 1/x² | 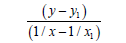 |
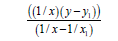 |
x (L, Å) | y (multiplicity) | |
|---|---|---|---|---|---|---|
| 0.74738416 0.82987552 |
0.55858308 0.68869338 |
10.07089756 11.00186391 |
7.52682927 9.13017751 |
1.543 1.338 1.205 |
1 2 3 |
|
| Σ | 1.57725967 | 1.24727645 | 21.07276147 | 16.65700678 | 4.086 | 6 |
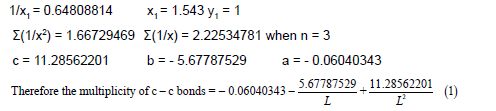
Table 3: Calculation of ratios for relation Multiplicity=f(L).
For the length of bonds let us take the findings:
H3C−OH LC-O=1.434 Ǻ (29) Multiplicity=1
H3C=O LC-O=1.206 Ǻ (29) Multiplicity=2
C≡O LC-O=1.12823 Ǻ (30) Multiplicity=3
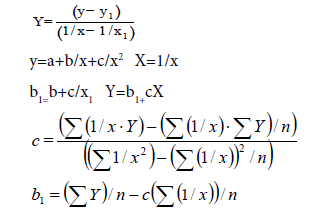
n–the number of given value Y.
Let us find a from the equality: Σy=na+bΣ(1/x)+cΣ(1/x2), when n=3
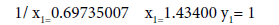
Σ(1/x2)=1.95945472 Σ(1/x)=2.41288156
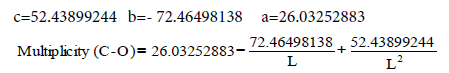
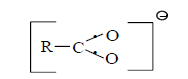
Let us calculate from the equation:
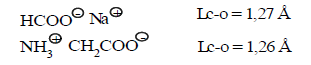 (31)
(31)
Multiplicity (L=1.27 Ǻ) =1.486
(31) Multiplicity (L=1.26 Ǻ) =1.551
(32) Multiplicity (Lс-о=1.29 Ǻ) =1.370
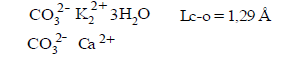
O=СO LC-O=1.162 Ǻ (33) Multiplicity (LC-O=1.162 Ǻ)=2.507
So, as we see, as expected theory of three-electrone bond, frequency of C-O bond in carboxylate anion is equal to 1.5. In carbonate anion frequency of C-O is equal to 1.37, while the carbon dioxide is equal to 2.5, which correlates well with the classical ideas (Table 4).
| 1/x | 1/x² | 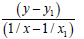 |
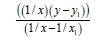 |
x (L, Å) | y (multiplicity) | |
|---|---|---|---|---|---|---|
| 0.74738416 0.82987552 |
0.55858308 0.68869338 |
2694.46159281 2554.29339132 |
2013.79790195 2119.74555296 |
1.543 1.338 1.205 |
347.9397 615.4890 812.2780 |
|
| Σ | 1.57725967 | 1.24727645 | 5248.75498413 | 4133.54345491 | 4.086 | 1775.7067 |
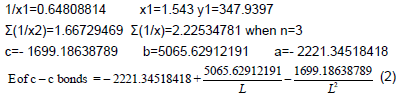
Let us calculate from the equation:
Ec–c (ethane)=347.9397 kj/mole; Ec=c (ethylene)=615.4890 kj/mole; Ec=c (acetylene)=812.2780 kj/mole.
Table 4: Calculation of ratios for relation E=f(L).
In urea С-O multiplicity of bonds equal to about 1.5, and C-N is approximately 1.7 (as shown below).
LC-O=1.27 Ǻ (34)
Multiplicity (LC-O=1.27 Ǻ) =1.486 ≈ 1.5 Multiplicity C−N=1.686
Now let’s find the dependence E=f (L) C−O bonds.
For the bonds energy let’s take the date:
C−O LC-O=1.434 Ǻ Ec-o=351.708 kj/mole (35)
C=O (for H2C=O) LC-O=1.206 Ǻ Ec-o=686.668 kj/mole (35)
C≡O LC-O=1.12823 Ǻ Ec-o=1071.773 kj/mole (30)
1/ x1=0.69735007 x1=1.43400 y1= 351.708
Σ(1/x2)=1.95945472 Σ(1/x)=2.41288156
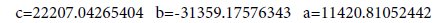
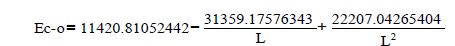
Let us find from the equation:
E (L=1.434 Ǻ)=351.708 kj/mole
E (L=1.206 Ǻ)=686.668 kj/mole
E (L=1.12823 Ǻ)=1072.542 kj/mole
O=СO LC-O=1.16213 Ǻ (36)
E (L=1.16213 Ǻ)=879.596 kj/mole=210.088 kcal/mole
O=СO LC-O=1.162 Ǻ Е (average)=192 kcal/mole D=127 kcal/mole (37)
E (L=1.162 Ǻ) =880.257 kj/mole=210.246 kcal/mole
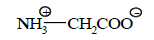
LC-O=1.26 Ǻ Е (L=1.26 Ǻ)=520.383 kj/mole
HCO−OH LC-O=1.41 Ǻ D ~ 90 kcal/mole (33)
Е (L=1.41 Ǻ) =350.243 kj/mole=83.654 kcal/mole
H3C−OH LC-O=1.434 Ǻ D ~ 90 kcal/mole (33)
E (L=1.434 Ǻ)=351.708 kj/mole=84.004 kcal/mole
CH3CO−OH LC-O=1.43 Ǻ D ~ 90 kcal/mole (33)
E (L=1.430 Ǻ)=351.038 kj/mole=83.844 kcal/mole
So we can see the binding energy calculated from the equation for C-O bond nice correlated with experimental data.
We’ll find the dependence Multiplicity=f (L) and Е=f (L) for C−N bonds.
For the bonds energy let’s take the date (35):
C−N Е=291.834 kj/mole
C=N Е=615.489 kj/mole
C≡N (for HC≡N) Е=866.709 kj/mole
For lengths of bonds let us take the date:
CH3−NH2 (LC-N=1.4714 Å) (38)
HC≡N (LC≡N=1.157 Å) (29)
C=N (LC=N=1.28 Å) (39)
We’ll find the dependence Multiplicity=f (L)
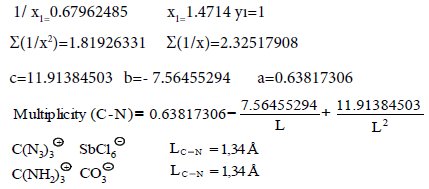
Let us find from the equation:
(32) Multiplicity (L=1.34 Å)=1.628
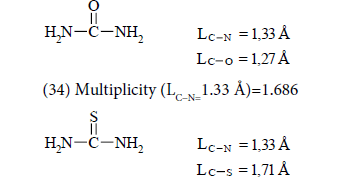
(34) Multiplicity (LC−N=1.33 Å)=1.686
We’ll find the dependence E=f (L) for C-N bonds.
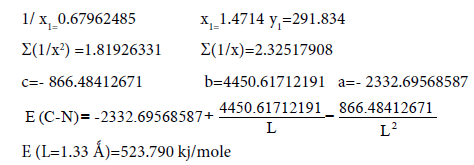
We’ll find the dependence Multiplicity=f (L) and Е=f (L) for C−S bonds. Firstly, we’ll find the dependence Multiplicity=f (L).
For lengths of bonds let us take the date:
H3C−SH Multiplicity=1 L=1.818 Å (40)
H2C=S Multiplicity=2 L=1.6108 Å (41)
C≡S Multiplicity=3 L=1.53492 Å (30)
In the molecule CS multiplicity equal to 3, what confirming the spectral data of the compounds CS, HCP, CP (30), (42), namely the frequency of fluctuations and constant anharmonicity (ωехе), what for С≡Р and С≡S bond are almost identical (Table 5):
| 1/x | 1/x² | 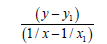 |
 |
x (L, Å) | y (Multiplicity) | |
|---|---|---|---|---|---|---|
| 0.62080954 0.65149975 |
0.38540448 0.42445193 |
14.13337066 19.71516575 |
8.77413127 12.84442560 |
1.81800 1.61080 1.53492 |
1 2 3 |
|
| Σ | 1.27230929 | 0.80985641 | 33.84853640 | 21.61855688 | 4.96372 | 6 |
Table 5: Calculation coefficients for dependence Multiplicity=f (L) for ?-S bond.
CS Lc-s=1.53492 Å D=169.6 kcal/mole ωе=1285.08 cm-1
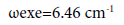
CP Lc-p=1.5583 Å D=122 kcal/mole ωе=1239.67 cm-1
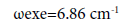
H−C≡P Lc-p=1.5421 Å νı=3216.9 cm-1
Lc-н=1.0667 Å ν2=1278.4 cm-1
ν3=674.7 cm-1
1/ x1=0.55005501 x1=1.81800 y1=1
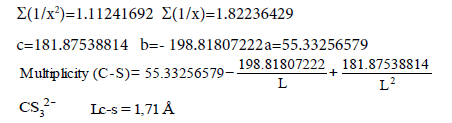
Let us find from the equation:
(32) Multiplicity (Lc-s=1.71 Å) =1.263
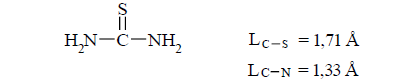 (34)
(34)
Multiplicity (C-S) =1.263 Multiplicity (C-N)=1.686
S=C=S Lc-s=1.5529 Å (42)
Multiplicity (Lc-s=1.5529 Å)=2.722
In general, we see that oxygen sulfur analogs behave quite as expected.
a) thiourea and thiocarbonates anion have slightly lowered frequency of C-S bond (compared to the C-O) (1.263 to 1.507, and 1.263 to 1.370), due to more efficient delocalization of electrons on the sulfur atom is greater (compared to an oxygen atom);
b) carbon disulfide compared with carbon dioxide multiplicity of C-S bond slightly higher than the frequency of the C-O bond (2.7 against 2.5 in carbon dioxide) that can be explained by coupling undivided pair of electrons sulfur and oxygen with a double bond and therefore more coupling in the case of sulfur atom.
We’ll find the dependence Е=f (L) for C−S bonds (Table 6). For energies of bonds let us take the date:
| 1/x | 1/x² | 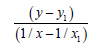 |
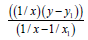 |
x (L, Å) | y (multiplicity) | |
|---|---|---|---|---|---|---|
| 0.62080954 0.65149975 |
0.38540448 0.42445193 |
6627.75936908 4436.03058434 |
4114.57621622 2890.07282747 |
1.81800 1.61080 1.53492 |
259.594 728.538 709.606 |
|
| Σ | 1.27230929 | 0.80985641 | 11063.78995342 | 7004.64904369 | 4.96372 | 1697.738 |
Table 6: Calculation coefficients for dependence ?=f (L) for ?-S bond.
C−S L=1.818 Å Е=259.594 kj/mole (35)
C=S L=1.6108 Å Е=728.538 kj/mole (35)
C≡S L=1.53492 Å Е=709.606 kj/mole (30)
1/ x1=0.55005501 x1=1.81800 y1=259.594
Σ(1/x2)=1.11241692 Σ(1/x)=1.82236429
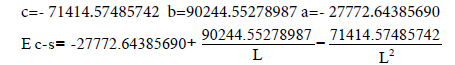
Let us find from the equation:
SC=S Lc-s=1.5529 Å Е (L=1.5529 Å) =726.729 kj/mole=173.576 kcal/mole
Еc-s (average)=128 kcal/mole (37)
We’ll find the dependence Multiplicity=f (L) and Е=f (L) for N−N bonds. For energies of bonds let us take the date:
N−N Е=160.781 kj/mole (35)
N=N Е=418.000 kj/mole (43)
N≡N Е=945.333 kj/mole (44)
For lengths of bonds let us take the date:
H2N−NH2 L=1.4530 Å (45)
HN=NH L=1.2300 Å (46)
N≡N L=1.0976 Å (47)
Firstly, we’ll find the dependence Multiplicity=f (L) (Table 7).
| 1/x | 1/x² | 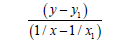 |
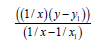 |
x (L, Å) | y (Multiplicity) | |
|---|---|---|---|---|---|---|
| 0.81300813 0.91107872 |
0.66098222 0.83006443 |
8.01430493 8.97474845 |
6.51569507 8.17670231 |
1.4530 1.2300 1.0976 |
1 2 3 |
|
| Σ | 1.72408685 | 1.49104665 | 16.98905339 | 14.69239737 | 3.7806 | 6 |
Table 7: Calculation coefficients for dependence Multiplicity=f (L) for N-N bond.
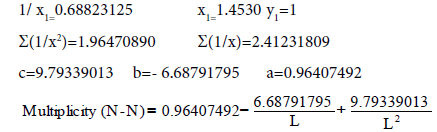
We’ll find the dependence E=f (L) for N-N bonds (Table 8).
| 1/x | 1/x² | 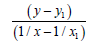 |
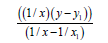 |
x (L, Å) | y (multiplicity) | |
|---|---|---|---|---|---|---|
| 0.81300813 0.91107872 |
0.66098222 0.83006443 |
2061.43150049 3520.57842393 |
1675.96056951 3207.52407428 |
1.4530 1.2300 1.0976 |
160.781 418.000 945.333 |
|
| Σ | 1.72408685 | 1.49104665 | 5582.00992443 | 4883.48464379 | 3.7806 | 1524.114 |
Table 8: Calculation coefficients for dependence ?=f (L) for N-N bond.
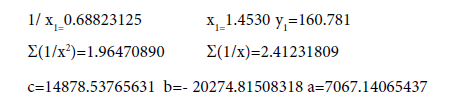
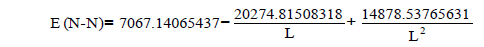
Let us find from the equation:
Multiplicity=2.835, Е=846.001 kj/mole
experimentally found Е=843.26 kj/mole (48)
As we see in the latter case are almost the same value of energy of equation identified and obtained experimentally.
We’ll find the dependence Multiplicity=f (L) for N−O bonds (Table 9).
| 1/x | 1/x² | 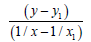 |
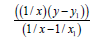 |
x (L, Å) | y (Multiplicity) | |
|---|---|---|---|---|---|---|
| 0.81699346 0.86903624 |
0.66747832 0.75522398 |
3.88312664 8.29623106 |
3.17248908 7.20972544 |
1.4530 1.2240 1.1507 |
1.0 1.5 2.5 |
|
| Σ | 1.68602970 | 1.42270230 | 12.17935770 | 10.38221452 | 3.8277 | 5.0 |
Table 9: Calculation coefficients for dependence Multiplicity=f (L) for N-? bond.
For lengths of bonds let us take the date:
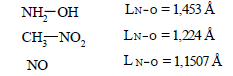 (49)
(49)
Multiplicity=1
(38) Multiplicity=1.5
(48) Multiplicity=2.5
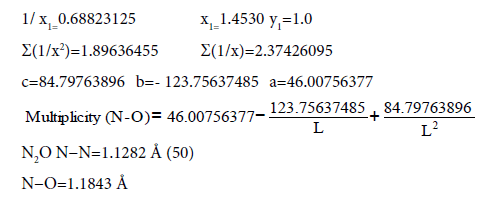
Multiplicity (N−O) (L=1.1843 Å) =1.969 ≈ 1.97
Multiplicity (N−N) (L=1.1282 Å) =2.730
NO3- L (N−O) =1.243 Å (51)
Multiplicity (L=1.243 Å)=1.328 ≈ 1.33
We’ll find the dependence Е=f (L) for N−O bond.
For energies of bonds let us take the date:
N−O E=221.900 kj/mole (52)
N=O Е=607.086 kj/mole (52)
NO L=1.15070 Å Е=626.847 kj/mole (48)
N−O L=1.453 Å (NH2−OH) (49)
Lengths L when N=O Multiplicity=2 calculated by the formula:

The value of L=1.63007893 Å is not considered as the basis of bond lengths, it is clear that this multiplicity Table 10).
| 1/x | 1/x² | 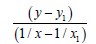 |
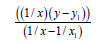 |
x (L, Å) | y (multiplicity) | |
|---|---|---|---|---|---|---|
| 0.84596462 0.86903624 |
0.71565614 0.75522398 |
2442.00695125 2239.68925320 |
2065.85148606 1946.37112471 |
1.45300000 1.18208253 1.15070000 |
221.900 607.086 626.847 |
|
| Σ | 1.71500086 | 1.47088013 | 4681.69620445 | 4012.22261077 | 3.78578253 | 1455.833 |
Table 10: Calculation coefficients for dependence ?=f (L) for N-O bond.
So, N=O Multiplicity=2 L=1.18208253 Å
N−O L=1.453 Å E=221.900 kj/mole
N=O L=1.18208253 Å Е=607.086 kj/mole
NO L=1.1507 Å Е=626.847 kj/mole
1/ x1=0.68823125 x1=1.4530 y1=221.900
Σ(1/x²) =1.94454237 Σ(1/x)=2.40323211
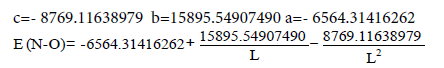
Let us find from the equation:
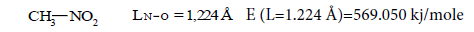
We’ll find the dependence Multiplicity=f (L) for C−P bond (Table 11).
| 1/x | 1/x² | 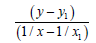 |
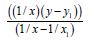 |
x (L, Å) | y (Multiplicity) | |
|---|---|---|---|---|---|---|
| 0.60975610 0.64846638 |
0.37180250 0.42050864 |
13.97761468 18.14005571 |
8.52293578 11.76321621 |
1.8580 1.6400 1.5421 |
1 2 3 |
|
| Σ | 1.25822247 | 0.79231114 | 32.11767039 | 20.28615199 | 5.0401 | 6 |
Table 11: Calculation coefficients for dependence Multiplicity=f (L) for C-P bond.
H2P−CH3 Lc−p=1.858 Å (53) Multiplicity=1
(CH3)3 P=CH2 Lc=p=1.640 Å (54) Multiplicity=2
H−C≡P Lc≡p=1.5421 Å (42), (55) Multiplicity=3
Lc≡p=1.54 Å (55)
Lc≡p=1.5421 Å (42)
1/ x1=0.53821313 x1=1.8580 y1=1
Σ(1/x²) =1.08198452 Σ(1/x)=1.79643561
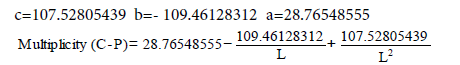
Let we see O-O bonds.
For lengths of bonds let us take the date:
O3 Lо-о=1.2717 Å (56)
O2 Lо-о=1.20735 Å (57)
H2O2 Lо-о=1.452 Å (58)
For energies of bonds let us take the date (59)
O2=2O 119.11 · 4.184=498.356 kj/mole
O3=O2+O 25.6 · 4.184=107.110 kj/mole - this dissociation energy
O−O E=33.2 · 4.187=139.008 kj/mole (60)
But energy O-O bond at 1.5 multiplicity we find the following manner:
O3=O2+O 107.110 kj/mole
O2=O+O 498.356 kj/mole
O3=O+O+O 498.356 kj/mole+107.110 kj/mole
If these three oxygen atoms forming a molecule of ozone
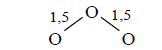
then this energy is released from the two formed three-electron bonds, so
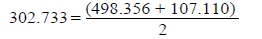
Ео-о when multiplicity 1.5=302.733 kj/mole
HO−OH Multiplicity (O-O) =1
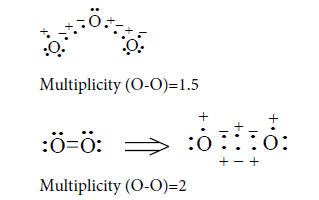
Multiplicity O-O bond in the molecule of oxygen equal to 2, despite two three-electron bond as is the interaction of unpaired electrons on the oxygen atoms with three-elecron bond that follows a compliance rules of octet (Tables 12 and 13).
| 1/x | 1/x² | 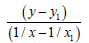 |
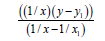 |
x (L, Å) | y (Multiplicity) | |
|---|---|---|---|---|---|---|
| 0.78634898 0.82826024 |
0.61834472 0.68601502 |
5.12065557 7.16563335 |
4.02662230 5.93500920 |
1.45200 1.27170 1.20735 |
1.0 1.5 2.0 |
|
| Σ | 1.61460922 | 1.30435975 | 12.28628893 | 9.96163149 | 3.93105 | 4.5 |
Table 12: Calculation coefficients for dependence Multiplicity=f (L) for O-O bond.
| 1/x | 1/x² | 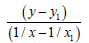 |
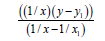 |
x (L, Å) | y (?, kj/mole) | |
|---|---|---|---|---|---|---|
| 0.78634898 0.82826024 |
0.61834472 0.68601502 |
1676.75866772 2574.95601441 |
1318.51747088 2132.73368486 |
1.45200 1.27170 1.20735 |
139.008 302.733 498.356 |
|
| Σ | 1.61460922 | 1.30435975 | 4251.71468213 | 3451.25115574 | 3.93105 | 940.097 |
Table 13: Calculation coefficients for dependence ?=f (L) for O-O bond.
H2O2 Lо-о=1.452 Å Multiplicity=1 Е=139.008 kj/mole
O3 Lо-о=1.2717 Å Multiplicity=1.5 Е=302.733 kj/mole
O2 Lо-о=1.20735 Å Multiplicity=2 Е=498.356 kj/mole

Multiplicity (L C-N=1.1679 Å)=2.897
Multiplicity (L N-O=1.1994 Å)=1.772
HNCO LH-N=0.987 Å (61) H−N=C=O
L N-C=1.207 Å
L C-O=1.171 Å
Multiplicity (L N-C=1.207 Å)=2.549
Multiplicity (L C-O=1.171 Å)=2.392
HNCS LH-N=0.988 Å (61) H−N=C=S
L N-C=1.216 Å
L C-S=1.560 Å
Multiplicity (L C-N=1.216 Å)=2.475
Multiplicity (L C-S=1.560 Å)=2.620
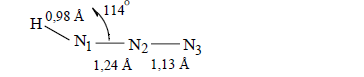
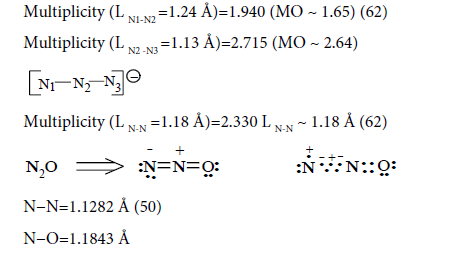
Multiplicity (L N-N=1.1282 Å)=2.730
Multiplicity (L N-O=1.1843 Å)=1.969
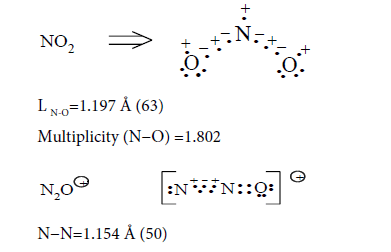
N−O=1.185 Å
Multiplicity (L N-N=1.154 Å)=2.523
Multiplicity (L N-O=1.185 Å)=1.959
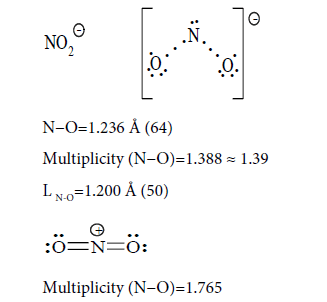
Conclusion
As exemplified in many chemical bonds (C-N, C-O, C-S, N-N, N-O, O-O) using the equation y=a+b/x+c/x² to describe the multiplicity dependence=f(L) і Е=f(L) (where multiplicity-is multiplicity of bond, L-length of bond in Å, E - energy of bond in kj /mole), gives good results and determine the multiplicity of power relations in many organic and inorganic compounds. In fact, to determine the multiplicity or energy of bond we can known length of the bonds must solve simple quadratic equation. Conversely, knowing the multiplicity or energy or bond can determine its length (again solving basic equation). This method is simple, but gives good results when analyzing the chemical bonds that are nice to coincide with the experimental data or other theoretical calculations.
Three-electron bond it is an existing particle (object)
Three-electron bond it is an existing bond, not a mathematical or physical model. And if the three-electron bond exist, then:
1) We can represent the one true formule of benzene [1]. One of the drawbacks of the resonance theory is that resonance structures do not exist in reality, and their objectification is a mistake. And assuming the existence of three-electron bond, we can represent the real formula of benzene, aromatic compounds, carboxylate anion, ozone, oxygen, etc. [19-29].
2) We can simply and clearly explain the increase in the multiplicity of benzene from 1.5 to 1.67 by MO method calculations give a value of 1.67, but Pauling from resonant structures, which is logical (2 and 4 of the electron) gave 1.5. If the multiplicity is greater than 1.5 (eg 1.67), since the communication multiplicity in classical chemistry correlates with the amount of the bonding electrons (even if it is average) like:
2 electron multiplicity 1;
4 electron multiplicity 2;
6 electrons multiplicity 3;
thene in benzene at a multiplicity of 1.67 in six (6) aromatic bonds as it further appears 1 electron:
1.67 - 0.17=1.5
6 * 0.17=1.02
At the three-electron bond in benzene and interaction through a simple explanation of the cycle - the cycle just a little compressed.
3) We can check experimentally: if the three-electron bond and interaction through the cycle are real, then it logically follows the bending real chemical bond density in benzene into benzene. It is important that the maximum density of the chemical bond will be shifted to the center of the benzene cycle link, which is what we are seeing in the atomic force microscopy images (AFM) pentacene [2].
4) Experimental predicted effects: anti-aromatic system (core system) should be flat in order to make it through the interaction cycle. Therefore, to obtain photos and AFM antiaromatic cyclobutadiene cyclooctatetraene must be on a special matrix to consolidate their atoms to make the system perfect planarity (to make it through the interaction cycle), and after that, take a picture AFM permission. And if anti-aromatic photo is received, then we should see a shift of threeelectron bonds outside the cycle, and, the picture will be in pentatsene but the loop [2].
And if think......reflect the existence of three-electron bond directly from the theory of resonance (resonance structures do not exist, in reality there is something average between them - and now think that should really be the basis of this, some real structure? .. of course the three-electron bond!!!). The theory of three-electron bond accepted for granted the existence of three-electron bonds (one axiom), everything else is derived logically.
The need to introduce three-electron bond in the description of the benzene molecule can be understood (to some extent) reading the book “Science, Philosophy, and Human Behavior in the Soviet Union” by Loren R. Graham.
Short and interesting in chapter IX “Chemistry” of this book Loren R. Graham describes the concept of resonance theory in chemistry (description of the benzene molecule), as well as its criticism of the Soviet period. Loren R. Graham-Professor at MIT (USA) on the big material of actually analyzes full of dramatic story of the interaction of dialectical materialism and Soviet scients in the period from 1917 to mid-80s. Provides a links to the original works.
Here is a quote Pauling: “We can say ... that the molecule can not be satisfactorily represented by any particular structure of the valence bond and stop trying to tie its structure and properties of the structure and properties of other molecules. But, using valence bond structures as a basis for discussion, we are using the concept of resonance can give an explanation of the properties of the molecule, directly and simply in terms of other properties of the molecules. For us, convenient, for practical reasons, talk about the resonance of molecules among several electronic structures.
Here’s another quote Academician Koptyuga:
British journalist: “If you look at the history of science after the Revolution, you will see several cases of political interference in the fundamental research ... What do you think, could this happen again? “ Academician V. Koptiug, Chairman of the Siberian Branch of the USSR: “You see, this is a very complex issue. When in the past with philosophical positions criticized the concept of resonance in chemistry ... is, from my point of view, it is true.
But when a general philosophical position of trying to solve major scientific problems, such as whether genetics science or pseudoscience, it was a mistake.
Who loves the history of chemistry (of benzene) is very interesting and informative.
Chemical bond-it is the interacting of fermions
Following from the above, interaction of two three-electron bonds in benzene (or rather interaction of three pairs) through the cycle is a typical interaction between two fermions in a molecule at a distance of 2.4 Å which is similar to the interaction of two electrons at the chemical bond formation.
Hückel rule (4n+2) for aromatic systems can be written in a different form, in the form of 2n where n - unpaired number. So, we have: 2, 6, 10, 14, 18, etc. This is also true for the electron shells in the atom and aromatic systems. The principle of the interaction of fermions always one, everywhere.
Quantum sustem of unpaired number of fermions is itself a fermion, is a classic, so three elctrons is typical fermion who will behave appropriately (just an ordinary electron is a fermion).
This is something interestin about fermions:
“Composite fermions” In addition to elementary fermions and bosons, nonrelativistic composite particles made up of more fundamental particles bound together through a potential energy are composite fermions or bosons, depending only on the number of elementary fermions they contain: A composite particle containing an even number of elementary fermions is a boson. Examples: A meson contains two fermion quarks and is a boson, the nucleus of a carbon-12 atom contains six protons and six neutrons (all fermions) and is also a boson, A composite particle containing an odd number of elementary fermions is a fermion.
Examples:
A baryon contains three quarks and is therefore a fermion, The nucleus of a carbon-13 atom contains six protons and seven neutrons and is therefore a fermion, The number of bosons within a composite particle made up of simple particles bound with a potential has no effect on whether the composite particle is a boson or a fermion.
In a quantum field theory, the situation is more interesting. There can be field configurations of bosons that are topologically twisted. These are coherent states that behave like particles, and they can be fermionic even if all the elementary particles are bosons. This situation was discovered by Tony Skyrme in the early 1960s, so fermions made of bosons are named Skyrmions.
Fermionic or bosonic behavior of a composite particle (or system) is seen only at large distances (compared to the size of the system). At proximity, where spatial structure begins to be important, a composite particle (or system) behaves according to its constituent makeup. For example, two atoms of helium cannot share the same space if it is comparable by size to the size of the inner structure of the helium atom itself (~10-10m)-despite bosonic properties of the helium atoms. Thus, liquid helium has finite density comparable to the density of ordinary liquid matter.
Chemical bond-is a new indivisible particle
Chemical bond - is a new indivisible particle, electrons, in which the are entangled in quantum state.
The existence of large aromatic monocycles has been proved impossible based on interaction of three-electron bonds through the cycle at distances between the bonds (through the cycle) greater than 3.5 Å due to the lack of energy interaction (the length of chemical bonds is in the range of distances 0.74 Å-3.5 Å).
The chemical bond (twO-electron and three-electron) is considered on the assumption that the electrons in a chemical bond can be regarded as being in an entangled quantum state, that is, the chemical bond is seen as a new “indivisible” particle.
There has been provided an algorithm for calculating the twoelectron chemical bond “on the tip of the pen” [3].
Alternative description of the chemical bond
Description of the chemical bond using the π- and σ-bond this is one of the alternative description. The correct and fair description of the chemical bond there is description of multiple bonds with the help of bent bonds.
At symposium Pauling categorically stated: “There may be chemists who believe that it is extremely important innovation was the introduction of σ, π-description for the double or triple bond and conjugated systems instead of describing via bent bonds. I would argue that σ, π-description is less satisfactory than the description by means of curved links that this innovation is only transitory and will soon wither away.
Pauling was right, the theory of valence bonds, which used σ, π-description chemical bonding, lost its leading position.
“Two different explanations for the nature of double and triple covalent bonds in organic molecules were proposed in the 1930s. Linus Pauling proposed that the double bond results from two equivalent tetrahedral orbitals from each atom, [7] which later came to be called banana bonds or tau bonds. Erich Hückel proposed a representation of the double bond as a combination of a σ-bond plus a π-bond [9-11]. The Hückel representation is the better-known one, and it is the one found in most textbooks since the late-20-th century. There is still some debate as to which of the two representations is better [12], although both models are mathematically equivalent. In a 1996 review, Kenneth B. Wiberg concluded that “although a conclusive statement cannot be made on the basis of the currently available information, it seems likely that we can continue to consider the σ/π and bent-bond descriptions of ethylene to be equivalent [2]. Ian Fleming goes further in a 2010 textbook, noting that “the overall distribution of electrons [...] is exactly the same” in the two models [13]. Double bond is 2 equivalent σ-bond (π-bond is not present) (Figures 55 and 56).
Becouse of this, description bonds with σ- and π-bonds is first method of description, description bonds with bent bonds is second method of description, description bonds with three-electron bonds is third method of description. The correctness of the theory verified compliance of the experimental facts and predictions of new effects.
Theory of three-electron bond predict in aromatic interesting effect: anti-aromatic system (core system) should be flat in order to make it through the interaction cycle. Therefore, to obtain photos and AFM antiaromatic cyclobutadiene cyclooctatetraene must be on a special matrix to consolidate their atoms to make the system perfect planarity (to make it through the interaction cycle), and after that, take a picture AFM permission. And if anti-aromatic photo is received, then we should see a shift of three-electron bonds outside the cycle, and, the picture will be in pentatsene but the loop [2].
As well as the curvature of bonds into pentacene is observed on the photo AFM (Photo 1).
But other than that, if you use the three-electron bond in benzene at once solved a lot of problems:
Drawn real structure of the benzene molecule (and this is already an achievement) [1].
2. Are explained easily and clearly aromaticity of benzene and antiaromaticity cyclobutadiene. It becomes obvious why at 4n+2 aromatic and at 4n antiaromatic [1].
3. Simply calculated delocalization energy of benzene (58,416 kcal/ mol) [1].
4. Easily and clearly explains the increase in the multiplicity of benzene from 1.5 to 1.66 (due to the interaction between the threeelectron bonds through a series of benzene slightly compressed) [1].
5. Easy and simple to explain the difference of external and internal signals of protons in [18]-annulene [1].
6. You can picture structure of furan, thiophene, pyrrole, naphthalene, anthracene, graphite, oxygen, ozone, carboxylate anion and other organic and non-organic compounds [1].
And still need to clearly understand that the existence of twoelectron chemical bond does not follow from fundamental interactions. But must follow!!!
Therefore, the chemical bond and does not appear “on the tip of the pen”, and introduced explanation exchange interaction and the like, since it is clear and proven that a purely Coulomb interaction (electromagnetic) is not sufficient to describe chemical bond (where there is more than one electron). By the way one-electron bond is displayed “on the tip of the pen.”
Think ... with chemical bonding distance between the electrons (couple) should be the maximum that was the least the Coulomb repulsion between them and at the same time the electrons need to be concentrated in the middle of chemical bond to make it existed! With the chemical bond and the twO-electron three-electron all hard. Therefore, when a breakthrough in theoretical terms in this direction chemistry waiting for great things (you will agree that this chemistry is still an empirical science, and quantum mechanical calculations are not very used experimenters, such as synthetic organic chemistry, etc.).
Urea molecule
Look at the picture which shows the urea molecule with the calculations.
Classic structure Real structure

LC-N=1.33 Å, LC-O=1.27 Å (8)
Multiplicity C−N=1 Multiplicity C−N (L=1.33 Å)=1.686
Multiplicity C−O=2 Multiplicity C−O (L=1.27 Å)=1.486
EC-N=291.834 kj/mole ЕC-N (L=1.33 Å)=523.790 kj/mole
EC-O=728.538 kj/mole (for R2C=O) EC-O (L=1.27 Å)=496.940 kj/mole
E1=EC-O+2EC-N=1312.206 kj/mole E2=EC-O+2ЕC-N=1544.520 kj/mole
ΔE=E2 - E1=1544.520 kj/mole - 1312.206 kj/mole=232.314 kj/mole
So, the energy gain for a real urea molecule (with three-electron bonds) as compared to the classic structure makes 232.314 kj/mole (55.487 kcal/ mole). Calculations for other molecules may be done in the same way. This example illustrates why the three-electron bonds appear at all: it proves to be that the three-electron bonds are “more poor” by energy and formation of three-electron bonds is energetically more advantageous. The multiplicity of C-N bonds in the molecule of urea-1.686. Think, this mean the C-athom connected with two atoms of nitrogen (urea) bonds with a multiplicity of approximately 1.7, fold that is one of the C-N bond is almost 2. Are classical structure transmits real formula of urea molecules?
The multiplicity of C-O bond (urea) of approximately 1.5. That is the classic formula of urea (to which all accustomed to in the school and at university) almost not reflects the real structure of the urea. Naturally, the explanation of the conjugation of the unshared pair of electrons of nitrogen with C-N bond are right. But classical formule (without arrows) does not show the structure of the molecule.
And note that the corresponding resonance structure (in which a multiplicity of the C-N bond - 2) can be written, but of course you can not write a resonance structure in which the two C-N bond have multiplicity 2.
Oxygen
Without regard of three-electron bond its impossible to portray oxygen molecule that has a multiplicity of connection 2 and two unpaired electrones. This experimental fact that multiplicity ob bond in the oxygen molecule is equal to two, and at the same time there are 2 unpaired electrones (oxygen molecule has paramagnetic properties, it is an experimental fact, the multiplicity of bond correlates with the energy of bond, with IR spectra and the like, and there is no doubt that the multiplicity of oxygen molecule is two).
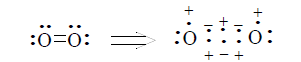
“Generally, the octet rule defines the state of the three-electron bond, that is, the distribution of the electrons, the energy of their interaction with each other and other unpaired electrons, the fact and the extent of belonging of the three-electron bond electrons to one or another atom.” [28-32]. This fact is yet another confirmation of the existence of three electrone bond.
Model of the interfering universe
Model of the Interfering Universe, a perfect union of the microcosm and macrocosm (Photos 2-4).
These three photos illustrate to some extent, the model of the Interfereing Unuverse also demonstrate the unity of the microcosm of macrocosm.
“... In the Interfering Universe, all elementary particles “know everything” about all the other elementary particles (since they are in the same Universe), but not all of them are suitable for all in terms of formation of various bonds (in energy and other senses). Therefore, only those particles interact, which have a well-defined set of characteristics for each other and for specific types of interactions. And our world forms as a result of such interactions.” [3].
I express my deep gratitude to my son, Bezverkhniy Vitaliy Volodymyrovich, for participation in the development of the theory (some parts as a co-author), and for his invaluable contribution to the English translation.