Thermodynamic properties of water and hydrocarbon mixtures at high temperatures and pressures are of particular interest for the oil and chemical industries, organic chemistry, geology and mineralogy, new separation processes, and biology. Hydrocarbons together with other impurities must be removed from water. And water content in a hydrocarbon parallel with a quality loss in a product can have an effect on the equipment causing corrosion. Hence, data on the solubility and the volatility under different thermo baric conditions are important for refining technology. The investigation of thermal properties of water-hydrocarbon systems allows to find the degree of hydrocarbon extraction by water at critical and supercritical parameters. It is important in the fields of biology (biological degradation without char formation), for the chemical and petrochemical industries, for the separation technologies.

In addition, gas and oil pools are in direct interaction with water, and their accumulation and migration depend significantly on solubility in water. When increasing the depth of gas and oil occurrence, the thermo baric conditions change and their solubility in water gains the importance for gas and oil recovery. In this connection, it is essential to know phase equilibrium between water, gas, and oil. In view of the complexity of a phase behavior in multicomponent mixtures the regularities of a phase behavior are appropriate to be studied on the basis of binary systems consisting of water and oil components. The analysis and classification of a binary system behavior allow revealing behavior regularities of complex systems.

This paper is generalizing our previous work on the water-npentane and the water-n-hexane systems investigation.

The main features in vapor-liquid and liquid-liquid behavior of mixtures were started to study as far back as the beginning of 20th century. However, the theoretical interpretation and prediction of phase equilibrium in a wide range of temperatures and pressures were begun more lately.

Krichevskii and his followers were those who made a substantial contribution to understanding of phase equilibrium at high temperatures and pressures [1,2]. They considered theoretical aspects of critical phenomena, the solubility of gas in liquids and of liquid in gases.

The phase equilibrium of a mixture is described using different approaches: the cubic equation of state, lattice and group models, etc.

Peng-Robinson equation, Redlich-Kwong-Soave equation and their numerous modifications are most often used. But for many systems involving long chains, high-boiling components and highpolar substance, cubic equations of state predict often incorrect phase behavior. For the description of such asymmetric systems the Huron and Vidal approach was applied [3]. This approach integrates a state equation with a model of Gibbs excess energy of liquid mixtures in order to deduce the law of mixing. A resulting expression is flexible well enough and can be useful for good presentation of experimental data but this empiric in origin. Christoforakos and Franck [4] developed an equation for the description and prediction of phase equilibrium and critical curves of liquid binary systems at high pressures using the basic concept of Van der Vaals equation. Computer modeling based on Karnakhan-Starling expression with the temperature dependence of particle diameter describes a repulsing. An expression for the attraction was obtained as a squared known potential. Equation parameter values are deduced from critical data of pure components or are determined from the correlation of a selected molecular interaction model. The equation with two fitting parameters was used for systems H₂O-N, H₂O-CH, H₂O-Xe to describe the critical curves. The theoretical investigation of phase equilibrium in binary systems employing the van der Vaals equation was performed by Scott and van Konynenburg [5]. This work presents the classification of phase diagrams that was developed by Rowlimson and Swinton [6]. The experimental examination of phase diagram topology provided the separation of 6 general types of phase behavior. Scott and van Konynenburg showed the applicability of the single-fluid van der Vaals equation of the state for qualitative description of experimental phase diagrams. Boshkov and Mazur [7] applied the state equation to the study of phase behavior of binary Lennard-Jones systems, gave the qualitative description of phase diagrams for the most of real mixtures and revealed new types of diagrams. Boshkov specified a region of the state equation parameter describing the phase diagrams. Ermakova and Anikeev [8,9] used the Redlich-Kwong-Soave cubic equation at appropriate selection of binary interaction coefficients as a model for the estimation of phase states of complex mixtures under near-critical and supercritical conditions and also for the description of gas-gas equilibrium.

The analysis of works indicates that cubic equations of states are more suitable for the description of mixtures with a non-polar component such as hydrocarbons. However, the equation parameters are applicable for only a concrete system and concrete thermo baric conditions.

State equations based on partial molecular models are presented in works [10-13]. They are more universal than cubic equations of states but not quite satisfactory for practical use: often required parameters lack and fail to be directly checked for many classes of mixtures.

Currently, methods employing the Skiold-Jorgensen group equation [14] and UNIFAC model [15] gain sufficiently extensive acceptance for modeling of phase equilibria in associated mixtures. The first equation is usually applied for the description of systems with light components, and when using the latter one meets difficulties with simultaneous simulation of phase equilibria liquid-vapor and liquid-liquid.

The most applicable model among existing ones suited for the prediction of a phase behavior is a hole group quasi-chemical model [16,17]. It eliminates restrictions of lattice models. Lattice models consider stiff lattices, all sites of which are occupied by component molecules providing description of a liquid state only but not a vapor phase. The evaluation of liquid-vapor equilibrium has to exploit any state equation of a vapor phase. Lattice models don`t consider both the dependence of liquid properties on a pressure and a change in a volume at solution formation. Hole models describe more completely the thermodynamics of solutions and simultaneously vapor and liquid phases with allowance for volume effects at the solution formation. According to this model the structure of a liquid is a quasi-lattice, sites of which can be occupied by molecules or be empty (holes). These models provide, within the framework of the quasi-chemical approximation, the description of a wide range of thermodynamic properties of liquids and solutions formed both by polar and by nonpolar components, and liquid-vapor equilibrium in single-, two-, and milticomponent systems.

Apart from works describing a general picture of binary system behavior there are researches touching some detailed aspects of a phase behavior. Blagonravov [18] proposed a model computation for boundary coexistence curves of two immiscible liquids based on information for pure components properties. The approach is based on the generality of regularities of complex system behavior on the one hand and on the other hand, on bounded self-oscillating systems. Baburina and Maklashina [19] performed the calculating and graphic study of NRTL model [20]. Model parameters were defined to be directly dependent on a type of binary system. Also for the description of a solution behavior the Wilson model gained widespread acceptance [21].

Available theoretical models predict right the common regularities in the phase behavior of such complex systems, but they are far from a quantitative interpretation even for binary systems water - hydrocarbon. Various equations of state can quantitatively describe thermodynamic properties of mixtures only using experimental data. Additionally, coefficients of equations are individual for each substance and for different regions of ranges parameters. The only procedure for right and precise determination of the phase behavior of multicomponent systems is an experiment. Oil and gas from different depositions distinct in composition and, consequently, differs in a phase behavior. In connection with this, it is rational to study binary systems of hydrocarbons and water; and basing on obtained data to calculate the properties of oil and gas mixtures at state parameters corresponded to reservoir conditions.

Experimental Investigations

There are very few experimental measurements on phase equilibrium and thermal properties of water and hydrocarbon systems at high temperatures and pressures. Available measurements are unsystematic and fragmentary. Probably, this is stemmed from the complexity and labor intensity of thermobaric conditions for realization of such measurements. Alwani and Schneider [22] measured, using a constant volume piezometer, the molar volume of water-benzol system at 613.15 K and pressures up to 200 MPa involving liquid and gas state and evaluated molar volume values. Namiot et al. [23,24], using a constant volume piezometer, measured PVTx properties for methane water solutions for 1- 4 temperature values and pressures from 2 to 60 MPa and for hexane, octane, and bensol water solutions at 2-15 MPa. The authors showed that redundant molar volumes can be both positive and negative. De Loos et al. [25,26] performed visual measurements of the phase equilibrium and critical phenomena n-pentane, n-hexane, and propane water mixtures in temperature intervals from 600 to 675 K and pressures from 15 to 170 MPa. They reported the lines of phase equilibrium and critical parameters of transitions gas-gas and liquid-gas. The critical curve of these systems began in a critical point of pure water and crossed a temperature minimum at an increase in pressure. In a constant volume and variable volume combining piezometer, Yiling et al. [27] investigated two phase equilibrium for systems water - n-butane and water - n-hexane in ranges of temperature from 500 to 700 K, pressure from 10 to 300 K, and concentrations 0.10 - 0.95 mass fraction of water. Molar volumes for homogeneous phase were determined. A critical curve behaved similarly to that obtained by De Loos et al. Brunner [28] with the aid of cylindrical optical cell of high pressure obtained three-phase lines and lines of critical points for 23 mixtures of n-alkane - water. He obtained, all the critical lines had a break and for these mixtures gas-gas equilibrium of a second order was characteristic. The author reported P and T parameters of critical and three-phase line but did not indicate concentrations they belonged. Extensive researches on the isochoric heat capacity and PVTx properties of n-hexane - water and n-heptane - water have been performed on the Amirkhanov hightemperature adiabatic calorimetry by Stepanov et al. [29,30], Mirskaya et al. [31,32], Rasulov et al. [33-35]. These measurements are most systematic for these mixtures and involve a wide range of temperatures, pressures, densities, and concentrations. These works are the only performed on the examination of the isochoric heat capacity. The value of these measurements along with determination of phase diagrams and critical lines is that the azeotropy lines of studied mixtures were evaluated. Roof [36] defined using a visual apparatus the parameters of the upper critical end point (UCEP) for 16 binary water-hydrocarbon systems and established their dependence on a molecular weight in a homologous series. The solubility limits of binary hydrocarbonwater systems and P-T data in a region involving the parameters of pure water critical point were reported by Rebert and Hayworth [37]. These systems were shown to be characterized by two unique states: the critical point of vapor formation and critical solution point. The first one determined the limit of the mutual solubility of two liquid phases; the second one specified the point of the complete miscibility under a minimal pressure. The mutual miscibility of water and hydrocarbon solutions at different temperatures and pressures were investigated by many authors [38-42]. The heat of water solution in hydrocarbons was shown to be much higher than the heat of hydrocarbon solution in water. This fact is related with that the water was found to be soluble in hydrocarbons better than hydrocarbons in water.

Analyzing experimental works on the estimation of volume properties and phase equilibrium of water-hydrocarbon systems we can conclude that:

1. PVTx properties are measured for gaseous mixtures with high water content in a wide interval of temperatures and pressures. For low and medium concentrations of water such measurement are few or practically absent.

2. The researches on volume properties of a liquid phase are performed for individual values of state parameters. Systematic measurements of volume properties in a wide interval of state parameters lack.

3. Presented lines of critical points of these systems are not always associated with concentration.

4. Т - Ð, Т - ρ, and Ð - ρ phase diagrams of liquid-liquid, liquidvapor transitions and their change with a concentration are absent for many mixtures.

In this regard, in order to reveal the common regularities of volume behavior, and of phase equilibria for liquid-liquid, liquid-vapor, and gas-gas solutions it is necessary to perform the evaluation of their thermal properties in a wide range of parameters, including critical and supercritical states and in the whole interval of concentrations from 0 to 1.

Experimental Apparatus

The high-temperature and high-pressure constant-volume pvT apparatus was used in this work for measurements of the pvTx behavior of water+hydrocarbone mixture in the vicinity of critical point and at supercritical conditions, including one- (pvT), two-(L-G), and threephases (L-L-G). Both the method and apparatus are similar to those used in our previous publications [43-54] for measuring the pvTx properties for binary mixtures of H₂O+n-C₅H₁₂, H₂O+n-C₆H₁₄, and n-butanol in the critical and supercritical regions. The detailed description of the physical and theoretical parts, as well as uncertainty assessment have been given in our previous publications [43-54]. Only a brief review will be given here. The apparatus consistes of: 1) piezometer; 2) system for the temperature control; 3) system for the filling piezometer with the sample; and 4) system for the pressure measurements. The main part of the apparatus is a piezometric tube. The cylindrical piezometric tube is made of stainless steel 12Ð¥18Ð?10Т with 8.721 mm inside diameter, 394 mm full length, 2.7 mm wall thickness.

The thermostat is a massive, solid copper block mounted on the piezometric tube to maintain the homogeneity of the temperature distribution along the length of the piezometric tube. A three-section heating element is mounted on the surface of solid cooper block to control the temperature in the thermostat. The temperature difference between various sections of the cooper block was less than 0.02 K. The temperature homogeneity along the piezometer was controlled with three HPTR-3, differential thermocouples, and regulating heaters. Temperature of the piezometer was measured with platinum resistance thermometer (PRT-10) which was calibrated against a standard thermometer of the VNIIFTRI (Russian NIST, Moscow). All temperatures have been recorded on ITS-90. The uncertainty in temperature control and temperature measurements has been within 20 mK and 15 mK, respectively.

Pressure has been measured with a diaphragm-type zero indicator made in laboratory and mounted on one of the sides of the piezometric tube. The stop valve has been mounted on the other side. Basic part of the diaphragm-type zero indicator is membrane which was made of stainless steel (0.08 mm thick and 32 mm in diameter). The membrane is clamped between two flanges by a cutting edge seal, whose inside surface is conic. At the neutral position the membrane has been touched the surface of the cylinder. The distance between the membrane and electrical-contact was about 0.2 mm. Membrane had been separating the measured liquid and the liquid (castor oil) that transmitted pressure to the manometer. The sensitivity of the zero indicator was within 0.005 MPa. At low pressures (up to 1 MPa) the pressure in the piezometer was measured with zero indicator and standard manometer. At high pressures the pressure was measured with dead-weight pressure gauge MP-600(Russia). The maximum uncertainty of pressure measurements is within 0.0005 MPa at low pressures (below 1 MPa) and 0.001 MPa at high pressures.

The inner volume V_TP of the piezometer at given T and P was calculated by taking into consideration the corrections for the elastic pressure deformation and thermal expansion. The internal volume of the piezometer 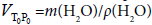at ambient temperature T₀=293.15 K and pressure P₀=0.1 MPa was calculated on the base of the well established values of density ρ(H₂O) and mass of the water m(H₂O) in the piezometer (IAPWS formulation, Wagner and Pruss [53]). The uncertainty in density of pure water at this condition is less than δρ<0.001% [20]. The derived value of piezometer’s volume at these conditions was 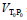=(21.160 ± 0.020) cm³. The densities of the sample at given temperature T and pressure P were calculated using the simple relation ρ(T,P)=m/VPT, where the variations of the piezometer volume VPT with temperature T and pressure P were calculated using the thermal expansion coefficient of the piezometer material, α=(changed from 16 × 10^-6 K^-1 to 17.5 × 10^-6 K^-1 in the temperature range from 273 to 673 K), and the pressure expansion coefficient of the piezometer, β=4 × 10^-5 MPa^-1

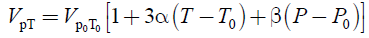(2)

The uncertainties in α and have been found both about 5% and their effect on the density determination is negligibly small [43-52]. All masses were determined with an uncertainty of 5 × 10^-4 g. The volume of the piezometer VTP at given temperature T and pressure P was measured with an uncertainty of 0.011%. Taking into account the uncertainties of temperature and pressure, the combined expanded (k=2) uncertainty of density measuring has been estimated as 0.15% at low densities and 0.12% at high densities. In order to avoid the additional uncertainty in the density measurements, which were introduced by a dead volume, the diaphragm-type zero indicator has been mounted on one of the sides of the piezometer in the unloaded state. To check the reproducibility of the experimental density values some of the measurements were repeated at a few (5-6) times at selected temperatures and pressures. The reproducibility of the data excels 99.9%. To test the apparatus and procedures of the measurements and confirm the accuracy of the measurements, initially the density of triple-distilled water was measured and compared with values calculated from IAPWS formulation [53]. The agreement between test measurements for pure water and IAPWS [53] formulation is good, the absolute average deviation is AAD=0.13% (St. dev=0.06%). The good agreement between the present data and IAPWS [53] calculations for pure water in the critical and supercritical conditions confirms the reliability and high accuracy of the measurements for water+npentane and water+n-hexane mixture and provides an assurance that our instrument was functioning correctly. The sample mixtures have been vigorously mixed using a stirrer (cylindrical form with conic end) made from stainless steel.

Mixture components were weighed on the analytical balance with an uncertainty not more than 0.5 mg. The mixture was prepared using water with conductivity of 5.56 mkSm.m^-1, n-pentane with in purity 99.91% and n-hexane with in purity 99.94%.

The work presents the investigation results for phase equilibria of binary immiscible systems under standard conditions (n.hexanewater, n.pentane-water) basing on measurements of PVTx-properties in temperature intervals from 300 K to 680 K, pressures up 60 MPa, and a wide range of densities with a constant-volume piezometer. The measurements have covered a wide range of state parameters involving the regions of liquid-liquid (L-L) and liquid-gas (L-G), critical and supercritical regions. Thermal properties of n.hexane-water system have been obtained for 11 water concentrations (in mole fraction): 0.166, 0.201, 0.234, 0.257, 0.347, 0.615, 0.827, 0.918, 0.935, 0.964, 0.977, and for 15 water concentrations of n.pentane-water system: 0.110, 0.143, 0.174, 0.203, 0.209, 0.214, 0.572, 0.800, 0.862, 0.881, 0.903, 0.925, 0.942, 0.973, and 0.987. The PVT-properties have been measured in a wide range of state parameters. For each concentration measurements have been made along ten-eleven isochores covering a wide interval of vapor and liquid isochores (Figure 1). Figure 1 presents a PT-diagram. The diagram depicts breaks along the isochores corresponded to the phase transitions L-L and L-G (Figure 2). The join of break points yields the lines of phase equilibrium separating the three-phase region from two-phase one and two-phase region from single phase one. A break-free isochore passes through a temperature maximum point - the cricondentherm of phase equilibrium line. We note that cricondentherm point not always corresponds to the critical temperature. Two bends or breaks are observed for the majority of measured isochores. Break points on PT-diagram correspond to phase transitions occurring in these binary systems. Depending on a piezometer filling and a mixture concentration two different phase transitions along isochores are observed. 1: a) the solution of water in hydrocarbon (liquid-liquid transition); b) a transition of obtained mixture into vapor. 2: a) the transition of hydrocarbon vapor into liquid; b) the solution of water in hydrocarbon. 3: a) the transition of hydrocarbon into vapor; b) the transition of water into vapor. 4: a) the simultaneous solution of water and hydrocarbon and the transition of the mixture into vapor in upper critical end point (UCEP). 5: a) the solution of hydrocarbon in water (liquid-liquid transition); b) the transition of obtained mixture into vapor. 6: “gas-gas” transition. For this reason, the phase diagram of hydrocarbon-water system has a rather complex appearance. The critical diagram of hydrocarbonwater system can be divided into three parts in the dependence of concentration. The first part involves a range from pure hydrocarbon to a concentration corresponded to UCEP. In this region the lines of phase transitions L-L (solution of water in hydrocarbon, i.e., the three-phase line) and L-V, and their critical parameters approach one to another at increase of water content. At concentrations 0.257 for n.hexane-water and 0.209 for n.pentane-water, the lines of phase equilibria L-L and L-V have a common point and coincident critical parameters (Figure 3) This point is UCEP and is the azeotrope point, because in this point all three phases co-exist: hydrocarbon liquid, water liquid, and vapor. Critical parameters of this point are: Т_к=463.8 K and Ð_к=4.57 MPa for n.hexane-water system and Т_к=495.3 K and Ðк=5.28 MPa, and they are in accordance with reference data [25-29,39]. On addition of water to a system, a common pressure rises, the water content in gas phase increases, and a part of water dissolves in hydrocarbon. The pressure in a system is increasing before the start of the formation of second liquid phase and a system transits from two-phase into three-phase state. The equilibrium range between hydrocarbon liquid and gas phase is bounded by the three-phase equilibrium curve, the line of critical points lower locus, and the vapor curve of pure hydrocarbon. The temperature of the three-phase equilibrium is lower than the boiling temperature of pure components at pressures equal to the pressure of the three-phase equilibrium. The region of three-phase equilibrium on PT-diagram is a curve moving from UCEP towards lower temperature and pressure. Hydrocarbon and water liquids are in equilibrium at temperatures lower than the UCEP temperature. When rising the temperature, the solubility of water in liquid hydrocarbon increases, and the lower pressure boundary of equilibrium between liquid phases is on the rise. The solubility of water in liquid hydrocarbon at UCEP is maximal and the UCEP temperature is the highest, at which all three phases exist, over that a hydrocarbon-rich liquid phase disappears.

Figure 1: The experimental pressure dependence on temperature for the mixture 0.987 Н₂О+0.013 n/С₅Н₁₂ (mole fractions) along isochors: 1-96.94 kg/ m³; 2-193.9 kg/m³; 3-290.8 kg/m³; 4-387.8 kg/m³; 5-484.69 kg/m³; 6-581.6 kg/ m³; 7-613.6 kg/m³; 8-644.8 kg/m³; 9-678.56 kg/m³; 10-707.6 kg/m³.

Figure 2: The P-T diagram, schematically. I-the isohore ρ=ρ_c without kinks and bends, i.e., the cricondetherm on the phase equilibrium line; II and III-the isochors at ρ>ρ_c and ρ<ρ_c, accordingly. The kink points at II and III are according to the liquid-liquid phase transitions (with transition points Т1 and Т2), and the bend points are according to the liquid-vapour phase transitions (with transition points Т₃ and Т₄).

Figure 3: The lower locus of critical points for water-n/pentane system.

The change of states in a mixture can be explained by microscopic phenomena in mixtures occurring as the dependence from a change of external fields (temperature, pressure).

The second part is between concentration of UCEP and 0.882 m.f. of water. In this region, in the initially the hydrocarbon liquid turns into vapor, the phase equilibrium lines of which are shown in Figure 4, and then the water liquid transits into vapor. The critical pressure and temperature for the transition of hydrocarbon liquid into vapor are the same as for UCEP close to highest water concentrations in a mixture but the critical densities differ. P(T) dependence of transits water liquid into vapor in Figure 5 is smooth and monotonous without any pecularities. On phase diagrams for these concentrations the critical conditions of transition liquid-vapor are not implemented. For the concentrations over 0.882 mole fraction of water the first transition corresponds to the solution of hydrocarbon in water (liquid-liquid transition), these phase equilibrium lines are represented in Figure 4. The critical parameters for this transition decrease with increasing of water concentration, similary to the range of lower concentrations of water, where the parameters of the three-phase line decrease with increasing of hydrocarbon concentration. The second transition in the region of concentrations over 0.882 mole fractions of water corresponds to the transition of water liquid into vapor. And on isopleths in Figure 5, a local S-form temperature maximum and minimum appear. The difference between extremes increases. In the range of high pressure all isopleths depict a steep ascent. In upper region of critical points a temperature minimum, corresponded to concentrations 0.935 mole fractions and 0.925 mole fractions for mixtures with pentane and hexane mixtures respectively, is found. A point pertained to the temperature minimum divides the two-phase region into two parts. A right part relates to L-G equilibrium and with a rise in the temperature is aligned with the critical point of water. A left part of the two phase region corresponds to the “gas-gas” equilibrium of the second order and continues over the critical temperature of water (Figure 6). The point, where “gas-gas” and L-V curves are aligned, is named a double critical point (DCP). On P(T) diagram the region of the phase equilibrium “gas-gas” is limited by a curve moving from DCP towards higher T and P and by an isotherm moving towards higher pressures. Curve 1 (Figure 7) conforms to the composition of liquid phase (L1) being in the three-phase equilibrium (L1-L2-G). The composition of a second liquid phase (L2), being in the three-phase equilibrium, is shown by line 5 drawn through experimental points in the region of high content of water. Horizontal line 3 corresponds to the three-phase line, nonvariant equilibrium of UCEP (L1-G-L2) and phase (L1-G). This line is the line of the phase transition of hydrocarbon liquid into vapor in the presence of water liquid.

Figure 4: The phase equilibrium lines: the hydrocarbon liquid-gas line (1-5) and the liquid-liquid lines for n/pentane-water system at the concentrations: 1-0, 214; 2-0, 572; 3-0, 80; 4-0, 862; 5-0, 881; 6-0, 903; 7-0, 925; 8-0, 942; 9-0, 973; 10-0.987 (mole fractions of water).

Figure 5: The phase equilibrium aqueous liquid-gas line for n/pentanewater system at the different concentrations of water.

Figure 6: The P-T critical diagram for n/hexane-water and for n/ pentane-water. 1 and 2-the upper regions of critical line for pentane and for hexane, accordingly.

Figure 7: The T-x critical diagram for n/pentane-water system. 1, 3 and 5-the three-phase coexistence lines; 2 and 4-the lower and the upper regions of critical line, accordingly.

When increasing of carbon atoms number in hydrocarbon, the critical curve is displaced to lower pressures and higher values of water concentration. Parameters Т_Ñ?=625.5 K, ÐÑ?=33.7 MPa and Т_Ñ?=627.7 K, Ð_Ñ?=30.9 MPa, correspondingly, obtained for DCP of n-pentane+water and n-hexane+water systems are in good accordance with literature data [25-28].

All above said suggests that the phase behavior of water mixtures with pentane and hexane belongs to III type of Scott and Van Konynenburg classification. III-type phase diagram is divided into 3 temperature regions: the lower branch of critical points (L1-G), the absence of critical points of phase transition L-G, and the upper branch of critical points (Figures 6 and 7).

New measurements of the PVTx properties of H₂O+n-C₅H₁₂ and H₂O+n-C₆H₁₄ mixtures were obtained along liquid and vapor isochors from 63 to 713 kgm-3 as a function of temperature in rang 303÷684K at pressures up to 66MPa. These regions include upper and lower branches of the critical curves, three-phase line, liquid-gas, liquidliquid, and gas-gas phase equilibrium curves. The measured data were used to determine the values of three-phase and two-phase phase boundary properties and critical parameters of mixtures. The values of the upper critical point parameters (TUCEP=463.85K, PUCEP=4.575MPa, and the concentration x=0.257 mol fraction of H2O for H₂O+n-C₅H₁₂ mixtures, and TUCEP=495.3K, PUCEP=5.28MPa and the concentration x=0.257 mole fraction of H2O for H₂O+n-C₆H₁₄ mixtures) are derived from three-phase curve data. The phase equilibrium of these systems, the liquid-gas phase -equilibrium curves at low water concentration and first phase transition characteristic at all concentration along isohores are investigated only in our papers.

We are acknowledged for Bashirov Rustam Radifovich and Atayev Hamid Muhtarovich for the assistance in our work and the discussions.