Journal of Thermodynamics & Catalysis

Journal of Thermodynamics & Catalysis
Open Access

ISSN: 2157-7544

+44 1300 500008

Research Article - (2016) Volume 0, Issue 0

View PDF Download PDF

Thermodynamic Description of the Gd-Sb and Gd-Bi-Sb Systems

Mbamalu ON1*, Antunes E2, Silosini N3, Samsodien H4 and Syce J1,3
1Discipline of Pharmacology, School of Pharmacy, University of the Western Cape, Bellville 7535, South Africa
2Department of Chemistry, University of the Western Cape, Bellville 7535, South Africa
3South African Herbal Science and Medicine Institute, University of the Western Cape, Bellville 7535, South Africa
4Discipline of Pharmaceutics, School of Pharmacy, University of the Western Cape, Bellville 7535, South Africa
*Corresponding Author: Mbamalu ON, Discipline of Pharmacology, School of Pharmacy, University of the Western Cape, Bellville 7535, South Africa, Tel: +27219593229/2190, Fax: +278615107002 Email:

Abstract

The thermodynamic modeling and optimization of the Gd-Sb and Gd-Bi-Sb systems were critically carried out by means of the CALPHAD (CALculation of PHAse Diagram) technique. The solution phases, liquid, bcc, rhomb and hcp(Gd) were described by the substitutional solution model. The compounds, β-Gd5(Bi, Sb)3, γ-Gd4(Bi, Sb)4, δ-Gd(Bi, Sb), δ′-Gd(Bi, Sb), ε-Gd16Sb39 and GdBi2 were treated as the formulae (Gd)m/m+n(Gd, Bi, Sb)n/m+n using two sublattice model in the Gd-Bi-Sb system. A self-consistent thermodynamic description of the Gd-Sb and Gd-Bi-Sb system were developed. The isothermal section at 300 K for the Gd-Bi-Sb system in the literature were reproduced in the present work.

Keywords: Gd-Bi-Sb system; Phase diagram; CALPHAD technique; Thermodynamic properties

Introduction

In past years, the advanced magnetic materials and its potential as an energy savings technology greatly stimulated the interest of researchers and promoted the rapid development of magnetic refrigeration. Magnetic refrigeration could be realized by utilizing the heat release or absorption caused by the magnetic entropy change DSM of a magnetic material due to a magnetic field change DH [1]. The recent discovery of the giant magnetocaloric effect in Gd5(Si2Ge2) [1], gave further impulse towards the development of new materials [2]. Gd4Sb3 was one of the candidates for magnetic refrigerant near room temperature (266 K). Substitution of Bi for Sb in Gd4Sb3 increased its Curie temperature Tc up to 330 K [3]. The calculation of phase diagrams (CALPHAD) method, which was a powerful approach to save cost and short time during development of materials, effectively provided a clear guideline for material design. So in order to better understand the interactions of Gd and Sb with Bi and design high performance thermoelectric materials, it was important to study the thermochemical properties and the phase equilibria concerning the Gd-Bi-Sb system and to obtain the thermodynamic parameters of the system.

Binary Systems

To obtain a thermodynamic description of a ternary system, the thermodynamic description of each involved binary system was necessary.

Gd-Bi system

The partial phase diagram of the composition range 0–60 at % Bi of the Gd-Bi binary system was firstly measured by Gambino [4], and three intermetallics, Gd5Bi3, Gd4Bi3 and GdBi, were reported in this system. In 1993, the phase diagram of the Gd-Bi system was re-determined and a new phase, GdBi2 was discovered [5]. The four intermetallics, Gd5Bi3, Gd4Bi3, GdBi2 and GdBi, were reported in the Gd-Bi binary system. All of the information of the Gd-Bi binary system was accompiled by Wang et al. [6]. The Gd-Bi binary system was assessed by Wang et al. [6]. Figure 1 presented the calculated phase diagram of Gd-Bi system using the thermodynamic description of Wang et al. [6]. The thermodynamic parameters obtained by Wang et al. [6] were adopted in the present work.

Calculated-Gd-Bi-diagram

Figure 1: Calculated Gd-Bi phase diagram by Wang et al. [6].

Bi-Sb system

The Bi-Sb system was very simple and only two phases, liquid and rhomb(Bi, Sb) in this system, which was calculated by Dinsdale et al. [7]. The calculated the thermodynamic parameters [7] were accepted in the assessment of the Bi-Sb-Sn system [8] and the Ag-Bi-Sb system [9]. So the thermodynamic parameters obtained by Dinsdale et al. [7] were adopted in the present work. Figure 2 presented the calculated phase diagram of Bi-Sb system using the thermodynamic description of Dinsdale et al. [7]. Figure 2a presented the Bi-Sb system reproduced using the Thermo-Calc software [10] and Figure 2b presented the Bi-Sb system reproduced using the Pandat software [11].

Thermo-Calc-software

Figure 2a: Calculated Bi-Sb phase diagram by Dinsdale et al. [7], reproduced using the Thermo-Calc software [10].

Calculated-Bi-Sb-Dinsdale

Figure 2b: Calculated Bi-Sb phase diagram by Dinsdale et al. [7], reproduced using the Pandat software [11].

Gd-Sb system

The Gd-Sb system was firstly determined in the concentrationl range 0-60 at% Sb by Gambino [4]. Later, Gerasimov [12] updated all the invariant equilibria temperatures. The whole composition and temperature ranges in the Gd-Sb phase diagram were established by Abdusalyamova et al. [13]. The four intermediate compounds, Gd5Sb3, Gd4Sb3, GdSb2, and GdSb were reported in this system. Recently, the previously called “GdSb2’’ phase was determined to be Gd16Sb39 [14], which was confirmed in the Gd-Bi-Sb ternary system [15]. So the Gd-Sb phase diagram was revised by Borzone et al. [14]. All of the information of the Gd-Sb system was compiled by Li et al. [16]. The updated phase diagram was assessed by Li et al. [16]. The thermodynamic parameters of the Gd-Sb system were well reproduced [16], but the parameters of Bcc(Gd) were difficult to reproduce the temperature of the Bcc(Gd). In the present work, to assess the Gd-Bi-Sb ternary system, the model of the five intermediate compounds, Gd5Sb3, Gd4Sb3, Gd16Sb39, α-GdSb (GdSb-low temperature as GdSb-LT) and β-GdSb(GdSbhigh temperature as GdSb-HT), was re-built to cosistent with other thermodynamic parameters of the relative compounds in the Gd-Bi system [6]. So the thermodynamic parameters of the five intermediate compounds were re-assessed in the present work. Figure 3 presented the calculated phase diagram of Gd-Sb system using the thermodynamic parameters of the five intermediate compounds calculated in this work and the thermodynamic parameters of the liquid assessed by Li et al. [16].

Calculated-Gd-Sb-parameters

Figure 3: Calculated Gd-Sb phase diagram in the present work and using the parameters of liquid by Li et al. [16], and comparison with the experimental data [13].

Experimental Information on the Gd-Bi-Sb System

The information about the Gd-Bi-Sb system was very scarce. Recently, the phase diagram of the Gd-Bi-Sb ternary system had been determined at room temperature using X-ray powder diffraction and differential scanning calorimetry analysis by Jian et al. [15]. There were composed of six single-phase regions, six two-phase regions and one three-phase region. No ternary compound was reported in the Gd-Bi- Sb ternary system. The compounds, Gd5Sb3, Gd4Sb3 and GdSb (α-GdSb and β-GdSb) in the Gd-Sb system and their relative compounds, Gd5Bi3, Gd4Bi3 and GdBi in the Gd-Bi system were formed the continuous solid solutions, respectively. So the six single-phase regions are (Gd, Bi, Sb) solid solution (α phase), Gd5(Bi, Sb)3 solid solution (β phase), Gd4(Bi, Sb)3 solid solution (γ phase), Gd(Bi, Sb) solid solution (δ and δ′ phases), Gd16Ga39 (ε phase) phase and Gd (Hcp phase) phase in the Gd-Bi-Sb system. The maximum solid solubility of Gd in (Gd, Bi, Sb) at room temperature was determined to be 7.5 at %. The solid solubility of Gd in the other phases could not be detected. The above information was described in detail in the Ref. [15].

Thermodynamic Models

Unary phases

The Gibbs energy function for the element i (i=Gd, Bi, Sb) in the phase φ (φ = liquid, hcp, rhomb) was described as follows,

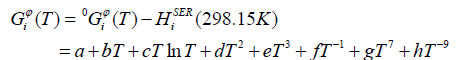thermodynamics-catalysis(1)

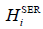Where thermodynamics-catalysis (298.15 K) was the molar enthalpy of the element i at 298.15 K in its standard element reference (SER) state, hcp for Gd, rhomb for Bi and Sb. The Gibbs energy of the element i(i=Gd, Bi, Sb), 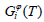thermodynamics-catalysis, in its SER state, was denoted by GHSERi, i.e.,

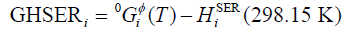thermodynamics-catalysis(2)

In the present work, the Gibbs energy functions were taken from the SGTE(Scientific Group of Thermodata Europe) pure elements database compiled by Dinsdale [17] and listed in Table 1.

Solution phases

In the Gd-Bi-Sb system, there are three solution phases, liquid, hcp, and rhomb. Their molar Gibbs energies are described by the following expression:

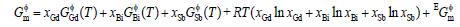thermodynamics-catalysis (3)

where R is the gas constant; xGd, xBi and xSb were the mole fractions of the pure elements Gd, Bi and Sb, respectively; 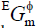thermodynamics-catalysiswas the excess Gibbs energy, expressed by the Redlich-Kister polynomial [18].

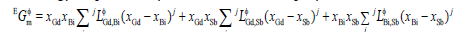
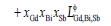thermodynamics-catalysis

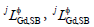thermodynamics-catalysis(4)

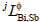where thermodynamics-catalysisand thermodynamics-catalysis were the binary interaction parameters between elements Gd and Bi, Gd and Sb, and Bi and Sb, respectively. Its general form was

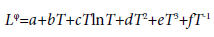thermodynamics-catalysis(5)

but in most case only the first one or two terms were used according to the temperature dependence of the experimental data. 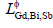thermodynamics-catalysis was the ternary interaction parameter expressed as:

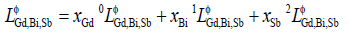thermodynamics-catalysis(6)

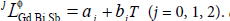where thermodynamics-catalysis aj and bj were the parameters to be optimized in this work.

Intermetallic compounds

The compounds, Gd5Sb3, Gd4Sb3 and GdSb (GdSb-high temperature named as GdSb-HT and GdSb-low temperature named as GdSb-LT) in the Gd-Sb system and their relative compounds, Gd5Bi3, Gd4Bi3 and GdBi in the Gd-Bi system were formed the continuous solid solutions, respectively. So the three continuous solid solutions single-phase (named as Gdm(Bi, Sb)n), β-Gd5(Bi, Sb)3, γ-Gd4(Bi, Sb)3 δ-Gd(Bi, Sb) and δ′-Gd(Bi, Sb) in the Gd-Bi-Sb system were treated as two-sublattice model (Gd)m/m+n(Gd, Bi, Sb)n/m+n. In the Gd-Bi-Sb system, δ-Gd(Bi, Sb) and δ′-Gd(Bi, Sb) were the relative compounds, GdSb-high temperature (as GdSb-HT) and GdSb-low temperature (as GdSb-LT) in the Gd-Sb system. The Gibbs energy per mole of formula unit Gdm(Bi, Sb)n was given by the following expression:

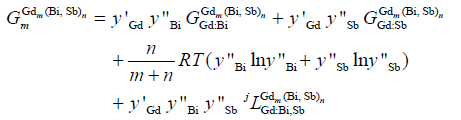thermodynamics-catalysis(7)

The parameter 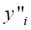thermodynamics-catalysis was the site fractions of Bi or Sb (i = Bi or Sb) on the second sublattices; the parameter 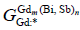thermodynamics-catalysis represented the Gibbs energies of the compound Gdm(Bi, Sb)n when the second sublattice was occupied by only one element Bi or Sb, respectively, which were relative to the enthalpies of pure rhomb for Bi and Sb in their SER state. 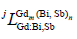thermodynamics-catalysis represented the jth interaction parameters (j=0) between the elements Bi or Sb on the second sublattice. The other binary intermetallic compounds, GdBi2 and Gd16Sb39 in the Gd- Bi and Gd-Sb system were treated as stoichiometric compounds, and were used as the two-sublattice model, which was consistented with the relative binary system [6,16].

Assessment procedure

A general rule for selection of the adjustable parameters was that only those coefficients determined by the experimental values should be adjusted [19]. The assessment was carried out by means of the optimization module PARROT of the thermodynamic software Thermo-Calc [10], which could deal with various kinds of experimental information. A careful examination of thermodynamic descriptions of the Gd-Bi [6] and the Bi-Sb [7] systems were made. The thermodynamic optimization of the Gd-Sb and Gd-Bi-Sb system were carefully performed in this work. The thermodynamic parameters for the Gd-Sb system were optimized on the basis of the experimental information available in the experimental data. The thermodynamic parameters of liquid were taken from the assessed data [16]. The compounds, Gd5Sb3, Gd4Sb3, Gd16Sb39, α-GdSb and β-GdSb in the Gd-Sb system were assessed in the present work. The experimental results of Jian et al. [15] were given more weight during the process of optimization. The thermodynamic parameters for the Gd-Bi-Sb system were optimized on the basis of the experimental information available in the experimental data [15]. The experimental results of Jian et al. [15] were given more weight during the process of optimization. The thermodynamic parameters of liquid, bcc, rhomb and hcp in the Gd-Bi- Sb system, are obtained by a combination of the corresponding Gibbs energy functions from the assessments of the binary systems using Muggianu interpolation of binary excess terms [20]. The interaction parameters of the Gd-Bi and Bi-Sb system and the liquid of the Gd- Sb system were taken from the calculated data assessed by Wang et al. [6], Dinsdale et al. [7] and Li et al. [16]. The binary parameters of the compounds of the Gd-Sb system and the ternary parameters in the Gd- Bi-Sb system were optimized according to the experimental data [15].

Results and Calculations

The Gd-Bi and the Bi-Sb systems were assessed by Wang et al. [6], and Dinsdale et al. [7], respectively. Their thermodynamic descriptions were accepted in the present work and listed in Table 1. Figures 1 and 2 presented the Gd-Bi and Bi-Sb phase diagrams using the thermodynamic description of Wang et al. [6], and Dinsdale et al. [7], respectively. There was some different at low temperature using the Thermo-Calc Software [10] and the Pandat software [11] to reproduce the Bi-Sb phase diagram, as shown in Figures 2a and 2b.

Figure 3 presented the Gd-Sb phase diagram using the thermodynamic description of liquid assessed by Li et al. [16] and the calculated result of the compounds in the present work, and comparison with the experimental data [13]. Figure 4 presented the calculated standard enthalpies of formation in The Gd-Sb system at 300 K and comparison with the experimental data [14]. The reference states are hcp for Gd and rhomb for Sb. Reasonable agreement was obtained between the calculated results and the experimental data [14]. Figure 5 was the calculated enthalpies of mixing of liquid in the Gd-Sb system at 6000 K.

Calculated-enthalpies-experimental

Figure 4: Calculated enthalpies of formation at 300 K in the Gd-Sb system and comparison with the experimental data [14] and the calculated data [16]. The reference states for the elements were hcp for Gd and rhomb for Sb.

Calculated-enthalpies-mixing

Figure 5: Calculated enthalpies of mixing of liquid at 6000 K in the Gd-Sb system. The reference states were liquid for Gd and Sb.

The calculated standard enthalpies of formation in the Gd-Sb system and comparison with the experimental data [14,21-25] were shown in Figure 4 and Table 2. The calculated invariant equilibria in the Gd–Sb system were listed in Table 3. As shown in the tables, a very good agreement was obtained between the calculated results and the experimental data [14]. The Gd-Bi-Sb system were optimized on the basis of the available experimental data [15]. The thermodynamic description of the Gd-Bi-Sb system obtained in the present work was shown in Table 1. Figure 6 were the calculated isothermal section at 300 K using the present thermodynamic description in comparison with experimental data [15] in the Gd-Bi-Sb system. Satisfactory agreements were obtained between the calculated results and the experimental data [15] in Figure 6. For the Bi-Sb phase diagram at low temperature (under 300 K), the rhomb was broken down into two component parts rhomb1 and rhomb2, as shown in Figure 2b. So there was some different at the rhomb phase side from the experiment data [15].

enhancing-cerebellum-pontine

Figure 6: Calculated isothermal section of the Gd-Bi-Sb system at 300 K by the present thermodynamic description and comparison with the experimental data [15].

Compound Temperature, K ΔfH References
Gd5Sb3 300 -110 [16]
Gd5Sb3 673 -141.9 [23]
Gd5Sb3 300 -103.664 This work
Gd5Sb3 673 -93.623 This work
Gd4Sb3 300 -116 [16]
Gd4Sb3 673 -145.1 [23]
Gd4Sb3 300 -118.254 This work
Gd4Sb3 673 -108.228 This work
GdSb 300 -120 [16]
GdSb 300 -131 [25]
GdSb 693 -102.5 [21]
GdSb-LT 300 -118.994 This work
GdSb-LT 753 -106.672 This work
GdSb-LT 693 -108.429 This work
Gd0.52Sb0.48 ˜753 -137.1 [22]
Gd16Sb39a 300 -78 [16]
Gd16Sb39 300 -87.697 This work
Gd16Sb39 803 -73.972 This work
GdSb2 803 -96 [24]

aThe nominal composition of GdSb2 was determined by Borzone et al. [14] to be Gd16Sb39 (70.91 at %Sb).

Table 2: Calculated formation enthalpy (kJ mole of atoms).

Reaction T (K) x(Sb) Reference
Liq. + bcc(Gd) →hcp(Gd) 1505 0.065 0.025 0.02 [13]
  1501 0.058 0.0191 0.0183 [16]
  1505 0.0821 0.0408 0.0387 This work
Liq. + hcp(Gd) →Gd5Sb3 1393 0.135 0.025 0.375 [13]
  1390 0.1018 0.0402 0.375 [16]
  1393 0.1329 0.0685 0.375 This work
Liq. + Gd5Sb3 →Gd4Sb3 1913 0.35 0.375 0.4286 [13]
  1917 0.3029 0.375 0.4286 [16]
  1913 0.3016 0.375 0.4286 This work
Liq. + Gd4Sb3 →βGdSb 2043 0.389 0.4286 0.50 [13]
  2048 0.3517 0.4286 0.50 [16]
  2043 0.3515 0.4286 0.50 This work
Liq. → GdSb-HT 2403 0.50 0.50 - [13]
  2401 0.50 0.50 - [16]
  2403 0.50 0.50 - This work
GdSb-HT →GdSb-LT 2113 0.50 0.50 - [13]
  2113 0.50 0.50 - [16]
  2114 0.50 0.50 - This work
Liq. + GdSb-LT →Gd16Sb39 1053 0.958 0.7091a 0.50 [13]
  1054 0.9665 0.709 0.50 [16]
  1053 0.9514 0.709 0.50 This work
Liq. + Gd16Sb39 →rhomb 897 >0.99 0.7091a 1.0 [13]
  903 >0.99 0.709 1.0 [16]
  903 0.9984 0.709 1.0 This work

aThe nominal composition of GdSb2 was determined by Borzone et al. [14] to be Gd16Sb39 (70.91 at %Sb).

Table 3: Invariant reactions of the Gd–Sb system.

Conclusion

The thermodynamic parameters in the Gd-Sb and Gd-Bi-Sb ternary system were critically evaluated from the experimental information available in the literature. A set of self-consistent thermodynamic parameters describing the Gibbs energy of each individual phase as a function of composition and temperature was derived.

Acknowledgements

This work was supported by National Natural Science Foundation of China (NSFC) (Grant No. 51264012), Jiangxi Province Science and Technology Support Program (Grant No. 20141BBE50006) and Jiangxi Province Natural Science Foundation (Grant No. 20142BAB206015), and the China Postdoctoral Science Foundation (Grant No. 2014M551712).

References

  1. Palfai TP, Monti PM, Ostafin B, Hutchison K (2000) Effects of nicotine deprivation on alcohol-related information processing and drinking behavior. J Abnorm Psychol 109: 96-105.
  2. Harrison EL, Hinson RE, McKee SA (2009) Experimenting and daily smokers: episodic patterns of alcohol and cigarette use. Addict Behav 34: 484-486.
  3. Howell A, Leyro T, Hogan J, Buckner J, Zvolensky M (2010) Anxiety sensitivity, distress tolerance, and discomfort intolerance in relation to coping and conformity motives for alcohol use and alcohol use problems among young adult drinkers. Addictive Behaviors 35:1144-1147.
  4. Krukowski RA, Solomon LJ, Naud S (2005) Triggers of heavier and lighter cigarette smoking in college students. J Behav Med 28: 335-345.
  5. Reed MB, Wang R, Shillington AM, Clapp JD, Lange JE (2007) The relationship between alcohol use and cigarette smoking in a sample of undergraduate college students. Addictive Behaviors 32: 449-464.
  6. Hughes JR, Kalman D (2006) Do smokers with alcohol problems has more difficulty quitting? Drug Alcohol Depend 82: 91-102.
  7. Hurt RD, Offord KP, Croghan IT, Gomez-Dahl L, Kottke TE, et al. (1996) Mortality following inpatient addictions treatment: Role of tobacco use in a community-based cohort. JAMA: Journal of the American Medical Association 275: 1097-1103.
  8. Lisha NE, Carmody TP2, Humfleet GL2, Delucchi KL2 (2014) Reciprocal effects of alcohol and nicotine in smoking cessation treatment studies.  Addict Behav 39: 637-643.
  9. Taylor B, Rehm J (2006) When risk factors combine: The interaction between alcohol and smoking for aerodigestive cancer, coronary heart disease, and traffic and fire injury. Addictive Behaviors 31: 1522-1535.
  10. Jarvis CM, Hayman LL, Braun LT, Schwertz DW, Ferrans CE, et al. (2007) Cardiovascular risk factors and metabolic syndrome in alcohol- and nicotine-dependent men and women. J CardiovascNurs 22: 429-435.
  11. Joseph AM, Willenbring ML, Nugent SM, Nelson DB (2004) A randomized trial of concurrent versus delayed smoking intervention for patients in alcohol dependence treatment. Journal of Studies on Alcohol, 65: 681-691.
  12. Kodl M, Fu SS, Joseph AM (2006) Tobacco cessation treatment for alcohol-dependent smokers: when is the best time? Alcohol Res Health 29: 203-207.
  13. Fu S, Kodl M, Willenbring M, Nelson D, Nugent S, et al. (2008) Ethnic differences in alcohol treatment outcomes and the effect of concurrent smoking cessation treatment. Drug and Alcohol Dependence 92: 61-68.
  14. Holt LJ, Litt MD, Cooney NL (2012) Prospective analysis of early lapse to drinking and smoking among individuals in concurrent alcohol and tobacco treatment. Psychology of Addictive Behaviors 26:561-572.
  15. Centers for Disease Control and Prevention (CDC) (2009) Cigarette smoking among adults and trends in smoking cessation - United States, 2008. MMWR Morb Mortal Wkly Rep 58: 1227-1232.
  16. Irving LM, Seidner AL, Burling TA, Thomas RG, Brenner GF (1994) Drug and alcohol abuse inpatients' attitudes about smoking cessation. J Subst Abuse 6: 267-278.
  17. Macnee CL, Talsma A (1995) Development and testing of the barriers to cessation scale. Nurs Res 44: 214-219.
  18. Orleans CT, Rimer BK, Cristinzio S, Keintz MK, Fleisher L (1991) A national survey of older smokers: treatment needs of a growing population. Health Psychol 10: 343-351.
  19. Kristeller JL (1994) Treatment of hard-core, high-risk smokers using FDA approved pharmaceutical agents: An oral health team perspective. Health Values 18: 25-32.
  20. Asher MK, Martin RA, Rohsenow DJ, MacKinnon S, Traficante R, et al. (2003) Perceived barriers to quitting smoking among alcohol dependent patients in treatment. Journal of Substance Abuse Treatment 24: 169-174.
  21. Martin RA, Rohsenow DJ, MacKinnon SV, Abrams DB, Monti PM (2006) Correlates of motivation to quit smoking among alcohol dependent patients in residential treatment. Drug Alcohol Depend 83: 73-78.
  22. Marlatt GA, Gordon JR (1985) Relapse prevention. New York: Guilford Press.
  23. Velicer WF, DiClemente CC, Prochaska JO, Brandenburg N (1985) Decisional balance measure for assessing and predicting smoking status. J PersSoc Psychol 48: 1279-1289.
  24. DiClemente CC, Prochaska JO (1982) Self-change and therapy change of smoking behavior: a comparison of processes of change in cessation and maintenance. Addict Behav 7: 133-142.
  25. Curry SJ, Grothaus L, McBride C (1997) Reasons for quitting: intrinsic and extrinsic motivation for smoking cessation in a population-based sample of smokers. Addict Behav 22: 727-739.
  26. Baha M, Le Faou AL (2010) Smokers' reasons for quitting in an anti-smoking social context. Public Health 124: 225-231.
  27. Curry SJ, McBride C, Grothaus LC, Louie D, Wagner EH (1995) A randomized trial of self-help materials, personalized feedback, and telephone counseling with nonvolunteer smokers. J Consult Clin Psychol 63: 1005-1014.
  28. Saunders JB, Aasland OG, Babor TF, de la Fuente JR, Grant M (1993) Development of the Alcohol Use Disorders Identification Test (AUDIT): WHO Collaborative Project on Early Detection of Persons with Harmful Alcohol Consumption--II. Addiction 88: 791-804.
  29. First MB, Williams JB, Spitzer RL, Gibbon M (2002) Structured Clinical Interview for DSM-IV-TR Axis I Disorders, Clinical Trials Version (SCID-CT). New York: Biometrics Research, New York State Psychiatric Institute.
  30. Brown RA, Lejuez CW, Kahler CW, Strong DR (2002) Distress tolerance and duration of past smoking cessation attempts. J Abnorm Psychol 111: 180-185.
  31. Heatherton TF, Kozlowski LT, Frecker RC, Fagerström KO (1991) The Fagerström Test for Nicotine Dependence: a revision of the Fagerström Tolerance Questionnaire. Br J Addict 86: 1119-1127.
  32. Pomerleau CS, Carton SM, Lutzke ML, Flessland KA, Pomerleau OF (1994) Reliability of the Fagerstrom Tolerance Questionnaire and the Fagerstrom Test for Nicotine Dependence. Addict Behav 19: 33-39.
  33. Fagerstrom KO, Heatherton TF, Kozlowski LT (1990) Nicotine addiction and its assessment. Ear Nose Throat J 69: 763-765.
  34. Filbey FM, Claus E, Audette AR, Niculescu M, Banich MT, et al. (2007) Exposure to the taste of alcohol elicits activation of the mesocorticolimbicneurocircuitry. Neuropsychopharmacology 33: 1391-1401.
  35. Fleming MF, Barry KL, MacDonald R (1991) The alcohol use disorders identification test (AUDIT) in a college sample. Int J Addict 26: 1173-1185.
  36. Cherpitel CJ (1995) Analysis of cut points for screening instruments for alcohol problems in the emergency room. J Stud Alcohol 56: 695-700.
  37. Macnee CL, Talsma A (1995) Predictors of progress in smoking cessation. Public Health Nurs 12: 242-248.
  38. Curry S, Wagner EH, Grothaus LC (1990) Intrinsic and extrinsic motivation for smoking cessation. J Consult Clin Psychol 58: 310-316.
  39. McBride CM, Pollak KI, Bepler G, Lyna P, Lipkus IM, et al. (2001) Reasons for quitting smoking among low-income African American smokers. Health Psychol 20: 334-340.
  40. Bonn-Miller MO, Zvolensky MJ (2009) An evaluation of the nature of marijuana use and its motives among young adult active users. Am J Addict 18: 409-416.
  41. Buckner JD, Zvolensky MJ, Schmidt NB (2012) Cannabis-related impairment and social anxiety: the roles of gender and cannabis use motives. Addict Behav 37: 1294-1297.
  42. Agrawal A, Budney AJ, Lynskey MT (2012) The co-occurring use and misuse of cannabis and tobacco: a review. Addiction 107: 1221-1233.
  43. Degenhardt L, Hall W, Lynskey M (2001) The relationship between cannabis use and other substance use in the general population. Drug Alcohol Depend 64: 319-327.
  44. Cohen J, Cohen P (1983) Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum.
  45. Cohen J, Cohen P, West SG, Aiken LS (2003) Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah, NJ US: Lawrence Erlbaum Associates Publishers.
  46. Lipkus IM, Feaganes JR, Green JD, Sedikides C (2001) The Relationship Between Attitudinal Ambivalence and Desire to Quit Smoking Among College Smokers. Journal of Applied Social Psychology, 31: 113-133.
  47. Wilson SJ, Creswell KG, Sayette MA, Fiez JA (2013) Ambivalence about smoking and cue-elicited neural activity in quitting-motivated smokers faced with an opportunity to smoke.  Addict Behav 38: 1541-1549.
  48. Festinger LA (1957) A theory of cognitive dissonance. Evanston, IL: Row, Peterson.
  49. Markowitz LJ (2000) Smoker's perceived self-exemption from health risks. Psi Chi Journal of Undergraduate Research 5: 119-124.
  50. Jamieson P, Romer D (2001)What do young people think they know about the risks of smoking? In P. Slovic (Ed.), Smoking: Risk, perception, and policy (pp. 51-63). Thousand Oaks, CA US: Sage Publications, Inc.
  51. Schane RE, Glantz SA, Ling PM (2009) Social smoking implications for public health, clinical practice, and intervention research. American Journal of Preventive Medicine 37: 124-131.
  52. DaniJA, De Biasi M (2001) Cellular mechanisms of nicotine addiction. PharmacolBiochemBehav 70: 439-446.
  53. Nestler EJ (2005) Is there a common molecular pathway for addiction? Nat Neurosci 8: 1445-1449.
  54. Ehrman RN, Robbins SJ, Bromwell MA, Lankford ME, Monterosso JR, et al. (2002) Comparing attentional bias to smoking cues in current smokers, former smokers, and non-smokers using a dot-probe task. Drug Alcohol Depend 67: 185-191.
  55. Kerst WF, Waters AJ (2014)Attentional retraining administered in the field reduces smokers’ attentional bias and craving.
  56. Wiers RW, Rinck M, Kordts R, Houben K, Strack F (2010) Retraining automatic action-tendencies to approach alcohol in hazardous drinkers. Addiction 105: 279-287.
  57. Raupach T, West R, Brown J (2013) The most "successful" method for failing to quit smoking is unassisted cessation. Nicotine Tob Res 15: 748-749.
  58. Korte KJ, Capron DW, Zvolensky M, Schmidt NB (2013) The Fagerström test for nicotine dependence: do revisions in the item scoring enhance the psychometric properties? Addict Behav 38: 1757-1763.
Citation: Mbamalu ON, Antunes E, Silosini N, Samsodien H, Syce J (2016) HPLC Determination of Selected Flavonoid Glycosides and their Corresponding Aglycones in Sutherlandia frutescens Materials. Med Aromat Plants 5: 246.

Copyright: © 2016 Mbamalu ON, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Top