Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2016) Volume 0, Issue 0
N-Acetylglycine is an important organic chemical and pharmaceutical intermediate. The solubility of N-Acetylglycine in methanol+Acetonitrile was measured in the temperature ranging from 278.15 K to 333.15 K. In the processing of the experimental data, we use three kinds of equations. There are the Combined Nearly Ideal Binary Solvent/Redlich–Kister (CNIBS/R–K) equations and the simplified Jouyban–Acree equation. All equations can be well applied. The CNIBS/R–K equations are relatively better. We used the van’t Hoff equation to determine the thermodynamic properties of N-Acetylglycine further more, including the entropy, enthalpy, and Gibbs energy.
Keywords: N-Acetylglycine; Solubility-temperature dependence; Pharmaceutical intermediate; Correlation; Enthalpy; Jouyban–Acree equation; CNIBS/R–K equation
N-Acetylglycine (Figure 1, CAS: 543-24-8, MW=117.10) is a long needle crystal and its crystal structure has been reported in the literature [1,2]. N-Acetylglycine is important organic chemical intermediate for many chemical products, such as glycine, aspartame and other amino acids. It is also important pharmaceutical intermediate for Acetyl glutamine that can be used for the patient to promote department of neurosurgery coma after surgery. N-Acetylglycine was widely used in pharmaceutical [3], pesticide [4], chemical industry [5] and other fields. N-Acetylglycine is prepared from paraformaldehyde; acetamide, carbon monoxide with a catalyst system, then gained with concentrating and filtrating, and can be purified by crystallization (Figure 2). Therefore, to know the relationship between N- Acetylglycine solubility with temperature and solvent composition is very important for the preparation and purification of products. As far as we know, it has not been reported about the solubility data of N-Acetylglycine in (methanol+Acetonitrile) mixtures. So we provided the helpful and valuable information on the crystallization of N-Acetylglycine. We chose methanol and acetonitrile as the binary solvent mixtures system in this paper. The reason to make such a choice is that the solubility of N-Acetylglycine in methanol is better than acetonitrile in previous study. In this paper, the solubility of N-Acetylglycine in methanol+Acetonitrile mixtures was determined between 278.15 K and 333.15 K at standard atmospheric pressure (101.325 kPa) by the dynamic method. The experimental data measured was correlated with two forms of Redlich–Kister (CNIBS/R–K) equation and the simplified Jouyban–Acree equation. The thermodynamic properties of the solution process, including the Gibbs energy, enthalpy, and entropy, were calculated by the van’t Hoff analysis.
Materials and apparatus
All solvents and N-Acetylglycine (Aladdin Chemistry Co., Ltd) used for experiments were of analytical reagent grade and their mass fraction purities were higher than 99%. More details about the purity of reagents are listed in Table 1. Analytical balance (model: BSA224S) was provided from Sartorius Scientific Instruments (Beijing) CO., Ltd. with an uncertainty of ± 0.0002 g. The smart Acetonitrile-circulator thermostatic bath (model: DC-2006) was provided by Ningbo Scientz Biotechnology Co. Ltd. with an uncertainty of ± 0.1 K.
| Compound | Provenance | Mass fraction purity |
|---|---|---|
| N-Acetylglycine | Aladdin Chemistry | 0.990 |
| Methanol | Aladdin Chemistry | 0.996 |
| Acetonitrile | Aladdin Chemistry | 0.991 |
Table 1: Provenance and purity of the materials used.
The solubility of N-Acetylglycine in methanol+Acetonitrile mixtures was determined from 278.15 K to 333.15 K at atmospheric pressure by the dynamic method [6-8]. Solvents and excess N-Acetylglycine were added into glass test tubes with stoppers. The glass test tubes were maintained at a double layer jacket glass equilibrium cell which was full of solution. The temperature of the inner was controlled by circulating which was from a smart Acetonitrilecirculator thermostatic bath. Stirring the mixture continuously uesed a magnetic stirrer for twentyfour hours until it reaching saturation andequilibrium. Then stop stirring to let the solution settle over nights to make sure the suspended solid precipitated. Next, took 1 mL the clear upper saturated solution by a pipette gun and transferred it into a 10 mL beaker with a cover that had been weighed up beforehand and then measured the total weight rapidly. Then the beaker was put into a dryer and the mass was recorded repeatedly until keeping the constant weight. Each experiment was repeated at least three times and we used the average value to calculate the mole fraction solubility at last. The mole fraction solubility of N-Acetylglycine (xI) in methanol+Acetonitrile is calculated by equation (1). The composition of solvent mixtures (xII) is defined using equation (2).
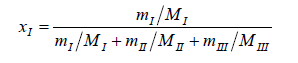 (1)
(1)
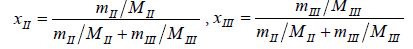 (2)
(2)
where mI, mII, mIIIrepresent the mass of the solute, methanol, Acetonitrile, and MI, MII, MIII represent the molecular weight of the solute, methanol, Acetonitrile, respectively.
Solubility data
The solubility data (xI) of N-Acetylglycine in methanol+Acetonitrile mixtures with the temperature ranging from 278.15 to 333.15 K are presented in Table 2. For comparison with each of the experimental points, experimental solubility data of N-Acetylglycine in methanol+Acetonitrile mixtures in the temperature range from 278.15 to 333.15 K are presented in Figures 3 and 4. From Table 2 and Figure 3, it can be found that the solubility of N-Acetylglycine in methanol+Acetonitrile mixtures is a function of temperature and solvent composition. More specifically, the solubility of N-Acetylglycine in Methanol+Acetonitrile mixtures increases with the rise of temperature, while at a constant temperature increases with increasing methanol content of the mixed solvent, By these properties, methanol could be used as effective benign solvent in the crystallization process.
| xII | 100xI | 100(xI -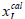 )/xI(Eq. 5) )/xI(Eq. 5) |
100(xI-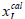 )/ xI(Eq. 6) )/ xI(Eq. 6) |
100(xI-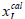 )/ xI(Eq. 9) )/ xI(Eq. 9) |
|---|---|---|---|---|
| T=278.15 K | ||||
| 0.000 | 0.322 | -0.086 | 0.000 | -1.266 |
| 0.090 | 0.326 | 0.168 | 0.221 | -0.042 |
| 0.194 | 0.330 | -0.013 | -0.057 | 1.249 |
| 0.315 | 0.336 | -0.088 | -0.091 | 0.098 |
| 0.458 | 0.343 | -0.091 | -0.074 | -0.140 |
| 0.628 | 0.352 | 0.197 | 0.194 | 0.097 |
| 0.835 | 0.364 | -0.116 | -0.119 | -0.032 |
| 1.000 | 0.384 | 0.029 | 0.000 | 0.004 |
| T=283.15 K | ||||
| 0.000 | 0.389 | 0.474 | 0.000 | -2.558 |
| 0.090 | 0.395 | -1.098 | -1.172 | -0.974 |
| 0.194 | 0.412 | 0.531 | 0.468 | 3.340 |
| 0.315 | 0.421 | 0.264 | 0.402 | 0.003 |
| 0.458 | 0.427 | 0.049 | 0.051 | -0.005 |
| 0.628 | 0.431 | -0.498 | -0.604 | 0.003 |
| 0.835 | 0.449 | 0.346 | 0.417 | -0.002 |
| 1.000 | 0.473 | -0.091 | 0.000 | 0.000 |
| T=288.15 K | ||||
| 0.000 | 0.457 | 0.472 | 0.000 | -2.649 |
| 0.090 | 0.465 | -1.093 | -1.023 | -0.975 |
| 0.194 | 0.484 | 0.530 | -0.569 | 3.421 |
| 0.315 | 0.513 | 0.265 | 1.501 | 0.015 |
| 0.458 | 0.521 | 0.039 | -0.110 | -0.021 |
| 0.628 | 0.527 | -0.483 | -1.012 | 0.016 |
| 0.835 | 0.549 | 0.338 | 0.707 | -0.005 |
| 1.000 | 0.579 | -0.089 | 0.000 | 0.001 |
| T=293.15 K | ||||
| 0.000 | 0.536 | 0.487 | 0.000 | -3.817 |
| 0.090 | 0.550 | -1.097 | -1.309 | -1.004 |
| 0.194 | 0.582 | 0.495 | 0.577 | 4.428 |
| 0.315 | 0.601 | 0.309 | 0.394 | 0.122 |
| 0.458 | 0.616 | -0.015 | -0.039 | -0.173 |
| 0.628 | 0.630 | -0.418 | -0.490 | 0.121 |
| 0.835 | 0.663 | 0.298 | 0.353 | -0.039 |
| 1.000 | 0.705 | -0.077 | 0.000 | 0.005 |
| T=298.15 K | ||||
| 0.000 | 0.638 | 0.438 | 0.000 | -3.746 |
| 0.090 | 0.646 | -0.952 | -1.406 | -0.875 |
| 0.194 | 0.673 | 0.342 | -0.872 | 4.238 |
| 0.315 | 0.728 | 0.399 | 2.863 | 0.172 |
| 0.458 | 0.724 | -0.072 | -1.743 | -0.244 |
| 0.628 | 0.764 | -0.373 | -0.069 | 0.171 |
| 0.835 | 0.803 | 0.275 | 0.375 | -0.055 |
| 1.000 | 0.856 | -0.072 | 0.000 | 0.007 |
| T=203.15 K | ||||
| 0.000 | 0.741 | 0.481 | 0.000 | -4.786 |
| 0.090 | 0.769 | -1.075 | -0.440 | -1.026 |
| 0.194 | 0.809 | 0.515 | 0.206 | 5.251 |
| 0.315 | 0.843 | 0.218 | -0.099 | 0.131 |
| 0.458 | 0.883 | 0.048 | 0.420 | -0.182 |
| 0.628 | 0.909 | -0.410 | -0.503 | 0.126 |
| 0.835 | 0.964 | 0.274 | 0.251 | -0.040 |
| 1.000 | 1.034 | -0.069 | 0.000 | 0.005 |
| T=308.15 K | ||||
| 0.000 | 0.876 | 0.501 | 0.000 | -4.998 |
| 0.090 | 0.910 | -1.100 | -0.543 | -1.082 |
| 0.194 | 0.954 | 0.511 | 0.023 | 5.489 |
| 0.315 | 1.002 | 0.182 | 0.876 | 0.071 |
| 0.458 | 1.025 | 0.155 | -0.982 | -0.098 |
| 0.628 | 1.090 | -0.506 | 0.443 | 0.068 |
| 0.835 | 1.159 | 0.314 | -0.098 | -0.021 |
| 1.000 | 1.245 | -0.078 | 0.000 | 0.004 |
| T=313.15 K | ||||
| 0.000 | 1.052 | 0.490 | 0.000 | -5.047 |
| 0.090 | 1.094 | -1.117 | 0.208 | -1.040 |
| 0.194 | 1.122 | 0.533 | -0.621 | 5.473 |
| 0.315 | 1.172 | 0.231 | 0.416 | 0.141 |
| 0.458 | 1.216 | 0.056 | 0.260 | -0.195 |
| 0.628 | 1.273 | -0.416 | -0.456 | 0.134 |
| 0.835 | 1.389 | 0.275 | 0.220 | -0.042 |
| 1.000 | 1.492 | -0.069 | 0.000 | 0.005 |
| T=318.15 K | ||||
| 0.000 | 1.212 | 0.024 | 0.000 | -2.710 |
| 0.090 | 1.241 | -0.053 | -0.757 | -0.281 |
| 0.194 | 1.311 | 0.186 | 0.790 | 2.975 |
| 0.315 | 1.353 | -0.553 | -0.433 | -0.500 |
| 0.458 | 1.423 | 0.760 | 0.249 | 0.678 |
| 0.628 | 1.480 | -0.531 | -0.197 | -0.453 |
| 0.835 | 1.592 | 0.190 | 0.097 | 0.134 |
| 1.000 | 1.782 | -0.036 | 0.000 | -0.015 |
| T=323.15 K | ||||
| 0.000 | 1.384 | -0.335 | 0.000 | -3.300 |
| 0.090 | 1.406 | 0.716 | 0.192 | 0.505 |
| 0.194 | 1.465 | -0.127 | -0.128 | 2.700 |
| 0.315 | 1.517 | -0.707 | -0.592 | -0.297 |
| 0.458 | 1.568 | 0.517 | 1.164 | 0.403 |
| 0.628 | 1.662 | -0.013 | -0.895 | -0.266 |
| 0.835 | 1.717 | -0.089 | 0.326 | 0.079 |
| 1.000 | 1.904 | 0.026 | 0.000 | -0.008 |
| T=328.15 K | ||||
| 0.000 | 1.673 | 0.033 | 0.000 | -3.006 |
| 0.090 | 1.723 | 0.052 | 0.043 | -0.024 |
| 0.194 | 1.776 | -0.181 | -0.178 | 2.962 |
| 0.315 | 1.843 | -0.164 | -0.156 | -0.365 |
| 0.458 | 1.941 | 0.660 | 0.652 | 0.495 |
| 0.628 | 2.032 | -0.601 | -0.599 | -0.327 |
| 0.835 | 2.254 | 0.240 | 0.240 | 0.095 |
| 1.000 | 2.516 | -0.048 | 0.000 | -0.010 |
| T=333.15 K | ||||
| 0.000 | 1.982 | -0.042 | 0.000 | -2.843 |
| 0.090 | 2.043 | 0.108 | 0.693 | -0.110 |
| 0.194 | 2.085 | 0.063 | -0.345 | 2.782 |
| 0.315 | 2.163 | -0.501 | -0.434 | 0.044 |
| 0.458 | 2.283 | 0.677 | 0.514 | -0.060 |
| 0.628 | 2.399 | -0.432 | -0.164 | 0.040 |
| 0.835 | 2.636 | 0.142 | -0.001 | -0.011 |
| 1.000 | 2.975 | -0.026 | 0.000 | 0.001 |
aStandard uncertainties u are u(T)=0.1K, u(xI)=0.0002, u(p)=0.02
Table 2: Calculation results of melting heat for b.c.c. lattices.
Data correction
The relationship of the experimental isothermal mole fraction solubility and binary solvent compositions is described by the Combined Nearly Ideal Binary Solvent /Redlich-Kister (CNIBS/R-K) model [9-11]. The model is presented in equation (3).
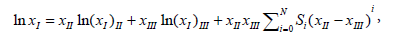 (3)
(3)
Where xII and xIII represent the initial mole fraction composition of the binary solvent when the solute was not added. Si is the model constant and the value of N can be 0, 1, 2 and 3. (xI)i represents the saturated mole fraction solubility of the solute(N-Acetylglycine) in pure solvent i. When N=2 and substitution of (1− xII) for xIII, then equation (3) can be converted into equation (4).
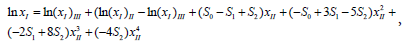 (4)
(4)
Which can be further simplified as the following equation:
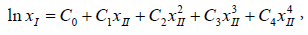 (5)
(5)
where C0, C1, C2, C3, C4 are model constants and we can get these constants by least-squares analysis [12].
Equation (5) is just variant one of CNIBS/R–K model. When N=2 and xIII is relaced by (1−xII), equation (3) can rearrangements result in equation (6).
This is variant two of CNIBS/R–K model [10]. The parameters Si would be obtained by regressing
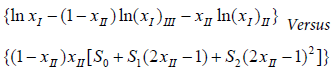 (6)
(6)
The CNIBS/R-K model only can be used to describe the solubility data and to predict solubility data for different concentrations of a mixed solvent at a fixed temperature. To describe the effect of both solvent compositions and temperature on the solubility of N-Acetylglycine, another model called Jouyban-Acree model was adopted [12,13]
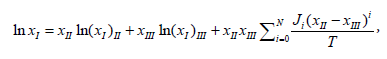 (7)
(7)
where Ji is the model constant, T is the absolute temperature, and other symbols denote the same meaning as equation (3). When N=2 and xIII is relaced by (1− xII) in equation (7), we can obtain equation (8) after rearrangement.
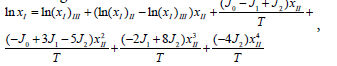 (8)
(8)
Equation (8) can also be further simplified as another form:
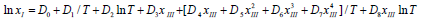 (9)
(9)
where D0, D1, D2, D3, D4, D5, D6, D7, D8 are parameters of this model.
Experimental solubility data of N-Acetylglycine were correlated with equation (5), equation (6) and equation (9). Calculated solubility data ( 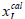 ) from these models are listed in Table 2.
) from these models are listed in Table 2.
The mean deviation (MD) [14,15] used as the validity of the models is introduced and calculated by equation (10):
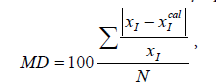 (10)
(10)
where N is the number of experimental points, xI is the experimental solubility and 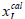 is the calculated solubility. The parameter values of equation (5), equation (6) and equation (9) are listed in Tables 3-5 together with the values of MD.
is the calculated solubility. The parameter values of equation (5), equation (6) and equation (9) are listed in Tables 3-5 together with the values of MD.
| T/K | C0 | C1 | C2 | C3 | C4 | MD |
|---|---|---|---|---|---|---|
| 278.15 | -5.738 | 0.080 | 0.349 | -0.665 | 0.412 | 0.099 |
| 283.15 | -5.555 | 0.387 | -0.469 | 0.129 | 0.154 | 0.419 |
| 288.15 | -5.358 | 0.396 | -0.466 | 0.107 | 0.170 | 0.514 |
| 293.15 | -5.235 | 0.529 | -0.566 | 0.138 | 0.180 | 0.399 |
| 298.15 | -5.042 | 0.507 | -0.469 | 0.001 | 0.243 | 0.665 |
| 303.15 | -4.910 | 0.632 | -0.627 | 0.128 | 0.205 | 0.486 |
| 308.15 | -4.742 | 0.648 | -0.562 | 0.004 | 0.267 | 0.419 |
| 313.15 | -4.559 | 0.663 | -0.662 | 0.158 | 0.195 | 0.399 |
| 318.15 | -4.413 | 0.256 | 0.251 | -0.612 | 0.492 | 0.391 |
| 323.15 | -4.261 | 0.296 | 0.062 | -0.362 | 0.412 | 0.316 |
| 328.15 | -4.091 | 0.327 | -0.030 | -0.106 | 0.219 | 0.248 |
| 333.15 | -3.896 | 0.321 | -0.239 | 0.261 | 0.039 | 0.249 |
| Overall | MD=0.384 |
Table 3: Parameters the variant 1 of CNIBS/R-K equation for N-Acetylglycine in Methanol+Acetonitrile binary solvent mixtures at the temperature range from (278.15 to 333.15) K.
| T/K | S0 | S1 | S2 | MD |
|---|---|---|---|---|
| 278.15 | -0.073 | -0.083 | -0.091 | 0.095 |
| 283.15 | -0.001 | -0.204 | -0.067 | 0.389 |
| 288.15 | 0.085 | -0.191 | -0.234 | 0.615 |
| 293.15 | 0.039 | -0.228 | -0.068 | 0.395 |
| 298.15 | 0.030 | -0.123 | -0.187 | 0.916 |
| 303.15 | 0.059 | -0.198 | -0.122 | 0.240 |
| 308.15 | 0.011 | -0.152 | 0.003 | 0.371 |
| 313.15 | -0.082 | -0.109 | 0.082 | 0.273 |
| 318.15 | -0.094 | -0.250 | -0.231 | 0.315 |
| 323.15 | -0.151 | -0.233 | -0.020 | 0.412 |
| 328.15 | -0.194 | -0.164 | -0.054 | 0.234 |
| 333.15 | -0.214 | -0.174 | -0.137 | 0.269 |
| Overall | MD= 0.377 |
Table 4: Parameters the variant 2 of CNIBS/R-K equation for N-Acetylglycine in Methanol+Acetonitrile binary solvent mixtures at the temperature range from (278.15 to 333.15) K.
| T/K | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | MD |
|---|---|---|---|---|---|---|---|---|---|---|
| 278.15 | 0.366 | |||||||||
| 283.15 | 0.861 | |||||||||
| 288.15 | 0.888 | |||||||||
| 293.15 | 1.214 | |||||||||
| 298.15 | 1.188 | |||||||||
| 303.15 | 1.443 | |||||||||
| 308.15 | 1.479 | |||||||||
| 313.15 | 1.510 | |||||||||
| 318.15 | 0.968 | |||||||||
| 323.15 | 0.945 | |||||||||
| 328.15 | 0.911 | |||||||||
| 333.15 | 0.736 | |||||||||
| -1.281 | -61.475 | -6.620 | -0.070 | 6.742 | 11.842 | 15.437 | 9.908 | 1.191 | ||
| Overall | MD=1.042 |
Table 5: Parameters of the Jouyban-Acree equation for N-Acetylglycine in Methanol+Acetonitrile binary solvent mixtures at the temperature range from (278.15 to 333.15) K.
As we can see from Tables 3-5, obtained overall MD value for the variant 1 of CNIBS/R-K equation is 0.384, for the variant 2 of CNIBS/ R-K equation is 0.377, and for the Jouyban-Acree equation is 1.042. This result indicated that the experimental data agreed well with the calculated results from the three equations, and the the variant 2 of CNIBS/R-K equation provided the more accurate prediction according to its lower value of the overall MD. The CNIBS/R-K equation can only be used for the prediction of solubility for different concentrations of a mixed solvent at constant temperature, while the Jouyban-Acree equation can be used for predicting solubility at different temperatures and different concentrations.
Thermodynamic analysis of dissolution
We can calculate the standard molar enthalpy of dissolution (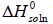 ) from the slope of the lnxI versus 1/T plot by equation (11). This is the van’t Hoff analysis and it is defined as [16-18]:
) from the slope of the lnxI versus 1/T plot by equation (11). This is the van’t Hoff analysis and it is defined as [16-18]:
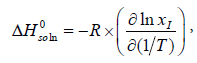 (11)
(11)
The standard molar enthalpy of dissolution (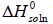 ) would be valid for the mean temperature ( Tmean=305.65 K, in the present work) in a certain temperature range. Equation (11) can also be represented as:
) would be valid for the mean temperature ( Tmean=305.65 K, in the present work) in a certain temperature range. Equation (11) can also be represented as:
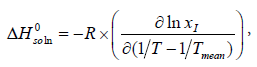 (12)
(12)
In addition, we can also calculate the standard molar Gibbs energy of dissolution (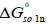 ) according to [19]:
) according to [19]:
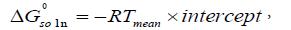 (13)
(13)
where the intercept is obtained in plots of lnxI versus (1/T-1/Tmean).
Then the standard molar entropy of dissolution ( 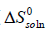 ) is calculated by [20]:
) is calculated by [20]:
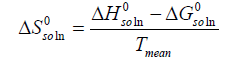 (14)
(14)
The calculation results of the standard Gibbs energy, enthalpy, and entropy are shown in Tables 6 together with ξTS and ξH. The ξTS and ξH is the comparison of the relative contribution to the standard Gibbs energy by enthalpy and entropy in the dissolution process, respectively.
| xII | 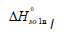 /KJ·mol-1 /KJ·mol-1 |
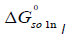 /KJ·mol-1 /KJ·mol-1 |
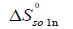 /J·mol-1·K-1 /J·mol-1·K-1 |
%ξH | %ξTS |
|---|---|---|---|---|---|
| 0.000 | 22.869 | 12.381 | 34.944 | 68.558 | 31.442 |
| 0.090 | 23.270 | 12.314 | 36.503 | 67.989 | 32.011 |
| 0.194 | 23.494 | 12.212 | 37.587 | 67.559 | 32.441 |
| 0.315 | 23.671 | 12.110 | 38.516 | 67.187 | 32.813 |
| 0.458 | 24.266 | 12.038 | 40.739 | 66.493 | 33.507 |
| 0.628 | 24.713 | 11.954 | 42.509 | 65.951 | 34.049 |
| 0.835 | 25.648 | 11.802 | 46.128 | 64.942 | 35.058 |
| 1.000 | 26.508 | 11.621 | 49.596 | 64.038 | 35.962 |
Table 6: Thermodynamic functions relative to solution process of N-Acetylglycine in Methanol+Acetonitrile binary solvent mixtures at mean temperature.
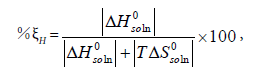 (15)
(15)
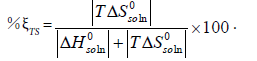 (16)
(16)
We can conclude from Table 6 that the standard Gibbs energy and the enthalpy of N-Acetylglycine are positive in the selected binary solvent mixtures, so it means the dissolution process of N-Acetylglycine in Methanol+Acetonitrile is endothermic. Furthermore, the main contributor to the standard molar Gibbs energy of solution is the enthalpy during the dissolution in virtue of values of %ξH are ≥ 64.038 for Methanol+Acetonitrile.
In this work new data were provided for the solubility of N-Acetylglycine in Methanol+Acetonitrile mixtures at temperature range from 278.15 K to 333.15 K. We can draw the following conclusions: The solubility of N-Acetylglycine in Methanol+Acetonitrile mixtures increases with the rise of temperature, while at a constant temperature increased with increasing methanol content of the mixed solvent. The solubility data could be successfully correlated using the two variants of the combined nearly ideal binary solvent/Redlich–Kister (CNIBS/ R–K) equation and the Jouyban–Acree equation, but the variant 2 of CNIBS/R-K equation was more accurate than the other two equations. The thermodynamic properties for the dissolution process including Gibbs energy, enthalpy, and entropy were obtained by the van’t Hoff analysis. The enthalpy change and the standard Gibbs energy change are positive proved that the dissolution process of N-Acetylglycine in Methanol+Acetonitrile mixtures was endothermic and contributor to the standard molar Gibbs energy of solution was the enthalpy during the dissolution due to values of %ξH are ≥ 64.038. The experimental solubility data and the parameters could be used for optimizing the purification process of N-Acetylglycine in industry.
This research work was financially supported by the Science and Technology support program of JiangSu Province (Agriculture) (Grant No. BE2012373, BE2012374), the College Industrialization Project of Jiangsu Province (Grant No. JHB2011-16).