Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2016) Volume 0, Issue 0
With the aim to study the viscosity and density of acetronitrile with 2- ethoxyethanol and 2- butoxyethanol at temperatures 293K, 303K and 313K over the whole composition range. The experimental results were used to calculate deviation in viscosity (Δη), excess internal pressure ( E i π ) and excess enthalpy ( E m H ). These results are used to quantitatively discuss the nature of interaction taking place between the components when mixed in terms of hydrogen-bond effects, dipole-dipole interaction weak vanderwaals type dispersion force. The calculated quantities have been fitted to Redlich-Kister equation.
Keywords: Viscosity; Internal pressure; Excess enthalpy; Redlich Kister equation
Mixed solvents rather than single pure liquids, are extensively used in industrial process as they provide a wide range of solvent with variable physical properties. The physical property data on mixed solvents are important for the theoretical and applied areas of research and are frequently used in many chemical and industrial processes such as design of new process and process equipment (fluid flow, mass transfer or heat transfer calculation). Acetonitrile is used as a polar aprotic solvent in organic synthesis and in the purification of butadiene. In the laboratory, it is used as a medium-polarity solvent that is miscible with water and a range of organic solvents, but not saturated hydrocarbons. It has a convenient liquid range and a high dielectric constant of 38.8. With a dipole moment of 3.92 D. Acetonitrile plays a significant role as the dominant solvent used in the manufacture of DNA oligonucleotides from monomers. Industrially, it is used as a solvent for the manufacture of pharmaceuticals and photographic film. 2- ethoxyethanol is a versatile organic liquid used in chemical industries as a solvent for lacquers, oils, and resin and as an antifreeze for explosive. It is miscible with a number of organic solvents as well as water. 2-butoxyethanol is a solvent in paint and surface coatings, as well as cleaning products and inks. Other products that contains 2- butoxyethanol include acrylic resin formulation, asphalt release agents, firefighting foam, leather protectors, oil spill dispersants, lane degreases and photographic strip solutions. Other products containing 2-butoxyethanol as a primary ingredient include some whiteboard cleaners, liquid soaps, cosmetics, dry cleanings solutions, lacquers, varnishes, herbicides and latex paints.
Viscosity and density data are required in many chemical engineering calculations involving fluid flow, heat and mass transfer. Moreover, the knowledge of dependence of viscosity and density on mixture composition and temperature is of considerable interest in understanding the intermolecular interactions [1-6] Internal pressure has been a subject of active interest and attempts have been made to show the significance of internal pressure as a fundamental property [7]. The present study reports the experimental values of viscosity (η) for the binary mixture of acetonitrile with 2 ethoxyethanol and 2- butoxyethanol at temperatures 293K, 303K and 313K over the whole composition range. The experimental results were used to calculate deviation in viscosity (Δη), excess internal pressure (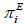 ) and excess enthalpy (
) and excess enthalpy (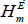 ). These results are used to quantitatively discuss the nature of interaction taking place between the components when mixed in terms of hydrogen-bond effects, dipole-dipole interaction weak vanderwaals type dispersion force. The calculated quantities have been fitted to Redlich – Kister equation [8].
). These results are used to quantitatively discuss the nature of interaction taking place between the components when mixed in terms of hydrogen-bond effects, dipole-dipole interaction weak vanderwaals type dispersion force. The calculated quantities have been fitted to Redlich – Kister equation [8].
Materials
The analytical grade chemicals Acetronitrile (Fluka), 2- ethoxyethanol (Sigma- Aldrich, ACS reagent, ≥ 99.5%) and 2- Butoxyethanol (Sigma- Aldrich, ACS reagent, ≥ 98.6%) have been obtained from Sigma Aldrich Chemicals Pvt. Ltd. All the chemicals were purified by standard procedure discussed by Perrin and Armarego [9]. Solutions have been prepared by mass, using air tight bottles and have been measured on electronic balance OHAUS- AR 2104 (Ohaus Corp. Pine Brook, NJ, USA) with an accuracy of 1 × 10-4 g. The possible error in the estimation of mole fraction is less than ± 0.0001.
Apparatus and procedures
The viscosities have been measured using Brookfield LVDVII+ Pro Programmable cone and plate viscometer (Brookfield Engineering Laboratories, Inc., USA). The experimental assembly allows measurement of viscosities in the range of 0.15 cP to 3065 cP (with spindle CPE-40) and 4.6 cP to 92130 cP (with spindle CPE- 52) with an accuracy of ± 1.0% of full scale range and repeatability of ± 0.2%. The apparatus requires only 0.5 ml of the mixture for measurement of viscosity. The apparatus measures fluid absolute viscosity directly in cP. The apparatus was calibrated by two viscosity standards Polydimethylsiloxane with viscosity 4.6 and 485 cP provided by Brookfield Engineering Laboratories. The viscosity standards are Newtonian, and therefore, have the same viscosity regardless to the spindle speed.
Circulating water bath with programmable temperature controller (TC-502, Brookfield Engineering Laboratories, Inc., USA), having variable pump speeds, has been used for water circulation in water jackets of the apparatuses. The temperature controller covers the temperature measurement range of -20°C to 200°C, with temperature stability of ± 0.01°C.
Structure of chemical compounds
The Figure 1 gives the structural information of the chemical compounds Acetronitrile (Fluka), 2- ethoxyethanol (Sigma- Aldrich, ACS reagent, ≥ 99.5%) and 2- Butoxyethanol (Sigma- Aldrich, ACS reagent, ≥ 98.6%).
Thermophysical parameters deviation in viscosity, excess internal energy and excess enthalpy were calculated from equations
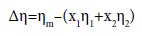 (1)
(1)
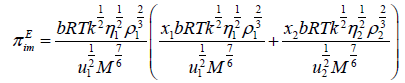 (2)
(2)
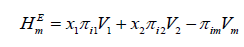 (3)
(3)
Experimental values of viscosity are given in Table 1 for binary mixture of acetonitrile + 2- ethoxyethanol and acetonitrile + 2- butoxyethanol at temperature 293K, 303K and 313K respectively. Deviation in viscosity (Δη), excess internal pressure (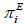 ) and excess molar enthalpy (
) and excess molar enthalpy (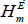 ) are given in Table 2, with the mole fraction of acetonitrile. Variations of respective parameters Δη ,
) are given in Table 2, with the mole fraction of acetonitrile. Variations of respective parameters Δη , and against mole fraction of acetonitrile (x1) are shown in Figures 2-4 respectively.
and against mole fraction of acetonitrile (x1) are shown in Figures 2-4 respectively.
| X1 | ηm(mPa.s) | ∆η(mPa.s) | (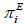 MPa) MPa) |
(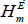 kJ.mol-1) kJ.mol-1) |
|---|---|---|---|---|
| 293K | ||||
| 0 | 2.084 | 0 | 0 | 0 |
| 0.1961 | 1.551 | -0.201 | -11.6365 | 1.3954 |
| 0.3544 | 1.216 | -0.2681 | -16.8876 | 1.8896 |
| 0.4848 | 0.979 | -0.2832 | -21.9262 | 2.141 |
| 0.5941 | 0.808 | -0.2693 | -25.7399 | 2.224 |
| 0.6871 | 0.676 | -0.2444 | -30.4327 | 2.341 |
| 0.7671 | 0.575 | -0.2091 | -33.4705 | 2.3421 |
| 0.8367 | 0.502 | -0.1644 | -32.6073 | 2.1159 |
| 0.8978 | 0.458 | -0.105 | -21.9008 | 1.3324 |
| 0.9518 | 0.419 | -0.0525 | -12.4416 | 0.7158 |
| 1 | 0.39 | 0 | 0 | 0 |
| 303K | ||||
| 0 | 1.67 | 0 | 0 | 0 |
| 0.1961 | 1.296 | -0.1148 | -4.7431 | 0.6106 |
| 0.3544 | 1.032 | -0.1697 | -10.4712 | 1.0882 |
| 0.4848 | 0.829 | -0.2005 | -20.4787 | 1.7154 |
| 0.5941 | 0.698 | -0.1871 | -21.9318 | 1.6606 |
| 0.6871 | 0.589 | -0.1732 | -26.5711 | 1.8587 |
| 0.7671 | 0.509 | -0.1474 | -27.8748 | 1.8126 |
| 0.8367 | 0.448 | -0.117 | -27.1662 | 1.6739 |
| 0.8978 | 0.406 | -0.078 | -20.5587 | 1.1868 |
| 0.9518 | 0.376 | -0.0368 | -9.815 | 0.5449 |
| 1 | 0.349 | 0 | 0 | 0 |
| 313K | ||||
| 0 | 1.341 | 0 | 0 | 0 |
| 0.1961 | 1.082 | -0.059 | -0.3634 | 0.0632 |
| 0.3544 | 0.882 | -0.0972 | -5.5194 | 0.3563 |
| 0.4848 | 0.716 | -0.129 | -16.5546 | 1.0958 |
| 0.5941 | 0.608 | -0.126 | -19.6978 | 1.2131 |
| 0.6871 | 0.52 | -0.1186 | -24.0431 | 1.4123 |
| 0.7671 | 0.458 | -0.099 | -23.2169 | 1.2942 |
| 0.8367 | 0.399 | -0.086 | -27.0576 | 1.5207 |
| 0.8978 | 0.368 | -0.055 | -18.2036 | 0.973 |
| 0.9518 | 0.341 | -0.027 | -9.308 | 0.4987 |
| 1 | 0.318 | 0 | 0 | 0 |
Table 1: Viscosity (ηm) deviation in viscosity (Δηm), excess internal pressure (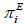 ) and excess molar enthalpy (
) and excess molar enthalpy (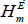 ) for acetonitrile+2-ethoxyethanol mixtures.
) for acetonitrile+2-ethoxyethanol mixtures.
| X1 | ηm(mPa.s) | ∆η(mPa.s) | 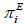 (MPa) (MPa) |
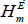 (kJ.mol-1) (kJ.mol-1) |
|---|---|---|---|---|
| 293K | ||||
| 0 | 3.126 | 0 | 0 | 0 |
| 0.2423 | 2.155 | -0.3081 | -11.0081 | 0.425 |
| 0.4185 | 1.497 | -0.4842 | -32.4926 | 2.1097 |
| 0.5523 | 1.134 | -0.4811 | -39.8633 | 2.3839 |
| 0.6573 | 0.892 | -0.4355 | -44.7111 | 2.5005 |
| 0.7422 | 0.714 | -0.3809 | -50.4412 | 2.7707 |
| 0.812 | 0.591 | -0.313 | -52.4877 | 2.7966 |
| 0.8704 | 0.519 | -0.2255 | -42.3732 | 2.1053 |
| 0.92 | 0.458 | -0.1504 | -34.0228 | 1.6355 |
| 0.9628 | 0.421 | -0.0705 | -16.889 | 0.7586 |
| 1 | 0.39 | 0 | 0 | 0 |
| 303K | ||||
| 0 | 2.43 | 0 | 0 | 0 |
| 0.2423 | 1.707 | -0.2186 | -14.7708 | 0.3631 |
| 0.4185 | 1.185 | -0.3746 | -42.0453 | 2.4124 |
| 0.5523 | 0.869 | -0.412 | -62.5906 | 3.7278 |
| 0.6573 | 0.699 | -0.3635 | -65.7516 | 3.6031 |
| 0.7422 | 0.592 | -0.2936 | -60.0033 | 2.9971 |
| 0.812 | 0.517 | -0.223 | -50.3727 | 2.2897 |
| 0.8704 | 0.452 | -0.1665 | -43.8708 | 1.939 |
| 0.92 | 0.413 | -0.1022 | -28.1809 | 1.128 |
| 0.9628 | 0.376 | -0.0501 | -15.5975 | 0.6142 |
| 1 | 0.349 | 0 | 0 | 0 |
| 313K | ||||
| 0 | 1.8977 | 0 | 0 | 0 |
| 0.2423 | 1.3685 | -0.1465 | -18.1925 | 0.2078 |
| 0.4185 | 0.9488 | -0.288 | -51.542 | 2.6503 |
| 0.5523 | 0.7156 | -0.3098 | -69.9963 | 3.6835 |
| 0.6573 | 0.5827 | -0.2769 | -74.3164 | 3.673 |
| 0.7422 | 0.5041 | -0.2215 | -67.3879 | 3.0109 |
| 0.812 | 0.4559 | -0.1594 | -51.6844 | 1.9755 |
| 0.8704 | 0.4042 | -0.1189 | -44.08 | 1.6493 |
| 0.92 | 0.3696 | -0.0751 | -30.1247 | 1.0614 |
| 0.9628 | 0.3433 | -0.0339 | -13.9832 | 0.4332 |
| 1 | 0.3184 | 0 | 0 | 0 |
Table 2: Viscosity (ηm), deviation in viscosity (Δηηm) excess internal pressure (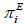 ) and deviation in molar enthalpy (
) and deviation in molar enthalpy (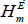 ) for acetonitrile+2-butoxyethanol mixtures.
) for acetonitrile+2-butoxyethanol mixtures.
Excess parameters
It has been reported by many workers [10-14] that three main types of contributions to excess thermodynamic properties of mixtures are:
(1) Physical: due to non-specific Vander Walls type interactions;
(2) Chemical: due to hydrogen bonding;
(3) Structural: due to changes of interstitial accommodation and free volume.
The study of excess parameters is very important in order to explain the various type of interaction occurring in binary mixtures.
Deviation in viscosity (Δη) is plotted against mole fraction of acetonitrile (x1) for both mixtures. Generally the positive values of deviation viscosity (Δη) indicate the predominance of hydrogen bonding interaction between unlike molecules over the dissociation effects of the mixing components [15]. It is known that the strength of the molecular hydrogen bonding is not only the factor influencing viscosity deviation (Δη) in the liquid mixture, the molecular size and shape of the components and average degree of association is equally important factor [16]. In the absence of strong specific interaction leading to complex formations, negative deviation generally occur when dispersive forces are primarily responsible for interaction or even when they interact more strongly via dipole – dipole interaction [17]. This also means that the interaction between pairs of like molecules is stronger than between pairs of unlike molecules. When temperature is increased then the values of deviation in viscosity (Δη) becomes less negative in case of both mixtures. It has been noticed from Figure 2 that deviation in viscosity (Δη) found to be negative for both mixtures. This negative deviation shows dispersive force is acting between unlike molecules of component mixtures. More negative values of (Δη) in case of acetonitrile + 2-butoxyethanol mixtures support our results.
It has been seen from Figure 4 that the values of excess internal pressure (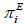 ) has found to be negative for both the systems at temperatures 293K, 303K and 313K over entire composition range. At around x1=0.7 maximum value is found shows the complex formation at this concentration. Excess negative values for both mixture show long range dispersive force operating between components mixture suggest that rupture of hydrogen bonding chain of 2- ethoxyethanol and 2- butoxyethanol is stronger than the hydrogen bonding between unlike molecules.
) has found to be negative for both the systems at temperatures 293K, 303K and 313K over entire composition range. At around x1=0.7 maximum value is found shows the complex formation at this concentration. Excess negative values for both mixture show long range dispersive force operating between components mixture suggest that rupture of hydrogen bonding chain of 2- ethoxyethanol and 2- butoxyethanol is stronger than the hydrogen bonding between unlike molecules.
Values of excess molar enthalpy (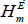 ) were found to be negative in the case of specific complex formation and positive in the case of dissociation. In our present study the values of excess molar enthalpy (
) were found to be negative in the case of specific complex formation and positive in the case of dissociation. In our present study the values of excess molar enthalpy (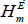 ) is found to be positive for both mixtures. Larger positive values in both mixtures suggest specific weak interaction between molecules of components mixtures. More positive values in case of acetonitrile +2-butoxyethanol suggest that long range dispersive force is prominent in this case. The trend of excess molar enthalpy (
) is found to be positive for both mixtures. Larger positive values in both mixtures suggest specific weak interaction between molecules of components mixtures. More positive values in case of acetonitrile +2-butoxyethanol suggest that long range dispersive force is prominent in this case. The trend of excess molar enthalpy (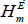 ) supports our earlier result of excess internal pressure (
) supports our earlier result of excess internal pressure (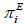 ).
).
Redlich-Kister polynomial equation data
The composition dependence of the excess properties is correlated by the Redlich-Kister polynomial equation. The values of excess parameters for each mixture were fitted to the Redlich- Kister polynomial equation of the type,
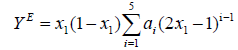 (4)
(4)
Where ai is the polynomial co-efficients.
The values of the co-efficients ai were obtained by the least squares method with all points weighted equally. In each case, the optimum number of co-efficients was ascertained from an examination of the variation of the standard deviation σ(YE) with no. of co-efficients (p).
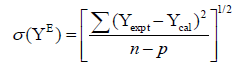 (5)
(5)
The values of co-efficient ai of Redlich – Kister polynomial equation evaluated using the method of least squares for the mixtures are given in Table 3 along with the standard deviation σ(YE).
| Parameters | Temp. (K) | α1 | α2 | α3 | α4 | α5 | σ(YE ) |
| acetonitrile+2-ethoxyethanol | |||||||
| Δη(mPa.s) | 293 | -1.1346 | -0.1909 | -0.5333 | 0.3178 | 0.7479 | 0.0016 |
| 303 | -0.9303 | -0.6333 | -0.297 | 1.964 | 1.8851 | 0.0016 | |
| 313 | -0.4816 | 0.1773 | -0.0073 | -0.0308 | 0.0794 | 0.0034 | |
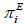 (MPa) (MPa) |
293 | -83.2904 | 81.3762 | -234.9172 | 79.8204 | 216.5565 | 1.1721 |
| 303 | -520.1019 | -1314.9 | 57.2027 | 3882.977 | 2908.0146 | 0.9995 | |
| 313 | -67.2473 | 117.49 | 132.2675 | -75.3104 | -278.3652 | 1.8347 | |
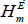 (kJ.mol-1) (kJ.mol-1) |
293 | 8.2279 | -2.8301 | 14.2574 | -3.901 | -15.3335 | 0.0753 |
| 303 | 29.8727 | 71.0567 | -1.845 | -208.4377 | -159.4172 | 0.0794 | |
| 313 | 4.3963 | -6.932 | -12.3042 | 7.2786 | 22.6867 | 0.1216 | |
| acetonitrile+2- butoxyethanol | |||||||
| Δη(mPa.s) | 293 | 0.0757 | 5.1174 | -4.3184 | -18.1271 | -10.9172 | 0.0087 |
| 303 | -1.6466 | 0.3884 | 1.6367 | -0.288 | -2.003 | 0.0028 | |
| 313 | 0.1883 | 5.2001 | -1.7859 | -17.401 | -11.7185 | 0.0163 | |
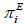 (MPa) (MPa) |
293 | -145.8562 | 81.8381 | -196.6476 | 492.6593 | 410.6228 | 1.6683 |
| 303 | -224.8594 | 293.2934 | 222.2356 | -239.4692 | -470.4946 | 1.5923 | |
| 313 | -250.5386 | 250.2075 | 36.5039 | 33.3339 | 104.8389 | 2.1697 | |
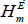 (kJ.mol-1) (kJ.mol-1) |
293 | 9.0466 | -1.6854 | 9.5056 | -40.8999 | -40.101 | 0.1112 |
| 303 | 13.4362 | -17.7698 | -27.2281 | 17.5737 | 35.9649 | 0.1082 | |
| 313 | 13.318 | -13.4031 | -16.5041 | -4.4572 | -3.2247 | 0.1418 | |
Table 3: Adjustable parameters αi with the standard deviations σ(YE) for deviation in viscosity (Δη) excess internal pressure (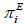 ) and excess molar enthalpy (
) and excess molar enthalpy (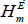 ) for both the binary mixtures at varying temperatures.
) for both the binary mixtures at varying temperatures.
Internal pressure
Internal pressure has been evaluated using empirical relations. A brief discussion of each empirical relation used is being given here.
Thermo dynamical relation: The relation among applied pressure (P), molar volume (V), temperature (T) and molar internal energy (U) is given by thermodynamic relation.
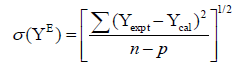
The isothermal internal energy-volume coefficient (∂Υ/∂V)Τ is often called internal pressure πi. Since α=1/V (∂V/∂Τ)P and kΤ=−1/V (∂V/∂P)Τ, the above equation, for the pressure limiting to zero, can be written as
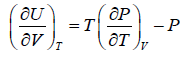 (6)
(6)
Relation using empirical equations for α and kΤ: From the empirical equations for thermal expansion coefficient α and isothermal compressibility kΤ [17] we get
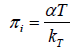 (7)
(7)
Relation based upon Buehler-Hirschfelder-Curtiss equation of state: With the help of equation proposed by Buehler et al. [18,19] the internal pressure can be given as
where V is the molar volume, d is the molecular diameter, T is the absolute temperature and R is the gas constant
Relation based upon Flory statistical theory: Knowing the thermal expansion coefficient α and isothermal compressibility kT of pure liquid components, the values of α and kT for liquid mixture can be evaluated as
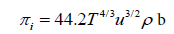
where V is the reduced volume, T is the absolute temperature and P* is the characteristic pressure. Using the values of α and kT thus obtained, one can evaluate the internal pressure of the liquid mixture using the relation [20].
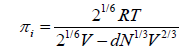
These relations have been applied to both the mixtures for the evaluation of internal pressure. The calculated values of internal pressure are given in Tables 4 and 5 respectively with average percentage deviation (APD) values. Here we have taken thermodynamic relation as reference because in this relation internal pressure has been evaluated from experimental data’s. By comparing APD values of each empirical formula we can say that empirical relations giving the best results for both binary mixtures at all three temperatures.
| X1 | Thermodynamic relation | Empirical relation | F. S. T. relation | B.H.C. relation |
|---|---|---|---|---|
| T=293K | ||||
| 0 | 387.1 | 387 | 387.1 | 380.3 |
| 0.1961 | 379.6 | 379.5 | 380.3 | 419 |
| 0.3544 | 372.4 | 372.3 | 373.4 | 455.5 |
| 0.4848 | 364.5 | 364.4 | 366.2 | 489.4 |
| 0.5941 | 356.5 | 356.4 | 358.9 | 521.5 |
| 0.6871 | 348.8 | 348.7 | 351.6 | 552.2 |
| 0.7671 | 341.4 | 341.3 | 344.2 | 581.6 |
| 0.8367 | 334.3 | 334.2 | 336.9 | 610 |
| 0.8978 | 327.4 | 327.3 | 329.6 | 637 |
| 0.9518 | 321.1 | 321.1 | 322.4 | 663.6 |
| 1 | 315.4 | 315.3 | 315.4 | 689.4 |
| APD | -0.024 | -0.466 | 58.41 | |
| T=303K | ||||
| 0 | 382 | 381.9 | 402.2 | 388.5 |
| 0.1961 | 375.8 | 375.7 | 395.4 | 428.3 |
| 0.3544 | 368.8 | 368.7 | 388.4 | 465.4 |
| 0.4848 | 360.8 | 360.7 | 381 | 499.8 |
| 0.5941 | 353.1 | 353.1 | 373.6 | 532.4 |
| 0.6871 | 345.9 | 345.9 | 366.2 | 563.9 |
| 0.7671 | 338.4 | 338.4 | 358.7 | 593.8 |
| 0.8367 | 331.4 | 331.4 | 351.2 | 622.6 |
| 0.8978 | 324.5 | 324.5 | 343.8 | 649.8 |
| 0.9518 | 318.2 | 318.2 | 336.5 | 676.4 |
| 1 | 311.9 | 311.9 | 329.2 | 701.9 |
| APD | -0.024 | 5.657 | 63.2 | |
| T=313K | ||||
| 0 | 375.8 | 375.7 | 375.8 | 396.1 |
| 0.1961 | 370.9 | 370.8 | 369.6 | 437.5 |
| 0.3544 | 363.7 | 363.6 | 363 | 474.7 |
| 0.4848 | 356.3 | 356.2 | 356.2 | 509.9 |
| 0.5941 | 349 | 348.9 | 349.3 | 543.3 |
| 0.6871 | 341.6 | 341.5 | 342.3 | 574.8 |
| 0.7671 | 334.5 | 334.4 | 335.3 | 605.1 |
| 0.8367 | 327.8 | 327.7 | 328.4 | 634.6 |
| 0.8978 | 321 | 320.9 | 321.5 | 662.3 |
| 0.9518 | 314.8 | 314.7 | 314.7 | 689.2 |
| 1 | 307.8 | 307.7 | 307.8 | 714 |
| APD 0.024 0.024 | 68.42 | |||
Table 4: Internal pressure of acetonitrile+2-ethoxyethanol mixture from various methods at T=293, 303, 313 K.
| X1 | Thermodynamic relation | Empirical relation | F. S. T. relation | B.H.C. relation |
|---|---|---|---|---|
| T=293K | ||||
| 0 | 372.8 | 372.8 | 372.8 | 282.3 |
| 0.2423 | 366 | 365.9 | 368.3 | 329.9 |
| 0.4185 | 359.4 | 359.3 | 363.3 | 375.7 |
| 0.5523 | 353 | 352.9 | 358 | 419.8 |
| 0.6573 | 346.6 | 346.5 | 352.3 | 461.9 |
| 0.7422 | 340.8 | 340.7 | 346.4 | 503 |
| 0.812 | 335.2 | 335.1 | 340.3 | 542.5 |
| 0.8704 | 329.8 | 329.7 | 334.2 | 580.8 |
| 0.92 | 324.8 | 324.7 | 327.9 | 618 |
| 0.9628 | 319.9 | 319.9 | 321.7 | 654.2 |
| 1 | 315.4 | 315.3 | 315.4 | 689.4 |
| APD | -0.024 | 0.9833 | 47.42 | |
| T=303K | ||||
| 0 | 372.5 | 372.4 | 372.5 | 288.5 |
| 0.2423 | 365 | 364.9 | 368.6 | 425.4 |
| 0.4185 | 357.9 | 357.8 | 364.2 | 470.6 |
| 0.5523 | 351.2 | 351.1 | 359.3 | 510.9 |
| 0.6573 | 344.7 | 344.6 | 354 | 547.2 |
| 0.7422 | 338.6 | 338.5 | 348.1 | 580.2 |
| 0.812 | 332.8 | 332.8 | 341.9 | 609.7 |
| 0.8704 | 327.2 | 327.1 | 335.1 | 636.4 |
| 0.92 | 322.1 | 322 | 327.9 | 660.5 |
| 0.9628 | 317 | 316.9 | 320.2 | 682.4 |
| 1 | 311.9 | 311.9 | 311.9 | 701.9 |
| APD | -0.024 | 1.683 | 65.83 | |
| T=313K | ||||
| 0 | 375.8 | 375.7 | 375.8 | 396.1 |
| 0.2423 | 370.9 | 370.8 | 369.6 | 437.5 |
| 0.4185 | 363.7 | 363.6 | 363 | 474.7 |
| 0.5523 | 356.3 | 356.2 | 356.2 | 509.9 |
| 0.6573 | 349 | 348.9 | 349.3 | 543.3 |
| 0.7422 | 341.6 | 341.5 | 342.3 | 574.8 |
| 0.812 | 334.5 | 334.4 | 335.3 | 605.1 |
| 0.8704 | 327.8 | 327.7 | 328.4 | 634.6 |
| 0.92 | 321 | 320.9 | 321.5 | 662.3 |
| 0.9628 | 314.8 | 314.7 | 314.7 | 689.2 |
| 1 | 307.8 | 307.7 | 307.8 | 714 |
| APD | -0.024 | 1.923 | 55.36 | |
Table 5: Internal pressure of acetonitrile+2-butoxyethanol mixture from various methods at T=293, 303, 313 K.
The observed values and their excess parameters suggest weak dipole-dipole interaction and dispersive force may contribute in result of viscosity, internal pressure and molar enthalpy and their excess values.
One of the authors (Sangeeta Sagar) thankful to UGC for providing financial support through Rajiv Gandhi National Fellowship.