Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2010) Volume 1, Issue 1
The pharmacological characteristics of a partial agonist, namely its binding and efficacy, are transposed, here, to give more insight into the mode of binding of the requisite agonist and antagonist bound complexes. Simple proportionality relationships of the efficacy to the overall binding define the agonist and antagonist binding constants. The advantage of such description lies in determining the thermodynamic profiles of the respective complexes by simple temperature variation. The enthalpic difference between agonist and antagonist complexes becomes a function of the efficacy, e alone, the thermodynamic scale ratio, e / (1-e), yielding this value directly. The concentration-response theory for two bound ligand conformer complexes, one of which yields an agonist response is examined using a simple adaptation of the Black and Leff model of agonism. A selected tissue response, the chronotropic in guinea-pig right atria, dominated by a single receptor, the β1 -adrenergic under normal signal amplification conditions, was selected. The chronotropic response accurately obeys a hyperbolic dose-response form, a condition for the model’s applicability and component profiles are exemplified at 30.0°C. The precision was found sufficient to evaluate the thermodynamics of the respective complexes over a 15°C range of temperature. in a second paper.
Keywords: Thermodynamics, Efficacy; Agonist; Antagonist binding enthalpies; Black and leff model; Partial agonism.
A partial agonist on a defined receptor may be viewed as arising primarily from the binding of two or more bound ligand conformer complexes, one of which activates an agonist response. For partial agonists obeying a hyperbolic dose-response relation, the two characteristic parameters of binding and efficacy may obviously be transposed to consider the binding of two effective bound conformer complexes while temperature studies should yield the characteristic thermodynamics associated with the binding of the respective agonist and antagonist components. For any determination ‘in vitro’, it is crucial that the particular tissue response is dominated by a single receptor sub-type and we have selected the cardiac chronotropic response of the β1-adrenergic receptor for study. Chronotropic responses to β-adrenergic stimulation in guinea pig right atria were early identified to be dominated by the β1-adrenergic receptor under normal conditions of signal amplification and this evidence is later reviewed. In this first paper, concentration-response theory is examined for the binding of two bound complexes and the appropriate conformer binding constants exemplified with chronotropic data on the partial agonist, prenalterol, at 30.0°C. In a second paper, the data are extended from 25.0°C to 40.0°C and the thermodynamic properties of the agonist complex compared with comparable data on full agonists. The enthalpic difference between agonist and antagonist complexes is determined and supports the development of a basic criterion for the onset of agonist action. We begin by reviewing the treatment of agonism in concentrationresponse theory.
Drug-receptor theory and agonism
The adsorption isotherm of Langmuir [1] is a natural model for describing concentration--response relationships in hormone and drug-receptor interactions. Where molecules are adsorbed onto single receptor sites and do not interact with each other, the fraction of sites occupied by a molecular species may be simply evaluated by using the law of mass action. A considerable range of hormonereceptor interactions for proteins of the G-protein-coupled receptors have dose-response relations not detectably different from the hyperbolic form of this model (for a review see [2]) and the binding constants of inhibitory agents on these receptors (antagonists) may be readily evaluated by simple competitive challenge of the agonist stimulant response [3,4,5].
Binding constants of agonists must be estimated by less direct methods for the relations between receptor occupancy and response are not in general known. Although the dose–response relationship for an agonist is often of hyperbolic form, this relation is not only a function of the drug or hormone but of the receptor and its associated mechanisms of signalling. It has long been recognized that signal amplification may follow receptor occupation to produce the response and that the response may not be directly proportional to occupancy. Stephenson [6] proposed that receptor occupancy could be related in a non-linear manner to a stimulus, the relationship being described by the efficacy (e) while the response was some further undefined function of the stimulus (f). This amplification of signal implied the concept of receptor reserve with only a fraction of the bound sites being required to sustain a full response [7] but unfortunately implied that the dose-response relation might not be of true Langmuir (hyperbolic) type.
To separate effects attributable to the drug-receptor mechanism from those of the signal amplification, Furchgott [8] scaled the efficacy with the total number of receptors available and defined the term, the intrinsic efficacy (ε). Thus
e = ε [RT ] (1)
where RT is the total number of receptors available. The fractional response E could then be written

where KA is the binding constant of A. The factors dependent on the tissue were, therefore, defined by the stimulus-response function f and RT, while the drug related factors were KA and ε. Furchgott and Burstyn [9] emphasized that both the binding constant and the intrinsic efficacy must be utilized in any comprehensive model of drug-receptor mechanism. The difficulty in this representation, however, still lies with the undefined form of the function f so that in practice only relative intrinsic efficacies are obtainable with effective cancellation of the unknown.
The fact that a wide range of agonist receptor interactions have dose-response relations closely identifiable with hyperbolic form led to the development of an operational model of pharmacological agonism [2]. In this model, one amplifying function ( ) replaces the efficacy and stimulus function. The subsequent interactions of the drug-receptor complex producing the response are modelled using simple mass action relations and appropriate binding constants. The hyperbolic concentration-response form is retained with one binding constant (KE) being used to define an effective amplifying interaction, this single transducer function
) replaces the efficacy and stimulus function. The subsequent interactions of the drug-receptor complex producing the response are modelled using simple mass action relations and appropriate binding constants. The hyperbolic concentration-response form is retained with one binding constant (KE) being used to define an effective amplifying interaction, this single transducer function  being dependent on KE and the total number of receptors. An absolute value of the amplification factor
being dependent on KE and the total number of receptors. An absolute value of the amplification factor  and a gross binding constant KA are thus utilised in this model.
and a gross binding constant KA are thus utilised in this model.
It is implicit in the general Black and Leff model that the binding of the agonist to the receptor and each stage of the resulting interactions of the bound complex (or any 1:1 products) may be treated in relative isolation. This condition gives the characteristic form of the Langmuir hyperbolic relation for the requisite stage of the amplifying process by simple considerations of the relevant fractions of the bound and unbound molecular system. In equilibrium conditions, however, all relevant fractions of complexes containing R may be pertinent. In the case of the ternary complex of agonist, receptor and amplifying unit, if the total concentration, RT greatly exceeds that of the amplifying units, ET, the hyperbolic dose-response form is obtained [2]. This is also true for the reverse condition where ET >>RT and  is then a function of ET [10,11,12]. The most general model involving the given equilibria between receptor amplifying unit and agonist is, however cooperative in form [13] and a more specific model of agonist, receptor and amplifying unit has also been given [14]. The relation between classical and cooperative models has been reviewed [15]. A more general model for defining the interactions of receptor, ligand and G protein is the cubic ternary complex model [16,17] where the vertices represent the appropriate species defining the ligand, receptor and G protein but where the receptor can be in active and inactive forms. This model points out the multiplicity of bound species which might contribute to the measurement of affinity on signal activation but some more precise physical definition is required to gain insight into potential ligand-receptor activation. We have utilised this representation to consider the steady state equations for receptor activation by ligand protonation of the receptor leading to activation of phosphate transfer in an early GTP synthase model. [18]. The steady state equations could not, however, distinguish between a GTP synthase and a GDP/GTP exchange mechanism. While the precise details of a potential acid-base-acid proton shuttle mechanism were not correct, it was shown under steady state conditions that an increased rate of hydrogen ion diffusion into a receptor mutant could give rise to constitutive activity while increased rates of G protein release and changes in receptor state balance could contribute to the resultant level of action. Constitutive action could arise from a faster rate of G protein release alone if proton diffusion in the wild type receptor contributed to a basal level of G protein activation. Thus simple equilibria affecting activation of ternary complexes could be equated with given molecular species but further progress was only likely by understanding the role of more detailed molecular determinants of the ligand and receptor.
is then a function of ET [10,11,12]. The most general model involving the given equilibria between receptor amplifying unit and agonist is, however cooperative in form [13] and a more specific model of agonist, receptor and amplifying unit has also been given [14]. The relation between classical and cooperative models has been reviewed [15]. A more general model for defining the interactions of receptor, ligand and G protein is the cubic ternary complex model [16,17] where the vertices represent the appropriate species defining the ligand, receptor and G protein but where the receptor can be in active and inactive forms. This model points out the multiplicity of bound species which might contribute to the measurement of affinity on signal activation but some more precise physical definition is required to gain insight into potential ligand-receptor activation. We have utilised this representation to consider the steady state equations for receptor activation by ligand protonation of the receptor leading to activation of phosphate transfer in an early GTP synthase model. [18]. The steady state equations could not, however, distinguish between a GTP synthase and a GDP/GTP exchange mechanism. While the precise details of a potential acid-base-acid proton shuttle mechanism were not correct, it was shown under steady state conditions that an increased rate of hydrogen ion diffusion into a receptor mutant could give rise to constitutive activity while increased rates of G protein release and changes in receptor state balance could contribute to the resultant level of action. Constitutive action could arise from a faster rate of G protein release alone if proton diffusion in the wild type receptor contributed to a basal level of G protein activation. Thus simple equilibria affecting activation of ternary complexes could be equated with given molecular species but further progress was only likely by understanding the role of more detailed molecular determinants of the ligand and receptor.
An analysis of β1-adrenoceptor partial agonists showed that the degree of agonism of a set of phenoxypropanolamine partial agonists could be associated with a contraction of the ligand even though the comparative gross binding constants (dominated by the antagonist binding) of the ligands appeared constant to within ± 0.15 kcal/mol. when referenced to a simple hydrophobic environment [19]. A minor deformed conformer lying within one known antagonist conformation appeared the most likely agonist species which, coupled with signal amplification created the response. This raised the question of defining agonist and antagonist components of binding as an explicit conformer representation and whether the two parameters of efficacy and gross binding might give more insight if transformed into two parameters associated with the binding of two conformers, one representing the specific agonist conformer with an associated signal amplification and the other, the more generalised conformation representing the antagonist action or the sum of its components. The driving force for this representation arose from the early observation of Molinoff and co-workers [20] that the thermodynamic binding functions of ethanolamine agonists and phenoxypropanolamine partial agonists and antagonists on β-adrenoceptors have very widely differing characteristics, there being an unusual highly favourable - 5-6 kcal/mol TΔS entropy contribution for antagonist binding of phenoxypropanolamine compounds compared with a small unfavourable entropy contribution in the binding of the ethanolamine agonist, adrenaline although the free energies of binding are similar. The simple observation that partial agonists at β1-adrenoceptors come closer to full agonists on dropping the temperature [21] is obviously supportive of these results with the high binding enthalpy associated with agonist action.
In this first paper, examining the description required for the binding of partial agonists on the β1-adrenergic receptor, we adapt concentration-response theory for separate binding constants associated with agonist and antagonist complexes using a conformer description and develop the requisite binding constants at 30.0°C for the action of the phenoxypropanolamine partial agonist, prenalterol [3-(4-hydroxyphenoxy) 1-isopropylamino propan-2-ol] on the guineapig right atrium. We consider the accuracy of the unit slope relation in the hyperbolic response to indicate any constraints on a non-selective response from β2-adrenergic receptors and utilising evidence on selective agonists and antagonists, estimate the response dominance of the β1-receptor to be greater than 95% under normal signalling conditions. We examine the nature of the parameter  and consider whether variations in this amplification factor can arise between full agonists and partial agonists and the resultant form of the response if the amplification signals are competitive or independent. The latter condition for action within a particular receptor site appears unlikely unless a secondary action not directly relatable to the primary effect is present in the binding and will be given only limited consideration. In a second paper we determine the thermodynamic data for the agonist and antagonist binding components of prenalterol binding to the β1-adrenergic receptor using the competitive model for signal amplification. From comparative extrathermodynamic data on this receptor, we go on to determine whether there is a potential contraction in the prenalterol agonist conformer on binding and what conclusions may be drawn on the criteria for agonist action. We examine the compatibility of the proposed conformer interactions of the ligand with specific receptor residues regulating a proposed proton signalling mechanism involving a phosphate transfer within a G protein ternary complex [22].
and consider whether variations in this amplification factor can arise between full agonists and partial agonists and the resultant form of the response if the amplification signals are competitive or independent. The latter condition for action within a particular receptor site appears unlikely unless a secondary action not directly relatable to the primary effect is present in the binding and will be given only limited consideration. In a second paper we determine the thermodynamic data for the agonist and antagonist binding components of prenalterol binding to the β1-adrenergic receptor using the competitive model for signal amplification. From comparative extrathermodynamic data on this receptor, we go on to determine whether there is a potential contraction in the prenalterol agonist conformer on binding and what conclusions may be drawn on the criteria for agonist action. We examine the compatibility of the proposed conformer interactions of the ligand with specific receptor residues regulating a proposed proton signalling mechanism involving a phosphate transfer within a G protein ternary complex [22].
Drug-receptor theory for bound conformers in partial agonism
It is an obvious consequence of partial agonism that only a fraction of the bound drug-receptor complexes can produce the response. As drug molecules do not normally exist in rigid form but are vibrating deformable entities, a logical extension to the definition of partial agonism is that two or more bound conformer interactions occur in partial agonism, one of which (at least) must initiate a stimulus response. The fact that such bound drug-receptor conformers may have no separate unbound existence does not invalidate their pharmacological definition. Thermodynamic functions can obviously be associated with such forms which should be accessible by theoretical chemistry. The theoretical unbound equivalent forms, however, represent the ideal conformation for maximum interaction with the receptor in the given binding mode.
The relations of observed thermodynamic binding functions to their conformer representationa have been given elsewhere [23]. Binding constants for complex formation are used in preference to the reciprocal dissociation constants for manipulative convenience in Langmuir hyperbolic relations.
Conformer binding constants. some definitions
Using BR, B and R to define complex, drug and receptor respectively with indices to identify the conformer i of the drug engaged in binding with jx its receptor counterpart, then the simple mass action relations may be written for the conformer interactions

Using the conformer binding constants, Kijx….Krsx where
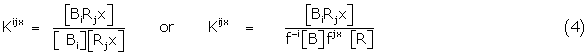
and the concentrations of Bi and Rjx are given in terms of the total concentrations of B and R and their respective conformer fractions fi and fjx respectively.
Rearranging (4)

and since the total concentration of the bound complex is given by Σi Σjx [Bi Rjx], then the gross binding constant, K is given by
K = Σi Σjx fi fjx Kijx
= Σi Σjx Kijx o (6)
where the subscripto is used for summarising the composite form of the binding constant in (6).
Since we cannot learn about fi and fjx except by extrathermodynamic comparisons [22], it is more convenient to redefine the binding constants referenced to the total concentrations of B and R respectively. In practice, this is simply rewriting (5) without the appropriate conformer fractions on the left hand side of the equation and dropping the subscript o, the sum of these binding constants, Kijx, representing the composite form of (6). This merely transposes the binding constants relative to the total concentrations of B and R. In the thermodynamic representation of (6), the observed standard free energy change associated with the complex formation can then be written
ΔGØ = - RT log K
= - RT ∼i Σjx pBiRjx log Kijx
+ RT Σi Σjx pBiRjx log pBiRjx (7)
where the p’s represent the appropriate conformer fractions of the bound ligands.
The transformation of gross binding and efficacy into two separate binding parameters related to agonist and antagonist action may, therefore, throw light on the associated thermodynamics differences in the binding constants of agonist and antagonist complexes but relative to the gross concentrations of ligand and receptor. For a partial agonist B, two binding constants Kijx and Krsx will be used to define primary agonist and antagonist conformer interactions. The antagonist interactions may be readily expanded in a more general definition. It should be emphasized that the dimensions of i, r, jx and sx are governed by the bound conformer dimensions defining the respective bound complexes and that the sole constraint to these dimensions is that ijx ≠ rsx although, under given conditions, i may equal r or jx may equal sx.
Response as a linear function of receptor occupancy: For a partial agonist B, it is convenient to examine initially, the linear relation between receptor occupancy and response for the case of two bound conformers as defined above. It may be shown that whether using the agonist response directly or by challenging a full agonist response with the partial agonist, an exact gross binding constant KB is obtained. The maximal stimulatory response and the gross binding constant permit separate evaluation of the agonist and antagonist binding constants Kijx and Krsx.
Without differentiation of conformers, the fractional agonist response of the partial agonist R(B) is directly proportional to the fraction of sites y(B) occupied by B and

Where eB may be defined as the efficacy of B within the linear model.
In the case of the two conformers i and r of B interacting with their receptor counterparts, then the fractional response is directly proportional to the fraction of bound sites y, possessing the initiating response, the sites being defined by BiRjx. Applying simple Gaddum theory [3]
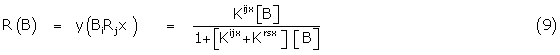
and since the gross binding constant KB is given by
KB = Kijx + Krsx (10)
(9) may be written
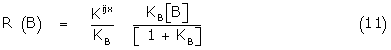
Comparing (8) and (11) gives the simple relations
Kijx = eKB
Krsx = (1-e) KB (12)
It follows from (11) that a plot of R(B)/eB /(1-R(B))/eB against [B] in a Hill plot yields KB, while simple use of the efficacy in (12) yields the conformer binding constants. The position is summarized in the dose-response relation in Figure 1.
In the case of competitive antagonism of an agonist A by the partial agonist B, it has been shown that a true binding constant KB may be obtained if the dose-response curves are suitably normalised [24].
The total fractional response R (A + B) due to A and B is given by
R (A + B) = eA y(A/B) + eBy(B/A) (13)
where y(A/B) is the mole fraction of A occupying receptors in the presence of B. Using Gaddum theory, the respective mole fractions may be written in terms of the binding constants, so that (13) becomes
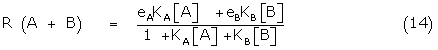
The fractional response of B alone, R(0,B) is given by
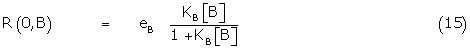
Using (15), the right hand term of 14 can be written
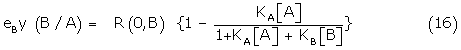
= R (0,B) {1 –y(A/B)} (17)
Substituting (17) in (13) and rearranging
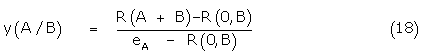
Plotting of the data in the form (18) allows a true comparison of the dose shift in the agonist A response due to the presence of B and from the Schild plot an exact KB is obtained. The dose-response relation is summarized in Figure 2. Again, eB may be defined as Kijx / KB allowing the conformer binding constants to be determined.
Figure 2: Dose-response curves for competitive antagonism of a full agonist A by a partial agonist B for given doses of B. For the given dose of the latter, the combined response of A and B, R(A+B), is shown relative to the response of B alone, R(0,B). The scaling factor eA – R(0,B) is also indicated which, for the maximum response of B, may be written eA (1 - eB/eA).
Signal amplification and response as a hyperbolic function of receptor occupancy: It will be shown that the form of the relationships are very similar to the linear model when the amplifying functions for full and partial agonists are competitive in nature but only apparent binding constants KA/ and KB/ can be determined. Discriminating between agonist and antagonist conformers on the other hand shows that the antagonist conformer component of the binding Krsx represented by (1-eB) KB/ is an exact component of the binding.
For the general Black and Leff model of signal amplification. The fractional response R(B) of the partial agonist B is some hyperbolic function z of the bound receptor complexes BiRjx initiating the response
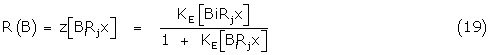
where Ke is the effective binding constant of the subsequent amplifying function and from (9) and (10)

Writing the bound fraction in terms of the concentration of the total receptors, RT and combining (19) and (20)
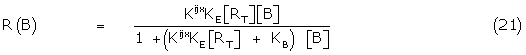

Where 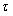 = KE [RT ], and KB/ = KB + Kijx
= KE [RT ], and KB/ = KB + Kijx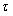 = Krsx + Kijx (
= Krsx + Kijx (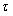 + 1).
+ 1).
(21) may also be written
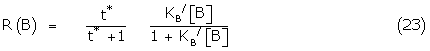
where 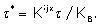
Equation (22) is the exact form of the Black and Leff model but the amplification factor is modified by the drug mechanism factor Kijx / KB.
The fractional maximum response, eB, is explicitly represented as 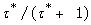
For the agonist response, the plotting of R(B)/eB / (1 - R(B)/eB) against [B] in a Hill plot now yields the EC50 value as 1/KB/ where the true binding constant contains an additional term Kijx  from the signal amplification of the agonist binding. It will prove convenient to use the term, apparent binding constant so defined.
from the signal amplification of the agonist binding. It will prove convenient to use the term, apparent binding constant so defined.
Since the fractional maximal response may be represented in the form

It might appear that true binding constants could be obtained by scaling the observed KB/ by (1– eB). However, it is implicit in the hyperbolic model that the observed fractional efficacy eB is measured as eB/eA, where eA, the maximum fractional response of the full agonist, A, is  /(
/( + 1) (strictly an extrathermodynamic property in relation to the partial agonist).
+ 1) (strictly an extrathermodynamic property in relation to the partial agonist).
For the observed parameter, therefore,
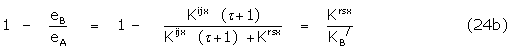
The binding constant of the dominant antagonist conformer is thus obtained from such scaling. The dose-response relation is summarised in Figure 3. It may be noted that the  factor governing the signal amplification may be large as with a full agonist but the binding constant of the agonist Kijx would then be relatively small. In the event of different amplifying functions,
factor governing the signal amplification may be large as with a full agonist but the binding constant of the agonist Kijx would then be relatively small. In the event of different amplifying functions, 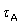 and
and 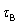 regulating the responses of A and B, relation (24) becomes
regulating the responses of A and B, relation (24) becomes
Figure 3: Response as a hyperbolic function of receptor occupancy. Doseresponse curves for a full (A) and partial (B) agonist showing proportionality relations between the conformer binding constants (agonist, Kijx ; antagonist, Krsx), and the amplification component, Kijxτ as a function of the maximum stimulatory response, eB. The signal amplification factor τ is, here, assumed common for both full and partial agonist responses.
The wider the difference in signal amplification of B in relation to the agonist A, the closer its effective antagonist conformer binding constant will approach the true binding constant.
The competitive challenge of an agonist A by a partial agonist B may now be considered. The separate signal amplifying functions, 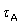 and
and 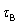 , are retained for generality. These amplification factors may be independent but in the case of bound conformer complexes competing for a given amplifying system E , competitive interaction will arise. We confine ourselves, here, to this constrained condition. The unconstrained conditions may be developed but some approximation is required for solution and is discussed briefly in Section 3. The bound agonist conformer A is written for completeness as Kabx where a and b are the respective ligand- receptor bound conformers
, are retained for generality. These amplification factors may be independent but in the case of bound conformer complexes competing for a given amplifying system E , competitive interaction will arise. We confine ourselves, here, to this constrained condition. The unconstrained conditions may be developed but some approximation is required for solution and is discussed briefly in Section 3. The bound agonist conformer A is written for completeness as Kabx where a and b are the respective ligand- receptor bound conformers
The fractional response of A alone may be written as the equivalent of (21)

Where Kabx  A + KA = KA/ , the apparent binding constant of A.
A + KA = KA/ , the apparent binding constant of A.
By comparison with (9) and using Gaddum theory [3], the fraction of bound complex AaRbx / B in the presence of B, y(AaRbx / B) is given by
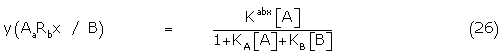
and a similar expression for y(BiRjx / A) exists with the numerator Kijx[B]. The relevant interactions of the bound complexes competing for the amplifying system E may be written

with the appropriate binding constants KEA and KEB respectively.
Again using simple Gaddum theory, the fractional response of A in the presence of B, R(A/B) is giben by the fraction y of AaRbxE complexes present
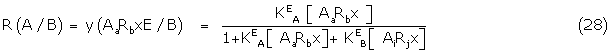
and similarly
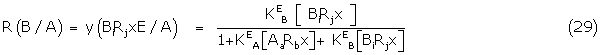
Substituting the appropriate concentrations of Aa Rbx and BiRjx from (26) and its counterpart
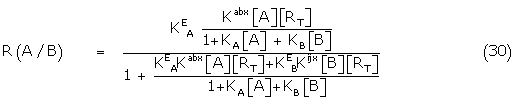
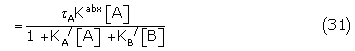
where 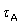 = KEA[RT], eA =
= KEA[RT], eA = 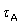 Kabx /KA / and KA/ and KB/ are the apparent binding constants.
Kabx /KA / and KA/ and KB/ are the apparent binding constants.
Similarly, the response of B in the presence of A is given by

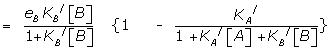

where R(0,B) is the fractional response of B alone.
Since R(A+B) = R(A/B) + R(B/A) and using (34)

Equation (35) is simply the Ferguson-Robertson relation but the Langmuir representation contains apparent as opposed to true binding constants. Plotting of the data against the equivalent response of A alone thus gives the classical dose-shift of 1 + KB/ [B] on the log concentration scale. The same arguments obviously apply for the condition 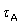 =
= 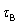 . Again, the antagonist conformer binding constant should be readily obtained using (24).
. Again, the antagonist conformer binding constant should be readily obtained using (24).
The generalised BLACK and LEFT hyperbolic relation and associated models
When the generation of a second messenger is produced by an activated complex leading to a sequence of events to produce a final hyperbolic response then a series of related hyperbolic models must exist with appropriate 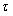 ‘s. If a common second messenger arises from the two bound activated complexes produced by an agonist A competing with a partial agonist B, then the constrained model for signal amplification is the most appropriate for any subsequent amplifying process. The question arises as to whether conformer binding constants of a partial agonist are obtained from the doseresponse relation in a more general Black and Leff hyperbolic model.
‘s. If a common second messenger arises from the two bound activated complexes produced by an agonist A competing with a partial agonist B, then the constrained model for signal amplification is the most appropriate for any subsequent amplifying process. The question arises as to whether conformer binding constants of a partial agonist are obtained from the doseresponse relation in a more general Black and Leff hyperbolic model.
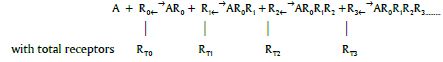
the response function may be written
R (AR0R1R2.....RN) = L( N L(
N L( N-1.....L(T1 L(K0[A])....)
N-1.....L(T1 L(K0[A])....)
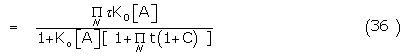
Where the hyperbolic Langmuir function L(x) = x/(1 + x)
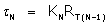
And 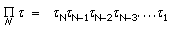
The constant C contains all lesser products of  ‘s and is approximately
‘s and is approximately 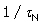 if all
if all 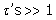 . The response may also be written
. The response may also be written
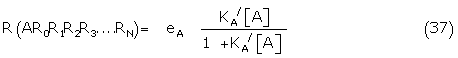
where 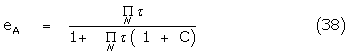
It might appear, therefore, that unless the contribution of C were negligible, only approximate estimates of K0 could be obtained by scaling the apparent binding constant by ( 1-e). However, relative scaling of the partial agonist by the full agonist automatically takes care of such factors if the signal response has a common amplification. Thus for the conformer model of the partial agonist B,
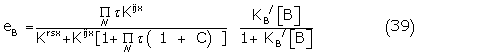
where 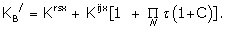
Using (38) as the conformer representation for the full agonist with 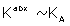
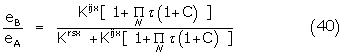
and

Finally it may be noted that in the presence of competitive mechanisms due to the presence of a set of endogenous species Xi, the constrained model for signal amplification will still produce the correct binding constant provided that the endogenous materials remain constant through the time course of the experiment.
This was first shown by Robertson [24].
Equation (32) may be written
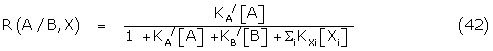
where R(a/B,X) is the response of A in the presence of B and the species X.
It is straightforward to show that
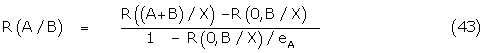
The Ferguson–Robertson relation is again obtained and plotting of the data against the equivalent response of A in the presence of X gives the classical dose shift of 1 + KB/ [B].
The unconstrained model for signal amplification is briefly considered where the conformer-receptor complexes have noncompetitive amplifying systems associated with the receptors. Such a case for dose – response theory appears unlikely but is commented on for completeness. It may be shown that R(B/A), the response of B in the presence of A, can be written
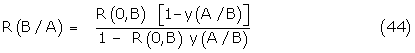
but leads to second order terms in the fraction y(A/B) when finding the expression for the total response R(A + B).
Early evidence that partial agonists give identical binding constants determined from agonist and antagonist responses may be cited [8] indicating that the constrained model for signal amplification is the pertinent model.
β1 and β2 –adrenoceptor function in cardiac tissue
A tissue response dominated by a single receptor where ligands are closely related to the natural hormone is likely to provide the most direct insight into energetic differences in hormonal binding. Early work [25,26] indicated that the guinea pig right atrial chronotropic and left atrial inotropic responses were dominated by the β1- adrenergic receptor. The determination of pA2 values for selective antagonists (atenolol - β1; α-methyl propranolol - β2 ) with the use of selective agonists (fenoterol - β2-; noradrenaline - β1), showed that the values did not vary with the agonist in contrast to data on cat atria and guinea pig trachea, indicating the dominance of a single receptor. A more selective β2- antagonist, ICI 118,551 giving more than 50-fold selectivity on the tracheal response using fenoterol again may be compared with equipotent results on the guinea-pig atria using the β1- or β2- selective agonist [27].
An even more highly selective potent β2-adrenoceptor agonist, T-2005 (β1/β2 ratio 256 [28]) showed that the inotropic response in guinea pig right and left atria and papillary muscle were mediated by the β1-adrenoceptor only. However, for the right atrial chronotropic response, the compound exerted a biphasic response, the first phase being mediated by β2-adrenoceptors and the second phase by β1-adrenoceptors approximately 64% of the overall chronotropic response being exerted by the β2-receptor giving a 50% response compared with isoprenaline. In moving from 50 to 250-fold β2/β1 selectivity, therefore, preferential activation of β2-receptors in the chronotropic response is possible.
Displacement studies given in this paper [28] indicate a 6:1 ratio of β1 /β2 receptors in the guinea-pig right atrium indicating a signal amplification factor of approximately 3 in TA-2005 to attain a 50% maximum response. The signal amplification,  1 for the β1-response appears less than this value with a long linear response in the last 50-90% of T-2005’s concentration-response curve. On the other hand, the signal amplification factor for the β-agonist, isoprenaline determined by progressive elimination of the receptor pool of β-receptors in guinea-pig right atria showed signal amplification factors of 10-30-fold [29-31] determined independently and in this laboratory while a similar 20-30 fold amplification factor was shown for the rat left atrium [32-34]. For non-selective binding of a ligand to two receptors with conserved residues, in the effective receptor sites, a Langmuir hyperbolic concentration-response curve will only be obtained if the ligand binding is effectively identical in the two conserved receptor sites but the signal amplification may vary, giving proportional fractional contributions to the resultant signal response. The more than 50-fold selective β2--antagonist, ICI 118,551 shows no significant β2-signal influence on the guinea–pig right atrial chronotropic response, the guinea-pig trachea showing a 44-fold increase in potency when the β2-agonist, fenoterol was used compared with adrenaline, the atrial response giving identical values. The Langmuir plots of fractional response against log10 molar concentration of isoprenaline and prenalterol for increases in rate of individual guinea-pig right atria are later shown in Figure 4 where linear unit slopes are accurately maintained for both compounds over the range of the concentration-response curves. Taken overall, the data can be consistent with a 15-20 fold amplification of 6/7 of the signal being through β1- and a 3-fold amplification through 1/7 of the stimulus through β2-receptors giving a more than 95% dominance of the β1-response under normal signalling conditions.
1 for the β1-response appears less than this value with a long linear response in the last 50-90% of T-2005’s concentration-response curve. On the other hand, the signal amplification factor for the β-agonist, isoprenaline determined by progressive elimination of the receptor pool of β-receptors in guinea-pig right atria showed signal amplification factors of 10-30-fold [29-31] determined independently and in this laboratory while a similar 20-30 fold amplification factor was shown for the rat left atrium [32-34]. For non-selective binding of a ligand to two receptors with conserved residues, in the effective receptor sites, a Langmuir hyperbolic concentration-response curve will only be obtained if the ligand binding is effectively identical in the two conserved receptor sites but the signal amplification may vary, giving proportional fractional contributions to the resultant signal response. The more than 50-fold selective β2--antagonist, ICI 118,551 shows no significant β2-signal influence on the guinea–pig right atrial chronotropic response, the guinea-pig trachea showing a 44-fold increase in potency when the β2-agonist, fenoterol was used compared with adrenaline, the atrial response giving identical values. The Langmuir plots of fractional response against log10 molar concentration of isoprenaline and prenalterol for increases in rate of individual guinea-pig right atria are later shown in Figure 4 where linear unit slopes are accurately maintained for both compounds over the range of the concentration-response curves. Taken overall, the data can be consistent with a 15-20 fold amplification of 6/7 of the signal being through β1- and a 3-fold amplification through 1/7 of the stimulus through β2-receptors giving a more than 95% dominance of the β1-response under normal signalling conditions.
Agonist and Antagonist Conformer Binding Constants for Prenalterol on the β1- Adrenergic Receptor at 30.0°C.
Guinea - pig isolated right atria
Guinea pigs (male, Dunkin Hartley, 250-450mg) were killed by a blow to the head and exsanguinated under running water. The thorax was rapidly opened and the spontaneously beating right atrium was removed. Cotton loops through the inferior cava and the atrioventricular junction attached it to the tissue holder. A third cotton through the superior vena cava connected the atrium to an isometric force transducer (Devices, UF1, 57g sensitivity range). The atria were immersed in a 50ml organ bath containin Krebsbicarbonate solution. In double distilled water of composition (nm NaCL 118.4, KCl 4.7, CaCl2.2H2O 1.9, NaHCO3 25.0, MgSO4.7H2O 1.2, D-glucose 11.7, NaH2PO4.2H2O 1.2 . The tissues were gassed with 5% CO2 in oxygen at 30.0 ± 0.3°C).
Isometric tension was recorded on a Devices M19 polygraph (Lectromed, Welwyn Garden City). Initial resting diastolic tensions of 0.5-0.8 g were applied to the atria. Spontaneous rate of contraction was recorded from the tension signal by means of a rate meter (Devices, type 2751).
Experimental protocol
Tissues were allowed to equilibrate for 1h, with changes of bathing medium before (±)-metanephrine was added to the bath (10µM) to inhibit extraneuronal uptake and which was present throughout for the remainder of the experiment. After a further 30 min, a concentration-response curve for (-) isoprenaline was constructed by cumulative addition in half logarithmic increments until the maximum was achieved. The tissue was then washed every ten minutes until the original atrial rate of contraction was achieved (approximately 40 minutes) before obtaining a second curve for the prenalterol. The restoration of resting rate ensured that no residual isoprenaline was present. The concentration of prenalterol producing the maximum increase in rate (8.39 x 10-6 M) was left in contact with the atria for 30 minutes before commencing a second curve for isoprenaline in its presence. Time-matched control experiments were performed in which the atria were exposed to two consecutive concentration-response curves for isoprenaline but without the intervening exposure to prenalterol.
Measurement and plotting of responses
Increases in rate of contraction in individual experiments were obtained by subtracting the respective pre-curve resting rate from the total developed rate at each concentration of isoprenaline or prenalterol. The increases in rate were then plotted as a percentage of the initial maximum increase (eA), the maximum response to prenalterol being eB (Figure 1).
The EC50 values for isoprenaline were obtained from these curves as the molar concentration for a 50% response by linear fitting of the data to the Langmuir relation utilising points generally over the (20-80)% range of response. The EC50 values for prenalterol were obtained similarly after replotting the increases in rate as a percentage of their own maximum.
For the antagonist effect of prenalterol, the increases in rate for isoprenaline above the prenalterol response are R(A+B) –R(0,B) (where in these experiments R(0,B) = eB, the maximum response). These were expressed as a percentage of the maximum increase obtained in the presence of prenalterol (eA-eB) (Figure 2). The shift of the isoprenaline curve was expressed as the dose-ratio of the EC50 values before and after prenalterol. In control experiments, the increases in rate in response to isoprenaline were expressed as a percentage of the respective maximum increase. The EC50 values were calculated for the first and second curves by linear fitting of the data to the Langmuir relation utilising points over the (20-80)% range of response. The slopes of the 1st curves of control experiments at 40.0 and 25.0°C were not significantly different from unity, although at 30.0°C there was a significant deviation (0.83 ± 0.03 refer Table 1). At all temperatures no significant change in the slope was observed between 1st and 2nd curve of control experiments. The change in sensitivity between 1st and 2nd curve was, therefore, expressed as the dose-ratio of the EC50 values. The EC50 values of 1st and 2nd curves were not significantly different indicating that there was no desnsitization of β1-adrenocep[tors between 1st and 2nd exposures. The EC50 value for the initial isoprenaline curve of the test experiments was corrected by dividing by the correction factor before estimating the dose-ratio for the shift in the isoprenaline curve by prenalterol, to bring the responses to near time-equivalence.
| Temperature (°C) | 40.0 | 37.5 | 30.0 | 25.0 |
| No. of experiments | 7 | 8 | 6 | 8 |
| Slope of 1st Isoprenaline Curve | 0.92 ± 0.06 | 1.02 ± 0.03 | 0.83 ± 0.03 | 0.95 ± 0.04 |
| Slope of 2nd Isoprenaline Curve | 0.82 ± 0.03 | 1.03 ± 0.05 | 0.81 ± 0.03 | 1.02 ± 0.08 |
 |
0.17 ± 0.03 | 0.095 ± 0.04 | 0.06 ± 0.05 | 0.02 ± 0.06 |
Table 1: Mean Slopes of Linear Fitting for the Hyperbolic Langmuir Model to 1st and 2nd Isoprenaline Dose-Response Curves and Mean Corrections for Changes in EC50 between the two Curves.
Apparent binding constants for prenalterol, KB/
The binding constants for prenalterol were determined from 1) the agonist response using the EC50 values and 2) the antagonist response using the Ferguson-Robertson method. The agonist conformer binding constant, Kijx ( + 1) with its associated amplification factor
+ 1) with its associated amplification factor  and the antagonist conformer binding constant, Krsx were determined from the simple relations as given in (24 ) as reported earlier [35].
and the antagonist conformer binding constant, Krsx were determined from the simple relations as given in (24 ) as reported earlier [35].
eB KB/ = Kijx ( + 1)
+ 1)
(1- eB) KB / = Krsx(45)
The derived conformer binding constants were also compared with the binding constant determined by the method of Waud [39]. This method, dependent on the comparison of equivalent responses by tbe full agonist A and the partial agonist B, yield the antagonist conformer binding constant Krsx directly, the slope/intercept of the reciprocal plot of 1/A against 1/B in (46) giving 1/[KB/(1 – eB/eA)].
Evaluation details are briefly given. Corrections for the dependence of the first isoprenaline curves were made only for the Ferguson-Robertson method. The correction to the isoprenaline curve in the Waud method cancels in the slope/intercept relation and was not applied. In this method, equieffective concentrations of the full (A) and partial (B) agonist were measured above 20% of maximum isoprenaline response, while the reciprocal plot of [1/A] against [1/B] was weighted using the method of Kaumann [41].
Drugs used (-) Isoprenaline bitartrate dehydrate (Sigma) and (±)– metanephrine hydrochloride (Sigma) were obtained commercially and prenalterol hydrochloride (H 133/22, (-)-1-(4-hydroxyphenoxy)-3- isopropyl-1-amino--propan-2-ol) (A B Hassle, Goteborg, Sweden) was generously provided as a gift.
Table 2 shows the prenalterol apparent binding constants, KB/ on the log10 scale, determined from the agonist response (EC50) and the antagonist response (Ferguson–Robertson [F-R]) at 30.0°C on the guinea-pig cardiac β1-adrenergic receptor. Only experiments in which both isoprenaline and prenalterol obeyed the hyperbolic Langmuir form were accepted. Six of the eight EC50 experiments obeyed this criterion and are shown within the central intermittent lines. Mean values are given for all eight as well as selected data and the number of experiments bracketed for each methodology. Little variation is shown by omitting extrema points based on the criteria of efficacy and Langmuir slope. Plots of Response/1-Response against concentration both on the log10 scale are shown for isoprenaline and prenalterol in Figure 4. In addition to the data at 30.0°C over 70% of all test experiments carried out between 25.0°C and 40.0°C were accepted using this criterion.
No significant difference between the mean log10 KB/ values was detected (7.39 ± 0.07 (6), (EC50); 7.43 ± 0.10 (4), (F-R)), indicating, as expected, the constrained model for signal amplification, that is to say, competitive occupancy of the receptor site by agonist and partial agonist must exist for any signal amplification. Prenalterol displayed the expected partial agonist activity with a mean maximum rate of increase of 0.558 ± 0.035 (8) (Table 2 and Figure 5). A slightly larger sample determining only the maximum response gave a slightly lower value while omitting the extrema points gave 0.546 ± 0.01. Using the latter value of efficacy, the method of Waud for determining the binding constant which, as shown above, determines only the antagonist form, Krsx is expected to give a value for log10 KB/ of 7.19 ± 0.07. The difference in the corrected Waud estimate for log10 KB/ is now not significant from the two determinations cited above although the methodology using double reciprocal plots and reliant on a slope/ intercept relation to establish the Krsx value is likely to be subject to limits in accuracy. Figure 5B shows the double reciprocal plot for equieffective concentrations of isoprenaline and prenalterol obtained from the mean curves which were utilised in this method.
Figure 5: A. The Waud method. Mean (n=5) concentration-response curve for the increases in rate of guinea-pig atria to isoprenaline () and prenalterol ( (۞ plotted as a percentage of the isoprenaline maximum. B. Double reciprocal plots of equieffective concentrations of isoprenaline (1/A) and prenalterol (1/P) obtained from the mean plot in A.
| Efficacy eB/eA | EC50 measurements | Ferguson-Robertson | Waud log10 Krsˆ | ||||||
| Log10 BK⁄ | Log10 Krsˆ | Log10Kij′(τ + 1) | Langmuir Slope | Log10 BK⁄ | Log10Krsˆ | Log10Kij′(τ + 1) | Langmuir * Slope | ||
| 0A2 | 7.24 | 7.00 | 6.86 | 1.14±0.05(3) | 7.58 | 7.34 | 7.20 | 0.92±0.04(4) | 6.950.03 |
| 0.51 * | 7.27 | 6.97 | 6.98 | 1.03±0.06(4) | - | - | - | - | - |
| 0.52 | 7.37 | 7.05 | 7.09 | 1.00±0.08(4) | 7.29 | 6.97 | 7.00 | 1.005±0.05(3) | 6.82±0.07 |
| 0.54 * | 7.19 | 6.86 | 6.92 | 0.85±0.02(4) | - | - | - | - | - |
| 0.56 | 7.71 | 7.35 | 7.46 | 0.86±0.10(4) | 7.25 | 6.89 | 7.00 | 1.00±0.08(4) | 7.05±0.07 |
| 0.565 | 7.A1 | 7.05 | 7.16 | 0.990.07(4) | 7.48 | 7.12 | 7.23 | 0.91±0.06(6) | 6.71±0.04 |
| 0.58 | 7.A1 | 7.03 | 7.17 | 1.04±0.04(4) | 7.70 | 7.32 | 7.46 | 0.75±0.00(3) | 6.84±0.04 |
| 0.77 | 7.86 | 7.22 | 7.74 | 1.68±0.02(3) | 7.70 | 7.06 | 7.59 | 1.30±0.10(3) | - |
| Means ± SEM 0.558 ± 0.035 7.432 ± 0.083 7.066 ± 0.054 7.17 ± 0.10(8) 7.500 ± 0.080 7.117 ± 0.074 7.247 ± 0.098(6) 0.546 ± 0.011ˆ 7.393 ± 0.072 7.060 ± 0.061 7.130 ± 0.077(6) 7.430 ± 0.10 7.075 ± 0.094 7.17 ± 0.11(4) 0.93 ± 0.07(4) 6.855 ± 0.071(4) |
|||||||||
° EC50 data only available
* Slope of Langmuir relation for R (A/B).
Comparative means for the efficacies of the Ferguson-Robertson results are 1) 0.569+0.047 (6) 2) 0.556+0.012(4).
ˆ Omitting extreme points on efficacy
Table 2: Apparent binding Constants ( BK/ ), Efficacies (eB/eA), Antagonist (Krsˆ) and Agonist (Kij'(τ + 1)) Binding Components of Prenalterol at 30.0°C on the Guniea pig Cardiac β1 –Adrenoceptor.
The Ferguson-Robertson method which yields a true dose shift of log10 (1+ KB/[B]) over the range of concentration of the agonist is shown in Figure 6, The concentration-response curve for isoprenaline in the presence of prenalterol established upon the maximum induced rate achievable by prenalterol.is shown in Figure 6A The maximal induced rate achieved by isoprenaline (198.2 ± 3.5 beats min-1 ) was not significantly different from the pre-prenalterol maximum (200.3 ± 4.5 beats min-1). The normalised Ferguson-Robertson curve for isoprenaline in the presence of prenalterol is shown in Figure 6B.
Figure 6: The Ferguson-Robertson Method. Mean (n=6) concentrationresponse curves on guinea-pig atria for isoprenaline in the absence () and presence (♦) of a maximum concentration (9 x 10-6M) of prenalterol. The increases in rate in the presence of prenalterol, R(A+B), are measured either above the prenalterol-induced rate eB or above the maximum pre-prenalterol resting rate (eA - eB) (Fig. A) and expressed as a percentage of the maximum. The dose shift for equieffective responses now gives the classical dose-shift 1 + KB / [B] (Fig. B).
The driving force for an alternative description of the characteristic ligand parameters of binding and efficacy into two molecular determinants lies in the very different thermodynamics of binding of particular agonists and antagonists observed on the β1-adrenergic receptor which encompass specific small molecular changes. The recognition by Black and Leff that a single effective amplifying parameter is all that is required to describe an agonist obeying a hyperbolic dose-response relationship implies that within a partial agonist it should be possible to separate the binding into agonist and antagonist components where the amplification factor,  , is obviously associated only with the agonist component. A comparison of parameters obtained from the Black and Leff model with its simple extension here to embrace the two types of complex is given in Table 3 where a common amplifying function is assumed to affect both full and partial agonist. In the Black and Leff model,
, is obviously associated only with the agonist component. A comparison of parameters obtained from the Black and Leff model with its simple extension here to embrace the two types of complex is given in Table 3 where a common amplifying function is assumed to affect both full and partial agonist. In the Black and Leff model,  is simply an operational model of the efficacy. In the current model separating agonist and antagonist complexes,
is simply an operational model of the efficacy. In the current model separating agonist and antagonist complexes,  may be a constant but relative efficacies are dependent on the drug receptor binding of the agonist conformer with its associated binding constant, Kijx even where the dominant mode of binding of the antagonist conformer to the receptor may be constant (Krsx constant) and the amplifying process is a common one, a condition apparently shown by a set of 2-substituted phenoxypropanolamine analogues of prenalterol [19].
may be a constant but relative efficacies are dependent on the drug receptor binding of the agonist conformer with its associated binding constant, Kijx even where the dominant mode of binding of the antagonist conformer to the receptor may be constant (Krsx constant) and the amplifying process is a common one, a condition apparently shown by a set of 2-substituted phenoxypropanolamine analogues of prenalterol [19].
| Observed Parameter | Black and Leff | Conformer Representation+ |
| K⁄B or KB/ | KB (τ + 1) | Kijx τ + KB* |
| KB/(1–eB/eA) | KB | Krsx |
| KB/(eB/eA) | KBτ | Kijx (τ + 1) |
* when τ = τA = τB
* where KB = Krsx + Kijx
Table 3: Comparison of Parameters for a Partial Agonist using the Black and Leff and Conformer-Receptor Binding Models when a Common Amplifying Process is Assumed Applicable to Full (A) and Partial (B) Agonist Responses.
From a chemical viewpoint, the efficacy (e) appears a rather neglected parameter in pharmacology, the ratio e / (1 – e) on the thermodynamic scale representing the difference in the free energies of ligand binding between agonist and antagonist complexes given the adapted Black and Leff model. To determine the enthalpy difference in binding between these two complexes to an accuracy of 1.0 -1.5 kcal/mol over a 15°C range of temperature, the measure of efficacy should be to within ±0.025 log10 units and the data are of this order. The enthalpy associated with  , if present, is then an additive component in the binding enthalpy observed for the ligand agonist conformer. If the binding differences lie within one given conformer (in the particular case expected here [19]), this enthalpy change is one of particular simplicity. Self consistency in binding constants determined from the EC50 and from antagonism using the Ferguson-Robertson method implies constraints on the form of of the signal amplification in the Black and Leff model. As expected this is shown by prenalterol, binding to the guinea-pig cardiac β1- adrenergic receptor where the conformer-receptor complexes must compete for the amplifying system or a common second messenger arising from the two bound conformers develops a subsequent amplifying response. This constrained model for signal amplification is concordant with the production of the second messenger cyclic AMP in the cardiac β1-adrenoceptor adenylyl cyclase system. Direct evidence for the absence of amplification in the production of cyclic AMP has been reported [35]. Over the range of response evaluated, the data do not support a two state receptor [37] or mobile-receptor [13] cooperative model. Membrane-binding studies in the absence of GTP do, however, support such models [37]. These observations are in agreement with the view that the β1-adrenergic receptor-G protein adenyl cyclase system is integrally held within the membrane, or that each event proceeding from the agonist-receptor interaction may be treated in relative isolation without amplification before the release of the cyclic AMP.
, if present, is then an additive component in the binding enthalpy observed for the ligand agonist conformer. If the binding differences lie within one given conformer (in the particular case expected here [19]), this enthalpy change is one of particular simplicity. Self consistency in binding constants determined from the EC50 and from antagonism using the Ferguson-Robertson method implies constraints on the form of of the signal amplification in the Black and Leff model. As expected this is shown by prenalterol, binding to the guinea-pig cardiac β1- adrenergic receptor where the conformer-receptor complexes must compete for the amplifying system or a common second messenger arising from the two bound conformers develops a subsequent amplifying response. This constrained model for signal amplification is concordant with the production of the second messenger cyclic AMP in the cardiac β1-adrenoceptor adenylyl cyclase system. Direct evidence for the absence of amplification in the production of cyclic AMP has been reported [35]. Over the range of response evaluated, the data do not support a two state receptor [37] or mobile-receptor [13] cooperative model. Membrane-binding studies in the absence of GTP do, however, support such models [37]. These observations are in agreement with the view that the β1-adrenergic receptor-G protein adenyl cyclase system is integrally held within the membrane, or that each event proceeding from the agonist-receptor interaction may be treated in relative isolation without amplification before the release of the cyclic AMP.
For the constrained model of signal amplification, all pharmacological methods for determining the binding constant of a partial agonist should show self sufficiency and differ only in the accuracy of the experimental procedure. Both the methods of Waud [39] and Ruffolo [40] using equieffective concentrations of full and partial agonists do not yield a true KB/ but (1-eB/eA)KB/, the antagonist binding constant, Krsx .Stephenson [6] and Kaumann [41] who examined full agonist responses in the absence and presence of the partial agonist assume that the full agonist is linear in behaviour neglecting the normalisation factor of (1 + KA/ [A]) in denominator terms on the basis that [A] is always small but, again, neglect the response amplification factor inherent in the full agonist. The Ferguson-Robertson method demonstrates that there is no requirement for approximation. If temperature studies are to be performed to discriminate between the binding thermodynamics of agonist and antagonist complexes, it is important that an exact representation of the apparent binding constant is given. The current representation is, of course, dependent on the Black and Leff operational model of agonism, the only requirement of which is that the dose-response relation is of hyperbolic form and itself dependent on single receptor site occupancy by the ligand.
While clearly the most appropriate method for evaluating the gross binding constant, KB, may depend on the degree of partial agonist activity, both the EC50 and Ferguson-Robertson methods employ the full range of the dose-response curve and are concluded to be the preferred methods for accurate determinations of the apparent binding constants. Comparative values of the agonist component, eB/eA KB/, should, therefore, yield accurate comparative differences of conformer binding constants for a common system of amplification.
Approximations to the apparent binding constant are expected not to vary by more than 0.3 log10 units as discussed above. Similarities between the dissociation constants (pKp values) for prenalterol at 34.0°C in the guinea pig left atria determined by the Waud (7.5 ± 0.18), Stephenson (7.4 ± 0.2) and van Rossum (7.3 ± 0.16) methods have been earlier pointed out by Kenakin and Beek [42]. Studies with other β-adrenoceptor antagonists having intrinsic sympathomimetic activity show the expected small difference between the EC50 determination of the apparent binding constant, KB/, and determination of the antagonist contribution KB/(1-eB/eA) (Kaumann and Blinks [43]) The differences are of the correct order for the conformer representation.
In the case of any larger discrepancy due to the delayed onset of the agonist response as reported by these latter authors, a possible model is given by (47)
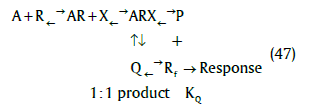
where a second equilibrium affecting the formation of the response may occur and a further hyperbolic function in terms of Q will affect the response but evidence for such a model is required.
Wide reviews of thermodynamic measurement of ligand-receptor binding have been made giving general profiles and their possible influence on binding and efficacy [44,45]. In contrast, we have limited consideration to examining the requiremnts and methodology for understanding partial agonism by a close comparison of two ligands with a response ‘in vitro’ very dominated by a single receptor under normal signalling conditions.
The position on transposing the two pharmacological parameters of binding and efficacy into two binding components related to agonist and antagonist conformer complexes may be summarised.
1. If the signal from bound agonist-receptor conformer complexes is amplified, then self-consistency of apparent binding constants, KB/, determined from the EC50 agonist response or from the antagonist response using the Ferguson-Robertson method implies constraints on the mode of amplification. Using an adapted Black and Leff model, a common process of signal amplification must exist for full and partial agonists. The Black and Leff amplifying factor,  is effectively constant for a given receptor in a given tissue.
is effectively constant for a given receptor in a given tissue.
2. The conformer binding constants are simply related to the efficacy, the term (1 – eB/eA) KB/ where eA and eB are the maximum stimulatory responses of the full and partial agonist, define the antagonist binding constant, Krsx where r and sx are the respective interacting conformers of drug and receptor. This conformer component is determined directly by a number of pharmacological methods. The proportional efficacy term, eB/eA KB/ defines the agonist conformer component Kijx ( +1) which is always coupled to its amplification factor,
+1) which is always coupled to its amplification factor,  .
.
3. Differences in the free energy of binding of the respective agonist and antagonist complexes is dependent only on the efficacy ratio eB/eA/(1 – eB/eA). Temperature studies on the efficacy alone, yield the enthalpic differences between the two complexes.
4. The constrained model of signal amplification is applicable to the action of the phenoxypropanolamine, partial agonist, prenalterol, on the guinea pig cardiac β1-adrenergic receptor at 30.0°C.
The authors would like to thank the late Sir James Black, Nigel Shankley and H.H.Robertson for their careful reading of the early manuscript of this paper and acknowledge the latter’s original development of the Ferguson-Robertson method. The authors also acknowledge the support given to the work by ICI under the SERC CASE award No. BC/117 (1985).