Advanced Techniques in Biology & Medicine
Open Access
ISSN: 2379-1764
ISSN: 2379-1764
Short Communication - (2013) Volume 1, Issue 1
The clinical and analytical specificity and sensitivity are dependent on the advancement of laboratory tools. Hereupon, one of the main aims of new laboratory equipments is to develop the Limitations of Detection (LOD) of trace markers. Although the routine use of low LOD markers may be critical in clinical diagnoses but, the quality control parameters should be managed during their measurements. It is obvious that the data assurances are associated to tools, methods and materials, but a simple concept must be followed for data quality analysis in clinical laboratories. Here, some IQC parameters are mentioned to be applied and evaluated by staffs in clinical laboratories.
The standard curves may be prepared on the basis of line or scatter modes (Figure 1). The line mode is suggested when the standard points are not correlated or the changes of the different standard concentrations are not fitted on the regression curve. In this mode, near standard points may be independently associated on the line. In scatter mode, the distances of standard points from the fitted line are at the allowable range so that the best standard equation is plotted on the boot-strapping technique and the Root-Mean-Square Error (RMSE).
Figure 1: Standard curves with Line ■ and scatter ■ modes. In the above plot, the standard points 6-10 are placed between 15000 and 16300 and between 13200 and 17100 in the line and scatter modes, respectively. The bottom plot shows the predicted errors • for standard points on the logarithmic equation (y=151.78+7380.76*ln(x), best RMSE).
With the consideration of significant benefits of quality management in improvement of industry products [1], the qualitycontrol definitions and terms were used in the clinical laboratory fields [2]. However, the approaches of managing were different in two fields based on the material characteristics and sample repeatability. While the primary materials in the industry products are almost the same but, the laboratory sample matrices are different on individual variations [3]. Moreover, the use of pooled sample and calibrator insTEαd of the patient sample is due to the limitations on the laboratory repeatability [4].
The quality-control parameters are most important factors to consider the uncertainty. Several essential questions must be answered before studying this factor. What is the definition of ARL (Average Run Length)? How many calibrators (or pooled samples) should be used in each run (1/Pfr)? How to merge the random and systematic errors? What are the differences of intra-run and inter-run parameters? How to interpret data in each run? My idea is to simplify the IQC measurement conditions by to be concentrated on the basic concepts and reducing of problematic and amazing rules and instructions.
Intra-run quality parameters
In this state, allowable total error (TEα) containing random (Imprecision) and systematic (Inaccuracy) errors (RE and SE) may be used for the decision on the run rejection or acceptance (analytical quality assurance) when their position are identified on OPSPECS Chart [5]. Without consideration of the number of samples in each run, I suggest the use of three calibrators (or pooled samples) to calculate the allowable total error (TEα). The TEα Chart for each laboratory marker can be prepared in the following way:
| RUN | Mean± SD | ValueExp - MeanObs |
| Run1 | MeanObs1± SD1 | ValueExp - MeanObs1 |
| . . . |
. . . |
. . . |
| Run6 | MeanObs6± SD6 | ValueExp - MeanObs6 |
| Total | MeanMeanObs± SD | MeanValueExp - MeanObs |
Three calibrators (cal1+cal2+cal3) are evaluated in each run; Total distribution means should be harmonized; Exp, Expected calibrator value; Obs, Observed calibrator value.





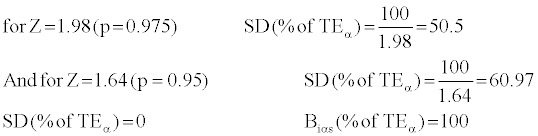
With the use of desirable TEα [6] and the calculation of Bias(%of TEα )and SD(%of TEα ) parameters in each run, and also its identification in the TEα chart, we can make a decision on the run rejection or acceptance. The numbers of total errors in each run are dependent on the linearity and degree of standard curve.
Inter-run quality parameters
One of the main aims to evaluate the between-run variations is to determine the quality of the methods and materials. Levey-Jennings control chart is widely used and developed on Westgard rules [7]. Several factors such as the calibrator (or pooled sample)/sample ratio, the multiple rules must be considered on using the chart.
I suggest the calibrator re-distribution in loop mode (Figure 2) since in the Levey–Jennings control chart, each the calibrator is independently evaluated without the consideration of its role in the data distribution. Although the suggested approach does not show the trends but it omits the primary bias on preparation of rough plot, the redundancy rules and the prediction of the number of calibrators in each run. In this mode, we need only to check the calibrator distributions based on the Z score.
In conclusion, there are two important parameters to evaluate the quality of run data and measuring methods, the TEα and re-distribution charts. The decision on run rejection can be obtained using the TEα chart and, the method accuracy may be evaluated with the calibrator re-distribution in loop mode.