International Journal of Advancements in Technology
Open Access

Towards Sustainable Aluminium Processing: Autonomous Quality Control Using Business Analytics

Kgothatso Matlala^1*, Amit Kumar Mishra¹ and Deepak Puthal^{2 *}Correspondence: Kgothatso Matlala, Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa, Tel: +27-21-460-9333, Email:

Author info »

Introduction

Background on aluminium casting

A typical Aluminium casthouse consists of a sequence of machine centers that performdedicated tasks on the product. Raw, recycled metal is fed into a melting furnace, where itis molten and initial cleaning takes place after large impurities are scraped from the surfaceof the cast. The cast is then transferred to a holding furnace, where it is held further toallow heavy inclusions to sink to the bottom while the lighter ones rise to the surface. Thesurface inclusions are scraped off. The metal is then flown through a launder, where a filter, degasser and metal rod are placed to trap smaller inclusions and other impurities [1,2]. The metal is finally cast into several billets ready for downstream processing. Each billet typically weighs over 10 tons.

Background on aluminium cleanliness measurement systems

To date, several prevalent analytical techniques exist, that are used to characterize metal quality during production. The PoDFA (porous disk filtration apparatus) is a technique for collecting inclusions inside a fine porosity filter disk. The molten Aluminium is extracted from the cast and poured into a heated crucible. Once cooled, the sample is placed under a microscope for metallographic analysis. The PoDFA technique has its strength in its ability to accurately identify inclusions [3,4].

The LiMCA method provides electrical measurements, in which samples are measured every minute. The samples are based on the electrical resistivity of the metal sample, which is directly related to the metal cleanliness [5,6]. A sample of about 30 g is sucked into a tube, where the electrical resistivity of the metal causes a differential in the current produced by two metallic rods. This differential current is directly proportional to the cleanliness of the metal. The LiMCA method has its limitation in the size and frequency of samples that it collects.

The MV20/20 system provides more real-time measurements by measuring 10 samples per second. This is achieved by the usage of ultrasound, where a pulse is transmitted in the metal and the return signal is measured. The MV20/20 measures cleanliness, particle size distributions and a count of inclusions [7,8]. This dataset provides a basis for our study, as it allows for a more comprehensive analysis of metal quality.

Objective

The objective of this study is to implement an autonomous quality control system which realizes real-time measurements, alerts on metal cleanliness anomalies and classifies the inclusion types responsible for the deviation in quality. For this, business analytics, namely descriptive, diagnostic and predictive analytics, is implemented as a proven method for improving business performance. Business analytics is an increasingly important process to how organizations make data-driven decisions. It is a set of processes that involve extracting useful insights from data so as to optimize business performance using an empirical approach. The business analytics process is divided into four components:

Descriptive analytics: This entails analysis of historical data to understand the nature of the business process. Typical outputs are statistical explanations of the data, trend analyses and other descriptive plots.

Diagnostic analytics: This entails analysis of historical data to understand the relationships between events (cause and effect). Typical outputs include correlation plots.

Predictive analytics: This includes the use of historical data to predict future events. Typical outputs include future points with associated mean squared errors for regression, and a confusion matrix for classification.

Prescriptive analytics: This is the determination of the best future scenario based on historical and current trends. Typical outputs include prescriptions of the best configuration of the business process, or specific actions in order to improve current performance or prevent predicted losses. For this work, the applicable components used are descriptive, diagnostic and predictive analytics. The prescriptive analytics component is not applicable as it relies on an existing predictive framework coupled with domain expertise and other available inputs to make relevant prescriptions.

Problem statement

The cast house expressed interest in improving the quality control aspect of the cast house production process. The main problems needing addressing within the scope of this work are:

• P₁-Reduce process waste caused by inclusions, particularly when they cause downstream quality related challenges like metal tearing and customer complaints.

• P₂-Improve time-to-reaction for anomalous situations, when the metal quality is substantially low.

• P₃-Improve the capability for root cause analysis by identifying the inclusions responsible for low quality.

The positive outcomes for improved quality control include increased customer satisfaction, reduced downtime which improves the likelihood of meeting and exceeding production targets, and a reduced carbon footprint as a result of waste reduction.

Solution requirements

Based on the listed business objectives and the availability of the MV20/20 system for real-time measurements, the problem can be described as:

• R₁: Develop anomaly detection for the improvement of time- to-reaction. This has considerable loss reductions in time and processing effort. This satisfies P₂.

• R₂: Develop an algorithm to determine whether a cast is a pass or fail. This partially satisfies P₁ and P₃.

• R₃: Develop a per-cast algorithm to determine the responsible inclusion type. This partially satisfies P₁ and P₃.

Hypotheses

The following hypotheses are aimed at addressing each of the requirements of the work:

• H₁-The calculation and plotting of the mean, standard deviation, min, max and variance will provide basic statistical analysis. The plotting of univariate distributions and a multivariate correlation plot will provide a comprehensive understanding on the nature of the dataset.

• H₂-This hypothesis is broken down into two parts:

a. H₂a-Univariate statistical process control charts. These charts trend the real-time data and bound it within upper and lower control limits based on 1.5 σ from the mean. An event is considered an anomaly when a point lies outside the control limits.

b. H₂b-Multivariate control chart. This chart shows a plot of the multivariate data decomposed into a 2D latent space and bounded by a 95% confidence interval ellipse. An event is considered an anomaly when a point lies outside the ellipse.

• H₃-The development of a machine learning model like a logistic regress or, support vector machine, or neural network with optimized hyper parameter tuning using 10-fold repeated cross- validation can achieve the business target metrics for a classifier.

Constraints

• C₁: The dataset available for this work is a small dataset with 378 observations from 13 numerical features. It takes time to collect each tagged observation, and the business is intent or realizing a solution within objective time frame.

• C₂: The solution is budget constrained and must be implemented using open-source technologies.

Success criteria

A summary of the success metrics for the primary classifier is given in the following Table 1.

Table 1: Success metrics for sample result target respondent.

For the secondary classifier, which classifies the responsible inclusion type in the event of a failed sample, the following metrics are to be met (Table 2).

Table 2: Success metrics for inclusion type target respondent.

The sensitivity and specificity are lower than for the primary classifier. This is because it would be more difficult to identify a single inclusion type in cases where there is more than one inclusion type present in the metal. Also, the classification of inclusions provides a benefit of faster root cause analysis, and is not directly linked to client-facing metrics.

Rationale

The South African government has been increasingly urging manufacturing plants to contribute towards a national program to improve sustainability and reduce the country’s carbon footprint. Some of the goals of the program include reduction of waste, consumed energy and runaway greenhouse gasses. As a result, the aluminum cast house has embarked on the implementation of technologies that positively contribute towards this goal.The availability of data from the MV20/20 sensor therefore presented the opportunity to implement quality control through the use of modern analytics methods. The implementation of descriptive, diagnostic and predictive analytics is deemed by the cast house as a good starting point towards making the plant more efficient and eventually more sustainable.

Outline

The remainder of this document contains the literature review, methodology applied, the experiments performed, the results and recommendations for future work.

Literature Review

The application of modern data analytics techniques including machine learning within the context of cast metal quality is relatively recent. This is mainly because most measurement techniques for cast metal rely on extraction for offline processing. This therefore limits the potential for analytics based on sensor-generated data.

Torabi Rad, Viardin, Schmitz, and Apel presented the modeling of the alloy solidification process using a theory-trained deep neural network [9]. The data is trained on simulated data points generated by simulated points based on theoretical mathematical models. Trained models can then predict solidification temperature, for example, based on input points. The novelty of the solution is in it being the first of its kind. While the solution can identify quality defects during casting, it is limited to only considering the macro-scale quality problem, and not defect trapped deep in the alloy.

In a non-destructive testing method using X-ray is used to collect training data [10]. Ellipsoidal synthetic defects are modeled and added into the training data, and a deep convolutional neural network is trained to detect and classify them. The solution works well, but would require substantial capital investment in industrial X-ray systems.

According to researchers, South Africa is among the highest producers of carbon dioxide emissions from the aluminum industry. In addition, the state-of-the-art technologies developed have been mainly focused on the improvement of the casting process. The quality improvements have been on developing better filtration systems and casting recipes. The novelty of this proposed work is in the fact that it will be the first application of business analytics (descriptive, diagnostic, predictive analytics) in the control of metal quality so as to minimize downstream processing of defective metal. Each downstream process cumulatively adds to the waste in energy and gas usage, thus contributing to the increased emissions. A faster detection of defective metal can prevent this downstream processing, which is the justification for this work.

Methodology

An analysis of the dataset indicates that the data is ready for ingestion and processing. This is based on the fact that the data is available in .csv format, which is ready for ingestion by many analytics tools. This therefore places the primary focus of the work on analysis of the data to extract insights for diagnostic and predictive knowledge. For this, the data analytics process is followed.

Data exploration

The data exploration involves ingestion, standardization, visualization and statistical analysis of the data in order to gain insight into the nature of the dataset. Once data is ingested, it is wrangled, which involves checking for missing and inconsistent values. Finally, plots are generated to visualize the behavioral patterns of the dataset. This encompasses the descriptive analytics step of the analytics process [11].

Univariate statistical process control

Univariate Statistical Process Control (SPC) is an industrial framework for statistically determining the control limits for target parameters [12]. The charts implemented in this study include individual, run and moving range. These metrics are mportant for determining the time-series trend, impulsiveness and individual behavior of critical control variables [13].

Multivariate clustering

Multivariate clustering is a technique for decomposing multivariate data into a smaller, more intuitive dataset that can be used to gain insights into the behavior of data [14]. Two techniques are considered for multivariate clustering, which have been shown to adequately cluster and provide tunability for most cases [15,16]. These techniques include K-Means and DBSCAN. The K-Means method uses principal components analysis and clusters using the Hartigan-Wong, Lloyd and MacQueen algorithms respectively. The DBSCAN algorithm is based on varying the values of ϵ to achieve an optimal configuration of clusters.

Classification

The classification involves using the sample result and inclusion type variables as target respondents respectively. For both of them, four algorithms are compared, namely logistic regression, support vector machines, multilayer perceptron and the radial basis function network. These models are among the most widely used and supported in industrial applications, mainly for their success in classification problems [17,18].

Data exploration

A summary of the input data is shown in the following Table 3. The dataset has 19 features. Of the features, 17 are numeric and 2 are categorical (inclusion type and sample result). One feature, namely LPS_160 m, is constant and is therefore discarded from the dataset. In addition, the features Mean_LPSm and Peak LPSm are derived features which are calculated and not directly measured from the system. They are also therefore discarded from the dataset.

Table 3: Input data summary.

The features “inclusion-count”, “No Signal” and “PSP1000M” have the highest ranges and consequently the highest standard deviations. This means that, in order to ensure that they do not diminish the contributions of other features to the overall variance of the dataset, standardization could be necessary to scale them to unit variance.

In order to decompose the multivariate relationships of the features, a scatterplot matrix is shown in the following Figure 1.The following scatterplot matrix shows the correlations between the features, colored by the sample result categorical respondent. The scatterplots show linear relationships between the cleanliness, MV grade and the LPS 50 μm-60 μm features. This is consistent with the fact that the MV grade is an estimate of the cleanliness without attenuation, and that the number of particles in the metal is inversely proportional to the cleanliness of the metal. The inclusion count and no signal features show no strong correlations to the other features. The “passed” category of the sample result shows a linear separation with all the features, except for some overlaps with the “failed” result around the centers. This is an indication that the cleanliness of the metal might have a strong influence on the result of the sample.

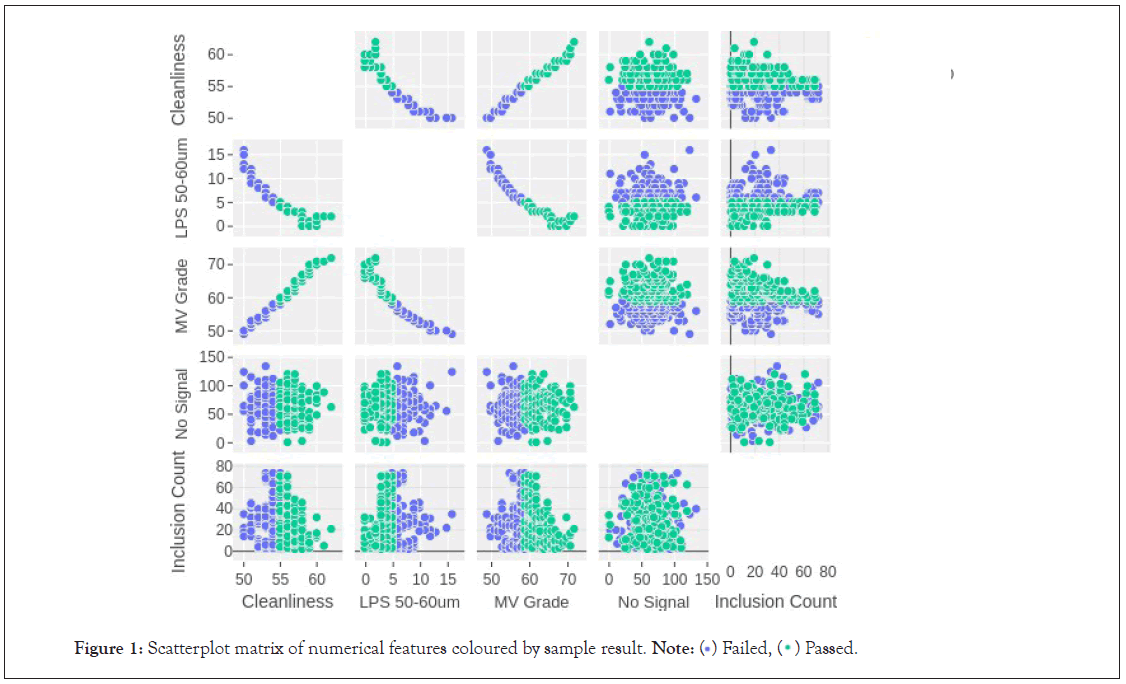
Figure 1: Scatterplot matrix of numerical features coloured by sample result. Note: Passed.

Anomaly detection

The statistical process control framework establishes upper and lower control limits for variables [12,19]. These limits can be used to form triggers for anomalous events in production. Four variables are treated as the control variables:

• Cleanliness index: The cleanliness index indicates the cleanliness of the cast.

• The largest particle size count for particles between 120 μm and 140 μm (LPS 140-160).

• The largest particle size count for particles between 140 μm and 160 μm (LPS 140-160). These two LPS variables represent the biggest sized inclusions, which are the most harmful to metal quality.

• The inclusion count: This gives an indication of the abundance of inclusions, which can indicate when an anomalous injection of inclusions becomes present in the metal.

Univariate statistical process control

The run charts for the control variables are given in the following grid plot Figure 2. As can be seen, the run charts show the time series progression of the datasets and the center lines. The individual charts for the control variables are shown in the following grid plot Figure 3.

Figure 2: Run charts for control variables of (a) Cleanliness, (b) LPS 120–140, (c) LPS 140–160, (d) Inclusion Count.

Figure 3: Individual charts for control variables of (a) Cleanliness, (b) LPS 120–140, (c) LPS 140–160, (d) Inclusion Count.

The individual charts show points outside control limits for the LPS control variables. This is an indication of points here the values were higher than 1.5 standard deviations from the center line [12]. They are correctly flagged as anomalies, and in a production environment, would prompt appropriate action and a decision for the quality of cast. In order to ensure that the system is not flooded with anomalies, however, the cast house could start off with a more conservative approach and widen the control limits, which can later be tightened as the process itself improves. The moving range charts for the control variables are shown in the following grid plot Figure 4.

Figure 4: Moving range charts for important features of (a) Cleanliness, (b) LPS 120–140, (c) LPS 140–160, (d) Inclusion Count.

The range chart also indicates anomalous events for the LPS variables, including the one point for the cleanliness. This indicates that there are jumps in the average values of the control variables, and they can be likely attributed to certain causal events that are not part of normal operations.

Multivariate clustering

It is worth mentioning that the confidence interval for the anomaly detection clusters, which is the anomaly threshold, can be configured based on domain knowledge. This is because the equipment tolerances, maintenance regimes and other factors all affect the frequency and distance of anomalies from the cluster centers. It is therefore necessary to perform a live evaluation of the best threshold distance based on the data statistics at the time. For this work, a 95% confidence interval is used, which corresponds to 2 standard deviations from the cluster center.

The k-means algorithm is a distance-based algorithm for clustering points [16]. There exist three variants of the k-means algorithm, namely the Hartigan-Wong, Lloyd and MacQueen. These algorithms are compared in the following Figure 5.

Figure 5: Moving range charts for important features of (a) Cleanliness, (b) Lloyd, (c) MacQueen. Note: 2.

• The following observations are made with respect to the k-means clusters:

• The variance accounted for by the clusters is 77.2%. This is deemed adequate to represent the variance of the data, as it accounts for over two thirds of the variance.

• There exist substantial spatial overlaps in the clusters. This can be seen on the number of points within the overlapping region.

• Most of the data is concentrated between the two clusters. This indicates that the overlapping region represents good process performance.

• The outliers constitute a minority of the data and could potentially indicate a process drift.

The k-means method is therefore considered adequate to be used as an anomaly detection technique, in which outliers can be flagged as anomalies. It is also noted that the three algorithms provided the same performance. The DBSCAN algorithm is a density-based algorithm for clustering [20]. It is applied to assess its clustering capability. The following Figure 6 shows the clustering when a small value of ϵ is applied. The minimum number of points, which is needed by the algorithm, is set at 10. The clusters are show in the following Figure 6 for different values of ϵ.

Figure 6: DBSCAN clusters for different center distances of (a) ε=5, (b) ε=10, (c) ε=15. Note:

The clusters show a gradual improvement, until a saturation point, when the distance has covered all points in the cluster at ϵ=5. At this distance, the algorithm still recognizes a substantial number of points within the 95% confidence interval ellipse as outliers. This is because it is a density-based algorithm [20].

Supervised learning classification

For supervised learning, the aim is to achieve classification by teaching algorithms using labeled datasets. The labelsused in this study are the two categorical variables, namely sample result and inclusion count. The classification metrics used to assess model performance are accuracy, precision, sensitivity and specificity [21].

Due to the dataset being small, it is split 80/20 between training and testing. The training dataset is also cross validated using 10- fold cross-validation so as to optimize the ability of the model to generalize over the data.

Logistic regression

Logistic regression uses the log it function to perform a regression, and the output is treated as a categorical outcome [22]. The repeated cross-validation loss curve for the model is given in the following Figure 7 for the sample result target respondent. The curve shows a steady increase in log-loss as alpha increases, peaking around α=0.9. The optimal value of alpha is therefore 0, where the training loss is at its lowest. The repeated cross- validation loss curve for the model is given in the following Figure 8 for the inclusion type target respondent. The curve shows that the training loss is at its minimum when α=0. This is therefore the optimal hyper parameter used to build the final model.

Figure 7: Sample Result target respondent cross-validation model training for different values of α.

Figure 8: Inclusion type target respondent accuracy model training for different values of α.

Support vector machine

The support vector machine has four main configurations, which are discussed below [23,24].

Linear: The first parameter to optimize is the linear cost function, which is common among all the variants of the SVM model. In order to find the optimum cost coefficient, a linear variant of the activation function is used, and the cost function is incremented.

Polynomial: The polynomial degree is another variant of the SVM that uses a polynomial function to separate the hyperspace. The degree of the polynomial is the hyper parameter to be optimized.

RBF: The Gamma coefficient for the radial basis function optimizes the radius of influence and therefore the sensitivity of the model to training data.

Kernel: The kernel SVM uses a kernel function to search for the optimal hyperspace. In order to compare the kernel functions, the optimal hyper parameters are set for each kernel function respectively, and the training performances of the kernel functions are compared.

The following Figure 9 shows the hyper parameter plots respectively as they are swept from zero for the sample result target.

Figure 9: SVM hyperparameters (a) Cost function, (b) Polynomial degree, (c) RBF Gamma, (d) Kernel function swept from zero for the sample result target. Note: Polynomial, ( ) RBF.

The training results reveal the following:

• The optimal cost function is determined to be 0.1 as the loss of the model is minimal at that value. This value is therefore used for all the variants of the SVM.

• The log-loss curves show that the degree of 3 is the optimal degree for the polynomial variant of the SVM model. This is because it has the lowest loss at a corresponding gamma value of 0.3. These are therefore the selected hyper parameters for the polynomial variant.

• The best performance for gamma is at 0.01, where the lowest log-loss is achieved. This is therefore used to train the final model.

• The loss functions for the different kernels show little difference in performance. The polynomial kernel appears to provide the best loss, followed by the RBF kernel. The differences are negligent, which indicates training convergence. This implies that the polynomial and RBF kernel functions can be used with negligible difference in performance. The RBF kernel, however, is more computationally expensive, and therefore the polynomial kernel is used in the final model.

The following Figure 10 shows the hyper parameter plots respectively as they are swept from zero for the inclusion type target:

Figure 10: SVM hyperparameters (a) Cost function, (b) Polynomial degree, (c) RBF Gamma, (d) Kernel function swept from zero for the inclusion type target. Note: Linear, Polynomial, RBF.

The following observations are made:

• The log-loss function sharply decreases down to a minimum of 0.395, where the cost function is 0.9. This is therefore the value used for training the SVM.

• The curves show that for higher degrees of the polynomial, the loss increases after a sharp drop atγ =0.1. The first degree is the only order to maintain a decrease in the loss function for increasing values of gamma. The lowest loss is achieved at a value of γ=1, where the loss is 0.4.

• From the curve, it can be seen that the loss function takes a sharp drop before slowly increasing. The optimal value of gamma is therefore where the loss makes a turning point, which is 0.27.

• The RBF has proven to be the optimal kernel function for fitting the data, as it offers the best overall performance in relation to the loss function. The linear and polynomial functions have comparable performance. The RBF is therefore the preferred kernel for building the final model.

Multi-layer perceptron

The multi-layer perceptron is a feed-forward artificial neural network. It is the most basic form of the neural network, where the number of neurons, the number of layers and the activation functions can be tuned [25-28]. As a start, the model is trained with one hidden layer. The number of neurons and the activation function are optimized using cross-validation. Four of the most widely used activation functions are considered for this study, so as to select an optimal function. These are.

Rectified Linear Unit (ReLU): The ReLU is the most popular activation function in neural networks. The ReLU function is the preferred starting point as it retains x for all positive values of x. This gives a safe performance regarding diminishing gradients and exploding gradients as it is non-saturating and it offers an accelerated gradient descent towards a minimum value of the loss function

Maxout: The maxout activation function is a generalization of the ReLU and leaky ReLU activation functions in that it selects the maximum value of the input. The main advantage of maxout functions is that with at least two maxout units, they can approximate any function. They have also been proven to perform well for most applications.

Linear: The linear function maps the output to the input. While for positive values of x the linear function shares the advantages of the ReLU function, its major drawback is that it does not support back propagation. This is because the derivative of the function is a constant value (1) which has no relationship to the input.

Sigmoid: The sigmoid function is an inverse of the exponential decay function. It casts any input to a value between 0 and 1. This makes it ideal for cases where inputs might be unevenly weighted, as the input contributions will not differ by much. This also means that the sigmoid can be used to predict probabilities, as probabilities only exist between 0 and 1.

The model loss functions are presented in the following Figure 11 for the sample result target:

Figure 11: Sample result target respondent multi-layer perceptron training performance for one hidden layer. The activation function and number of neurons are the optimised parameters. Note: Tanh, n=9, Maxout, n=9, Tanh, n=10.

It is difficult to tell from the model which of the combinations yields the best training performance. The maxout function with 8 neurons, however, appears to have the lowest training loss towards the last epoch [29]. The Table 4 below summaries the respective model configurations in order of increasing log-loss. As there is 46=24 models built from cross-validation, only the top 5 are presented.

Table 4: Sample result target respondent multi-layer perceptron training performance for one hidden layer.

It is evident that the maxout activation function is dominating the performance, followed by the ReLU function. The optimal number of neurons for the first hidden layer is 8, as it presents the lowest training loss. The model might be overfitting in cases where n>8. The addition of a second hidden layer, while keeping the units of the first hidden layer at the optimal value of 8, is presented in the following table.

The Table 5 indicates that an additional hidden layer improves training performance. The best configuration involves the second hidden layer with 6 neurons. Since this is a significant improvement from the training performance of the model with one hidden layer, this configuration is the preferred one for building the final model.

Table 5: Sample result target respondent multi-layer perceptron training performance for two hidden layers.

The model training performance for one hidden unit is shown in the following Figure 12 for the inclusion type.

Figure 12: Inclusion type target respondent multi-layer perceptron training performance for one hidden layer. The activation function and number of neurons are the optimised parameters. Note: Tanh, n=9, Maxout, n=9, Maxout, n=8, ( ) Tanh, n=10.

The model configurations indicate comparable training loss performances, also indicating a convergence condition. The following Table 6 shows the model configurations ordered by increasing log-loss. The maxout activation function dominates the performance for the single hidden layer configuration of the model, followed by the tanh function. It is therefore the optimal activation function used in building the final model. The second hidden layer is added to the configuration, and the training results are shown in the following Table 7. The performance for the configuration with the second hidden layer shows only a slight improvement from the configuration with a single hidden layer. This means that the configuration with a single hidden layer can be used without compromising too much training loss [30].

Table 6: Sample result target respondent multi-layer perceptron training performance for one hidden layer.

Table 7: Inclusion type target respondent multi-layer perceptron training performance for two hidden layers.

Radial basis function network

Radial basis function networks are a specialisation of neural networks with a radial basis function as the activation function. They have been shown to have success in many cases where the boundary conditions are more complex [31-36]. The negative threshold tuning by means of repeated cross-validation is shown in the following Figure 13 for the sample result target. The loss curve shows a dip at 0.8 and a sharp incline. The optimal threshold is therefore 0.8. The negative threshold tuning by means of repeated cross-validation is shown in the following Figure 14 for the inclusion type target. The log-loss function has its minimum at a threshold of 0.2, before it steadily increases. The optimal threshold used is therefore 0.2.

Figure 13: Sample result target respondent RBF training performance.

Figure 14: Inclusion type target respondent RBF training performance.

Discussion

In this section, the models are tested on the test data split from the training data. The test data consists of 126 observations and constitutes 25% of the total data. The test results are presented in the form of a confusion matrix, which quantifies how well the model performs on unknown data. Within the context of unsupervised learning, tests data does not exist as all the data is unlabeled. This therefore means that unsupervised learning models have to be applied with domain knowledge in order to ensure the anomalies represent real life anomalies.

Supervised learning classification

The following Table 8 shows a side-by-side comparison of the models for the sample result target. The following Figure 15 shows the comparison between the models.

Table 8: Model performance comparisons for sample result target respondent.

Figure 15: Model performance comparisons for the sample result target respondent. Note: Support vector machine, Multilayer perception, Radial Basis function networks.

• The logistic regression model has performed satisfactorily as it satisfied the metrics except for accuracy, where it achieved 0.4% below the target. This is within the 95% confidence interval, so it is considered a success.

• The SVM model gave a better overall performance than the logistic regression model. It achieved a higher score for each of the performance metrics, with a perfect score for sensitivity. It is therefore regarded a success.

• The MLP model has so far shown the best performance as it has exceeded all the target scores.

• The RBF network model has also exceeded all target scores, although its performance is slightly below that of the MLP.

The models have all shown the capability to generalize well over the training data [31]. This can be seen in the fact that the confusion matrices have shown good scores in testing performance over data that the models have not seen before. The logistic regression model, while the worst performing from the four is still within the 95% tolerance of the target metrics. The MLP, SVM and RBF network models all performed well. The MLP gave the best performance, and is therefore recommended as the model to use. This is because the costs associated with each false alarm or miss are high within the context of an aluminum manufacturing factory. Each loss can potentially cost the business hundreds of thousands of rands. For the multiclass problem, the metric scores are presented per class, so as to assess the performance of the model over individual classes in addition to the overall performance. The following Table 9 shows a side- by-side comparison of the models. The following Figure 16 shows the comparison between the models. The results show that the logistic regression model has scored below the target overall, except for specificity. Even for specificity, the per-class scores show that it achieved 0.63 for the SPINEL inclusion type, which is below target by 0.13. The best scores achieved are for FeO, which are also below target. This makes sense as the value of α=0 reduces the model to a constant log it functions which is insensitive to the input.

Table 9: Model performance comparisons for sample result target respondent.

Figure 16: Model performance comparisons for the sample result target respondent. Note: Logistic regression, Support vector machine, Multilayer perception, Radial Basis function networks.

The SVM performance is better than the performance of the logistic regression model, with all the overall scores higher for the SVM than the logistic regression model. The model, however, did not meet all targets. The model scored above target only for the specificity class. The scores for accuracy, precision and sensitivity are not as far below target as for the logistic regression model. The value of kappa also indicates that there is substantial value in the model agreement with the dataset, as opposed to a completely random guess of the data [35]. The model, however, is considered inadequate as it does not satisfy the target metrics.

The MLP is once again showing the best performance so far, with targets for precision, sensitivity and specificity met. The accuracy is slightly below target, but is still within the tolerance. The sensitivity and specificity have been well exceeded, as the model especially gave few erroneous predictions for the SPINEL class. The MLP model is therefore considered a success.

The RBF network model performance is worse than that of the MLP model for all the metrics. This implies that the application of radial basis functions as activation functions for the classification of inclusions gives a worse performance than applying maxout functions, which are used in the MLP. The problem of generalizing over the inclusion types has proven to be much more difficult to solve than predicting the outcome of the metal quality. This might be attributed to the following:

• The attenuation caused by the different inclusions is similar from an ultrasonic point of view.

• The inclusion sizes and counts for the different classes are similar and not easily separable. This could be due to the filter that the metal passes through just before the casting stage.

• The results of the metallographic analysis used to classify the inclusions are not entirely reliable due to operator error.

• The MLP can therefore be considered as it provides the best results, and subsequent tuning of the model can improve performance.

Performance optimisation

The previous subsection has shown that all the models are capable of providing good predictions over the sample result target respondent. The same cannot be said for the inclusion classification problem, as the prediction scores for the models were largely below target. In order to improve the model, hyper parameter tuning is considered with even more parameters.

Hyperparameter tuning

The best performing model, namely the MLP, is tuned further in this section with the intention of assessing whether an improvement in performance can be achieved. In order to achieve this, more tuning parameters are iterated over using repeated cross-validation [37]. It should be noted that the tuning of more hyper parameters does not guarantee an improved performance, but it is worth exploring for the potential improvement. The parameters are given in the following Table 10.

Table 10: Multi-layer perceptron model hyperparameters.

The additional parameters from the table include:

Epsilon: Which changes the selection randomness probability for the learning gradient a large value of ϵ would mean that the learning diverges, while a small value would mean the learning converges too slowly.

• L1: Which is the Lasso regularization parameter it ensures that the model is penalized for learning loss so as to minimise the effect of some weights [38]. A high value of L1 would see more weights being set to zero.

• L2: Which is the Ridge regularization parameter it also penalizes the cost function, but never sets the weights to zero [38].

• Rho: Which is the learning rate decay factor it is responsible for ensuring that the gradient descent is smooth [39,40]. Higher values of ρ tend to give better smoothing results.

Hyperparameter search

There are three most widely used methods for finding optimal configurations of the model hyper parameters, namely grid search, random search and genetic algorithm (evolution) [41].

Grid search: The grid search method entails an exhaustive sweep through the hyper parameter grid space in order to find the point that offers the lowest training loss [42]. This method is relatively expensive and could take a long time for big datasets. It does, however, guarantee a global maximum.

Random search: Another optimization method is random search, which performs random combinations of hyper parameters in order to find an optimal combination [43]. The random search method is not guaranteed to produce optimal results as it samples a subspace of the hyper parameter grid, and might therefore not find the global maximum.

Genetic algorithm evolution: The genetic algorithm simulates evolution by natural selection in that it selects for the hyper parameter values that provide better results, and selects against those that don’t. Those that are selected for are used in the next round, which is the next point on the search grid [44-48]. The genetic algorithm eventually converges at an optimal point on the grid, although this might take time and the point might not be a global maximum. For this work, the grid search method is used as it guarantees the best results. The dataset is also small and therefore can be iterable within reasonable time. The grid search produced 187,500 models based on the given hyper parameters.

The results revealed the following points:

• The number of hidden layers does not significantly improve the performance of the model beyond neurons. It is therefore confirmed that keeping the number of neurons at 8 and applying the law of universal approximation (one hidden layer) is sufficient for achieving an optimal model.

• The regularization parameters l1 and l2 do not have a significant effect on the training performance of the model. This can be seen in the grid search plot, where their values are closely related with respect to the loss function of the model.

• The gradient descent term ρ has an inversely proportional relationship with the training loss of the model. It can therefore be set at its highest value in order to achieve the lowest training loss.

• The selection randomness probability ϵ has an inversely proportional relationship with the training loss of the model. It can therefore be set at its highest value in order to achieve the lowest training loss.

The following Table 11 shows a summary for the parameters for the top 5 models based on the lowest training log-loss. Based on the table, it can be seen that the training performance of the model does not improve much as the hyper parameters are changed. It should also be noted that the training performance of the model is comparable to that of the multi-layer perceptron prior to the employment of a grid search.

Table 11: Grid search model log-loss performance.

Final model results

The model is built based on the best parameters, and tested on the test data. The following confusion matrix shows the performance of the model Tables 12 and 13. Based on the confusion matrix and metric scores shown in the table, the following observations are made:

Table 12: MLP model performance after grid search of confusion matrix.

Table 13: MLP model performance after grid search of metric scores.

• The model after grid search is not much better than the model before grid search. This is most likely an implication of the model having reached its learning potential.

• The MgO inclusion has the worst performance. The metrics are below target except for specificity. This implies that the model is not able to generalize well over this inclusion type.

• The SPINEL inclusion type is within the target limits except for the precision metric. For the other metrics, it has exceeded targets.

• The FeO inclusion type has the best performance and has exceeded the targets for all metrics.

The model does not therefore generalize well over the inclusion types. A plot of the model’s decision boundaries is shown in the following Figure 17.

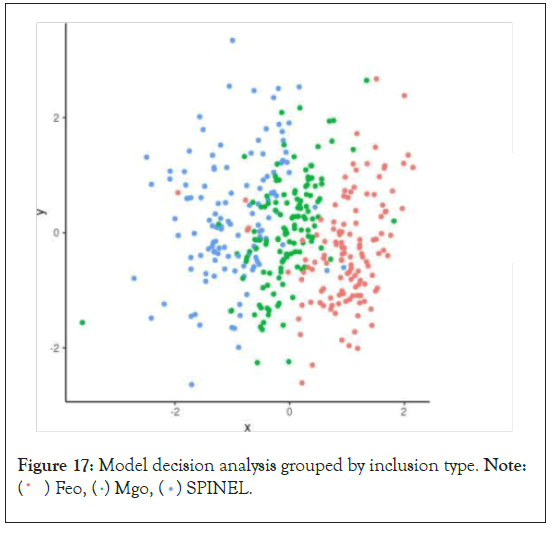
Figure 17: Model decision analysis grouped by inclusion type. Note: SPINEL.

CONCLUSION

An opportunity has been identified in an aluminum manufacturing plant to improve quality control by means of a pulsed ultrasound system. This system is capable of performing real-time measurements on molten metal, which reveal the cleanliness of the metal. In order to automate the process of accepting the metal as clean, unsupervised and supervised learning approaches are applied. The unsupervised component of this project focuses on anomaly detection for real-time alerting of operators and relevant personnel. This is achieved by exploring dimensionality reduction techniques including principal components analysis, K-means and DBSCAN clusters. A 95% confidence interval ellipse is drawn around the cluster as a means of identifying potential and would-be outliers.

The supervised learning component involves the development of a two-stage classifier. The first stage determines whether the metal quality is adequate for production. The second stage determines the dominant inclusion responsible for the quality deterioration. Four models are trained, namely logistic regression, support vector machine, multi-layer perceptron and a radial basis function network. While the inclusion type classifier gave a boundary performance on accuracy and precision, the values are within the 95% tolerance range. The project is therefore considered a success. During casting, the metal forms a thin oxidization layer on the surface, which is an indication of the presence of some inclusions at the top of the metal. A vision system can be employed to analyze the texture, color and other visual properties of the metal in order to provide more insights relating to the nature of inclusions, the intensity of the inclusions and the effects of different casting parameters on the texture of the metal.

The attenuation levels of inclusions compared to pure aluminum could produce different infrared signatures, which could be measured and analyzed using Fourier Transforms. This is because different elements possess different reflectance and attenuation properties at different wavelengths. Classifiers can then be built to determine the types and intensities of inclusions based on the spectral properties of the measurements.

Author Contribution

All authors contributed equally to this work.

Acknowledgement

None

Conflict of Interest

Authors declare no conflict of interest.

References

1. Gallo R. Differentiating inclusions in molten aluminum baths and in castings. Pyrotek Inc. OH, USA. 2017.
2. Eckert CE, Cochran B. The importance of metal quality in molten secondary aluminum. Recycling of Metals and Engineered Materials. 2000:919-22.

   [Crossref] [Google scholar]

3. Differentiating inclusions in molten aluminum baths and in castings
4. Veillette D, Paquin D. Metallographic analysis. International Aluminium Casting, Canada. 2006.
5. Zurich O. Mobile liquid aluminium cleanliness analyser. 2017.
6. The importance of metal quality in molten secondary aluminum
7. Smith DD, Hixson B, Mountford H, Sommerville I. Practical use of the metalvision ultrasonic inclusion analyzer. Light Met. 2015;937-942.

   [Crossref] [Google scholar]

8. Gallo R, Mountford H, Sommerville I. Ultrasound for on-line inclusion detection in molten aluminum alloys: Technology assessment. In Proc. 1st International Conference on Structural Aluminum Castings. 2003;1-16. 

   [Google scholar]

9. Rad MT, Viardin A, Schmitz GJ, Apel M. Theory-training deep neural networks for an alloy solidification benchmark problem. Comput Mater Sci. 2020;180:109687.

   [Crossref] [Google scholar]

10. Mery D. Aluminum casting inspection using deep learning: A method based on convolutional neural networks. J Nondestr Eval. 2020;39(1):1-2.

    [Crossref] [Google scholar]

11. Start SH. Introduction to data analysis handbook migrant and amp seasonal head start technical assistance center academy for educational development. Int J Acad Res. 2006;2(3):6-8.

    [Google scholar]

12. Pyzdek T, Keller PA. A complete guide for green belts, black belts, and managers at all levels.

    [Google scholar]

13. Wild CJ. Chance encounters: A first course in data analysis and inference. 

    [Google scholar]

14. Agrawal S, Agrawal J. Survey on anomaly detection using data mining techniques. Procedia Comput Sci. 2015;60:708-713.

    [Crossref] [Google scholar]

15. Hodge V, Austin J. A survey of outlier detection methodologies. Artif Intell Rev. 2004;22(2):85-126.

    [Crossref] [Google scholar]

16. Celebi ME, Kingravi HA, Vela PA. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst Appl. 2013;40(1):200-210.

    [Crossref] [Google scholar]

17. Kiang MY. A comparative assessment of classification methods. Decis Support Syst. 2003;35(4):441-454.

    [Crossref] [Google scholar]

18. Suykens JA, Signoretto M, Argyriou A. Regularization, optimization, kernels, and support vector machines. CRC Press. 2014.

    [Croosref] [Google scholar]

19. Gareth J, Daniela W, Trevor H, Robert T. An introduction to statistical learning: With applications in R. Spinger. 2013.

    [Google scholar]

20. Ester M, Kriegel HP, Sander J, Xu X. A density-based algorithm for discovering clusters in large spatial databases with noise. Inkdd 1996;96(34):226-231.

    [Google scholar]

21. S. Minaee. 20 Popular machine learning metrics. part 1: Classification and regression evaluation metrics. 2019.
22. Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol. 1996;49(12):1373-9.

    [Crossref] [Google scholar] [PubMed]

23. Hsu CW, Chang CC, Lin CJ. A practical guide to support vector classification.2010.
24. Hastie T, Tibshirani R, Friedman JH, Friedman JH. The elements of statistical learning: Data mining, inference, and prediction. Springer. 2009.

    [Crossref] [Google scholar]

25. Goodfellow I, Bengio Y, Courville A. Deep learning. MIT press. 2016.
26. Abraham A. Artificial neural networks. Handbook of measuring system design. 2005.

    [Google scholar]

27. P. Baheti. 12 Types of Neural Network Activation Functions: How to Choose? V Labs. 2021.
28. Goodfellow I, Warde-Farley D, Mirza M, Courville A, Bengio Y. Maxout networks. In International conference on machine learning 2013.1319-1327.
29. Kawaguchi K, Kaelbing LP, Bengio Y. Generalization in deep learning. 2020.
30. Wu Y, Wang H, Zhang B, Du KL. Using radial basis function networks for function approximation and classification. Int Sch Res Notices.2012.

    [Crossref] [Google scholar]

31. Park J, Sandberg IW. Universal approximation using radial-basis-function networks. Neural Comput. 1991;3(2):246-57.

    [Crossref] [Google scholar]

32. Karayiannis NB. Reformulated radial basis neural networks trained by gradient descent. IEEE Trans Neural Netw. 1999;10(3):657-71.

    [Crossref] [Google scholar]

33. Moody J Darken CJ. Fast learning in networks of locally-tuned processing units. Neural Comput. 1989;1(2):281-94.
34. Oliveira AL, Melo BJ, Neto FB, Meira SR. Combining data reduction and parameter selection for improving RBF-DDA performance. In Ibero-American Conference on Artificial Intelligence 2004. 778-787.

    [Crossref] [Google scholar]

35. Nwankpa C, Ijomah W, Gachagan A, Marshall S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv. 2018.

    [Crossref] [Google scholar]

36. Tran N, Schneider JG, Weber I, Qin AK. Hyper-parameter optimization in classification: To-do or not-to-do. Pattern Recognit. 2020;103:107245.

    [Crossref] [Google scholar]

37. Sun X. The Lasso and its implementation for neural networks. University of Toronto. 2000.

    [Google scholar]

38. Guo C, Pleiss G, Sun Y, Weinberger KQ. On calibration of modern neural networks. In International conference on machine learning. 2017.1321-1330.

    [Google scholar]

39. You K, Long M, Wang J, Jordan MI. How does learning rate decay help modern neural networks? ArXiv. 1908.01878. 2019.

    [Crossref] [Google scholar]

40. Liashchynskyi P, Liashchynskyi P. Grid search, random search, genetic algorithm: A big comparison for NAS. ArXiv. 1912.06059. 2019.

    [Crossref] [Google scholar]

41. Pontes FJ, Amorim GF, Balestrassi PP, Paiva AP, Ferreira JR. Design of experiments and focused grid search for neural network parameter optimization. Neuro computing. 2016;186:22-34.

    [Crossref] [Google scholar]

42. Andradóttir S. A review of random search methods. Handbook of Simulation Optimization. 2015:277-92.

    [Crossref] [Google scholar]

43. Simon D. Evolutionary optimization algorithms. John Wiley and Sons. 2013.

    [Google scholar]

44. Badar AQ. Evolutionary Optimization Algorithms. CRC Press. 2021.

    [Crossref] [Google scholar]

45. Brough D, Jouhara H. The aluminium industry: A review on state-of-the-art technologies, environmental impacts and possibilities for waste heat recovery. Inter J Thermofluids. 2020;1:100007.

    [Crossref] [Google scholar]

46. Rana IA, Rehman CA. Past, present and future of business analytics-a review. Int J Manag Bus Res. 2014;3(9).

    [Google scholar]

47. Duan Y, Cao G, Edwards JS. Understanding the impact of business analytics on innovation. Eur J Oper Res. 2020;281(3):673-86.

    [Crossref] [Google scholar]

48. Bayrak T. A review of business analytics: A business enabler or another passing fad. Procedia Soc Behav Sci. 2015;195:230-9.

    [Crossref] [Google scholar]