Journal of Oceanography and Marine Research
Open Access
ISSN: 2572-3103
ISSN: 2572-3103
Research Article - (2017) Volume 5, Issue 1
In this work we study the exchange processes in the Baltic Sea during a 10-year period (2000-2009). The study is based on numerical simulations of the hydrodynamics that are verified by salinity and temperature data. A particle tracking approach is used for characterising transport and exchange processes. Inert particles are released at different rates ranging from 100 to 5000 particles at durations ranging from 10 days to 10 years with the purpose of quantifying the inter-exchange processes between the Baltic Sea sub-basins and to estimate arrival times and pathways of particles released from the major rivers. The Gotland basins are the major contributors to the baroclinic exchange process in the Baltic Sea. There is evidence in support of notable mixing of the deeper waters of the Western Gotland Basin with the sub-surface waters of the Gulf of Finland. The transport processes in the Bornholm and Arkona basins are both advective and diffusive driven by the interacting flows of the northern basins of the Baltic Sea and the North Sea. The various sills and channels play a significant role in controlling the exchanging processes of the sub basins of the Baltic Sea. Two relative measures (indicators) are introduced for quantifying internal exchange between major basins and internal distribution between basins of tracers discharged by eleven major rivers. The Sea of Bothnia is found to be the major collector basin and the Bornholm Basin the major diffusor basin of the Baltic Sea. The surface waters of the rivers mix internally with the mixing and pycnocline layers. The Gulfs of Finland and Riga, and the islands of the Archipelago Sea are probably the most vulnerable regions from an ecological point of view. The worst scenario for river-borne pollutants is a combination of short travel time and maximum travelled path; rivers of Vistula and Oder fall into this category.
<Keywords: Tracer transport; Baltic Sea; Archipelago Sea
Three major factors control the hydrodynamics of the Baltic Sea: i) Water exchange with the North Atlantic, ii) Freshwater inflow that takes place over the entire coast; iii) Bottom topography [1]. The drainage basins of the Baltic Sea discharge annually 440 km3 of freshwater and host a population of 85 million in nine countries. The anthropogenic pressures on the Baltic Sea are thereby significant and on the rise. Nutrient levels in the water and sediments are high, for instance, such that poor oxygen conditions and “dead bottoms” are found in large archipelago areas of both Sweden and Finland [2]. Implementation of common management strategies by surrounding countries aimed at minimising or reversing negative water quality trends in the Baltic Sea, still poses a number of challenges; understanding internal material transport and exchange between potential sources and receptors in the basins, coastline areas and rivers is one such challenge (Baltic Marine Environment Protection Commission http://www.helcom.fi).
In view of the large spatial and temporal variability that is known to characterise the Baltic Sea, models have been indispensable for a deeper understanding of its flow and transport properties. The large-scale transport of fresh and salt water in the Baltic Sea (“conveyer belt”) was studied by releasing particles at the North Atlantic inflow-outflow boundary (saltwater) and at the Neva river inflow boundary (freshwater) [3]. The period of the study was 1980-1993, where monthly river discharge was used as part of the forcing and water residence time was computed for salt- and freshwater particles separately. The study of Döös et al. [3] provided a clear representation of the overall transport processes in the Baltic Sea. A detailed study of residence times in two bays of the Baltic Sea (Gulf of Riga and Gdansk Bay) was presented by Jönsson et al. [4] using a similar methodology as Döös et al. [3]. Long-term water age in the Baltic Sea was investigated by Meier [5,6] based on the theory of Deleersnijder et al. [7], with repeated integration of the period 1980-2004. Water age for salt-and freshwater was computed for saltwater originating at the North Atlantic boundary, while different freshwater sources were considered (a few individual rivers, as well as simultaneous freshwater input from all rivers). The significant advancement presented by Meier [5,6] was to quantify the long-term accumulation of tracer mass injected from all rivers, in eight major basins of the Baltic Sea, distinguishing the accumulation below and above the halocline.
Kjellsson and Döös [8] discussed recent advances in surface drifts for the Baltic Sea. They computed the trajectories using a Lagrangian trajectory method proposed by Döös [9]. The trajectories were analysed by a statistical comparison with trajectories of Surface Velocity Program (SVP) drifters. The absolute dispersion or the distance from the initial point as a function of time was found to be underestimated by the model trajectories, although the overall agreement between model and observations was reasonable. The relative dispersion was found to depend on the model resolution as well as on the initial separation of the model trajectory pairs. Corell and Döös [10] studied the differences in particle transport between two coastal areas in the Baltic Sea by applying a high-resolution trajectory model. They used high-resolution ocean flow data to investigate transport of particles released at two specific locations on the Swedish coast in proximity of candidate sites for geological disposal of high-level nuclear waste (Forsmark and Simpervarp). Soomere et al. [11] studied particle trajectories in the Gulf of Finland focusing on the effect of surface currents. They found an intense net transport that occurs along the coast in the western and central parts of the gulf.
In addition to studies of the Baltic Sea [3,4,6,8,10,11] that all use the Rossby Center Ocean (RCO) model [1,12,13], other modelling approaches have been developed. Lehmann and Hinrichsen [14] presented an alternative hydrodynamic model (Kiel Baltic Sea Ice Ocean model, BSIOM), and investigated circulation and upwelling. BSIOM was recently used by Lehmann et al. [15] for identifying areas in the Baltic Sea that may be vulnerable to pollution from accidental spills along major shipping lanes. They linked statistically the shipping lanes (sources) to coastal areas (receptors) by particle tracking and found that contaminant spreading was mainly dependent on atmospheric conditions and wind-induced local sea surface currents. Engqvist et al. [16] investigated transport within a central region of the Baltic Sea, with tracers originating from a hypothetical geological waste repository site (Forsmark), using a hydrodynamic model referred to as AS3D that was presented by Engqvist and Andrejev [17] and Andrejev et al. [18]. Tracking of passive particles has been used for characterising transport in surface water under a variety of conditions [19-23]. Frequently, particle tracking is used for identifying pathways and quantifying travel times of tracers released into a surface water body.
Current studies have significantly improved our understanding of material transport in the Baltic Sea on the basin scales [6,15], as well as on regional and local [4,8,10,11,16]. Accumulation of river-borne tracers into major basins of the Baltic Sea is particularly illuminating as it seems to indicate persistence of relative accumulation over long period of time [6]. The study of Lehmann et al. [15] on the other hand emphasised the need for linking the potential sources and receptors of pollution, in this case related to intensify shipping in the Baltic Sea. What is still lacking however is better knowledge of the internal exchange between the major Baltic Sea basins?
In this study, we wish to fill this knowledge gap by answering the following questions not addressed previously: i) How large is the relative internal exchange between the major basins of the entire Baltic Sea? ii) What is the relative internal distribution of river borne (external) inputs to the Baltic Sea? Leppäranata and Myrberg [24] suggest 12 basins whereas Meier [6] considers eight basins; in our analysis twelve basins and eleven major rivers are considered which provide a basis for a source-receptor matrix representation of the exchange processes. Tracer sources were released in the central locations of each basin and at the discharge points of 12 major Baltic Sea River. Hydrodynamics is resolved in three dimensions for a 10 year period 2000-2009, using a general-purpose surface water model (Generalized Environmental Modelling System for Surface waters, GEMSS) [25-28] with a mean horizontal resolution of 8.2 × 9.2 km and 40 vertical layers. Water levels, salinity and temperature are verified against available data at a number of observation stations. Daily river discharge is used wherever available and tracer particle trajectories that account for convective movement and random dispersive processes are computed. Particle trajectories are illustrated for a broad range of source conditions and locations. From the computed trajectories and particle positions at given times, the Baltic Sea internal exchange is quantified by simple measures or indicators, representing entries in a source-receptor matrix. These measures provide a general characteristic of passive tracer exchange for the entire Baltic Sea and can be used in applications for assessing large-scale dispersion of potential pollutant sources, either in the sea or from major rivers.
The Baltic Sea is the largest semi-enclosed sea in the World that is typically viewed as composed of basins and straits with complex physical, biochemical and ecological properties [24,29,30]. It is a shallow and brackish sea located in northern Europe from 53°N to 66°N latitude and from 20°E to 26°E longitude (Figure 1). The Baltic Ice Lake was born 13,000 years ago and its present brackish state initiated 7,000 years ago. Since 2,000 years ago, salinity has been close to the present level (mean salinity 7 parts per thousand abbreviated henceforth as ppt). The maximum length and width are 1,600 km and 193 km, respectively. The surface area is 377,000 km2 with an average depth of 55m, and a water volume of 20,000 km3. Its maximum depth is 459 m, which is located between Stockholm and the Island of Gotland. The Sea consists of a series of interconnected basins through narrow sills and is connected to the Atlantic Ocean via the Danish Straits. The Sea is divided into 12 basins as shown in Figure 2, which is based on Fonselius [31] interpolation. The depths vary significantly in the range of 50-440 m among these basins. In some island regions, the depths are much lower with a range of 5-20 m, especially in the Archipelago Sea, which is dominated by a large number of islands. The existence of the basins with such a significant span of depths is an important variable that should be correctly accounted for in quantifying the hydrodynamics of the Baltic Sea. In the present study, the southern region of the model is limited at 54°N, which is in the Arkona basin.
Figure 2: The Baltic Sea basin system redrawn from interpolated figure [24].
The materials used to model the Baltic Sea consisted of basic geometrical and various flow and meteorological data for the period 2000-2009 as listed below:
• The shoreline and the bathymetry in GIS format.
• Daily flow discharges for 24 Swedish and 38 Finnish rivers.
• Monthly mean flow discharge for the nine East European rivers.
• Water temperature for all the rivers.
• The forcing meteorological data (air temperature, dew point, cloud cover, pressure, wind speed, and wind direction) at 3-h intervals both as grid data and point data.
• Precipitation as rain intensity at 19 stations at daily intervals.
• Water quality data at 15-day intervals for 22 different stations spread across the sea (Figure 3). The data included water temperature, salinity, dissolved oxygen (DO), and phosphate (PO4).
• Water level observations at several stations across the sea, with the note that the monitoring stations are all located close to the Swedish eastern shorelines except for the station Visby (Figure 3).
The main data sources were the Swedish Meteorological and Hydrological Institute (SMHI) and Finnish Meteorological Institute (FMI). The gridded meteorological data were obtained from: www.smhi.se/sgn0102/bhdc/metdata_3h_grid.html.
Among many variables that affect the hydrodynamics of a large water body, the bathymetry and inflow of freshwater are the most important ones. Thus, special attention was given to improving the quality and reliability of the bathymetric data. The digitalised bathymetry of the Baltic Sea is available from two different data sets, i.e., IOW (Leibniz-Institut für Ostseeforschung Warnemünde, IOW) and SRTM (Space Shuttle Radar Topography Mission). The present study uses the IOW data set partly due to its frequent use in previous models of the Baltic Sea and partly since it better agrees with the published bathymetry maps. IOW was created by the Leibniz Institute for Baltic Sea Research Warnemünde (http://www.io-warnemuende.de/topography-of-the-baltic-sea.html). The IOW data consist of two integrated bathymetries, one with 2-km grid resolution covering the entire sea and the other with a roughly 1 km grid resolution that only covers the south-western part of the sea. Using the raw IOW data set for generating the various numerical model grids and the interpolated bathymetries caused some unforeseen difficulties. The data set worked poorly in resolving the various channels along the shorelines of Finland, and Stockholm Archipelago. The Åland Sea and its archipelago were also poorly reproduced. The latter problems caused a significant flow blockage in the forenamed 8 areas. To resolve the forgoing issues, the bathymetry was refined using several different resolutions ranging from 50 m to 400 m that depended upon the model regions. The present study uses the 250 m resolution that resolves depths ≥3 m. The ARCGIS software was extensively used for local refinements and the overlay on the coarser bathymetry.
Description of the numerical model
A three-dimensional, time-dependent hydrodynamic model GEMSS (Generalized Environmental Modelling System for Surface waters) was used. GEMSS is a general-purpose integrated system of 3D hydrodynamic and transport models embedded in GIS. GEMSS is in the public domain and has been used for environmental studies throughout the United States and worldwide. Edinger and Buchak [32,33] first presented the theoretical basis of the model. Improvements to the transport scheme, construction of the constituent modules, incorporation of supporting software tools, GIS interoperability, visualization tools, Graphical User Interface (GUI), and post-processors have been developed by Kolluru et al. [25-28]. The hydrodynamic and transport relationships are developed from the horizontal momentum balance, continuity, constituent transport and the equation of state. Higher-order turbulence closure schemes (2-equation model, and second-moment closure model by Mellor and Yamada [34]) are also included. The longitudinal and lateral coefficients are scaled to the dimensions of the grid cell using the dispersion relationships field developed by Okubo [35] and modified to include the velocity gradients of the velocity field using the Smagorinsky [36] relationship. GEMSS uses a curvilinear variably spacing horizontal staggered finite difference grid, which is based on control volume, with the elevation and constituent concentration computed at cell centres and velocities through a cell interface. Z-level with variable thickness is used for defining the grid in the vertical direction. The wave effect on the bottom shear stresses is modelled using the method of Grant and Madson [37,38]. Additional details of the model can be found in the technical documentation of GEMSS [39]. GEMSS has been applied successfully in several environmental studies [40-42].
Model setup
The model setup involved several main steps of creating the model grid, interpolating the bathymetry into the grid, defining the boundary conditions that include river inflow, water levels, precipitation, and forcing meteorological conditions. To create the model grid, non-uniform boundary-fitted curvilinear cells in a horizontal plane (x,y) and non-uniform rectangular cells in the vertical plane were used. The grid was created with a mean cell resolution of 8.2 × 9.2 km i.e., 105 × 135 cells (Figure 4). Z-layer consisted of 45 non- uniform layers with 9/1.5 m, 8/4 m, 4/5 m, 9/6 m, 9/8 m, and 6/12 m (number of layer/ layer thickness). The layers were selected to have a finer vertical grid resolution within a depth of 100 m below the surface which covers almost 80% of the Baltic Sea bathymetry. Depths below 260 m are about 0.25% of the seabed area.
The model boundary conditions consisted of discharge, head (water levels), precipitation, and meteorological forcing conditions. The corresponding data were used with the highest available time resolutions. The discharge conditions were defined by using 71 rivers that enter the modelled region with a mean discharge greater than 2 m3/s. The mean discharges vary from 2.83 m3/s (the river Kymijoki, Finland) to 2500 m3/s (the River Neva, Russia). It is assumed that the rivers enter through the water surface grid in the model (i.e., 2 to 3 grid cells). The water level was set at the open boundary with the North Sea as shown in Figure 1 with a red line (≈104 km wide). The GPS coordinates are 54°28’ N 12°50’ E and 55°22’ N 13°03’ E, in south and north directions, respectively. To set the water level, the data at the gauge station Skanör (55°26’ N 12°50’ E) were used. Two types of radiation condition and second order derivative were applied. Radiation boundary condition allows the passage of transient events through a non-reflective boundary [43]. Second order derivative refers to the case of the flow going out of the model domain. The constituent value at the boundary cell is computed by setting second derivative in that direction to zero.
The latter required the wave celerity that was estimated as the square root of gravity times the mean depth across the open boundary. The water temperature and salinity were set using the water quality data at the gauge station By1 (Figure 3). The two foregoing stations were the closest available locations to the open boundary.
The precipitation data in mm/day was applied regionally to the model. This was done by dividing the Baltic Sea surface into 19 regions, each region with its corresponding rain intensity. To define the metrological forcing conditions gridded data were used which cover the whole Baltic drainage basin with a resolution of (1 × 1º) squares. The grid extends over the area: Latitude N 49.5º-71.5º and Longitude E 7.5º-39.5º. The gridded data covers 40 years starting from 1970. Here, the gridded wind speed is the geostrophic wind. The open surface wind speed is approximated by a linear relation between the surface wind and geostrophic wind [44]. In the present study the tides are not modelled. According to the SMHI (http://www.smhi.se/en/theme/tides-1.11272) the tides in the Baltic Sea are of little significant i.e., a few centimeters variation. The waves coming from the North Sea are effectively dampened by the friction of shallow water at the entrance to the Baltic Sea. The other factor is the relatively small size of the water basin.
The simulations use fully transient boundary conditions described in the foregoing paragraph. The coupled wave model is used which besides modelling the waves, accounts for the wave influence on the bed shear stresses. Three key steps in the modelling were model initialization, the choice of numerical schemes, and the actual simulations.
The model initialization is an important part of any hydrodynamic simulation especially in the case of large water bodies such as the Baltic Sea. The long residence times make the model output sensitive to the choice of the method. In the present study, two different methods of zero and present conditions were employed. In the former case, the model was started with a uniform zero salinity and an average water temperature of 10ºC. At the open boundary, the data from the gauge station by 1 were used to set the water levels. In the second method, all the available water quality data were used.
In the present study, the 2-Equations turbulence closure model was employed based on the formulation of Mellor and Yamada [34] and the momentum and dispersion coefficient formulations [35]. The latter is modified to include the velocity gradients of the velocity field using the Smagorinsky [36] relationship. Surface heat-exchange is computed term by term [45]. The transport model uses the higher accuracy scheme known as Quick [46].
The model calibration for year 2000 was done using all the 22 monitoring stations shown in Figure 3. The temperature, salinity, and water levels field data were used. The calibration procedure involved a systematic two-step approach with the focus on temperature and salinity profiles as follows:
1. Initiating the model using the data available at all the monitoring stations for water temperatures and salinities.
2. Examining the sensitivity of the calibrated results to the choice of the initial values.
In step 1, the first day records of temperature and salinity profiles at 21 monitoring stations (Figure 3) are used as the starting conditions for the model. The RMS (Root-Mean Square) errors of temperature and salinity were then evaluated. In Step 2 the model was re-run with new sets of initial data that were successively adjusted to lower the RMS values. The adjustment involved multiplying temperature and salinity values by factors between 1.1 and 1.5. The procedure significantly improved the agreement with the measurements with a relative error range of 10-20% for both temperature and salinity.
Figure 5 shows a typical calibration result at F3 for different depths (i.e., surface, 4 m, 12 m, 40 m, 60 m, and 80 m). The surface refers to the centre point of the Z-grid, which is at 0.7 m in this case.
The model successfully captured the seasonal variations in water temperature and salinity profiles as well as the stratification across the entire Baltic Sea. In the present study, we show only some typical results for a few stations. Figures 6a-6d show the combined temperature and salinity profiles at the monitoring stations F3, GF, By15, and By5. The profiles are for the complete seasonal cycle showing both the thermal and salinity stratifications. They show good agreements with the field data, although the model values at GF (Gulf of Finland) show less agreement. Table 1 summarizes the absolute and the mean relative errors at the monitoring stations F3, GF, By15, and By5. The last column in Table 1 refers to the difference between simulated and measured values normalized with the measured values. It gives the mean values for the entire 12 months simulation for each station. The model predictions of salinity are better than those of temperature. The maximum errors are in the Bay of Bothnia and Gulf of Finland. The range of the error is 4-10%, which is acceptable considering the large volume of the Baltic Sea and its complex hydrodynamics. Figure 6e compares the modelled and measured water levels at station Visby. There is a good agreement between the two sets of data with a maximum relative error of 10%.
| Absolute error | Mean Relative error % | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time | 14/01/2000 | 28/05/2000 | 18/08/2000 | 09/11/2000 | ||||||
| Station | T (oC) | S (ppt) | T (oC) | S (ppt) | T (oC) | S (ppt) | T(oC) | S (ppt) | T(oC) | S (ppt) |
| F3 | 0.15-0.6 | 0.1-0.2 | 0.1-1.5 | 0.1-0.2 | 0.1-0.2 | 0.1-0.2 | 0.1-0.2 | 0.1-0.2 | 10 | 3 |
| Time | 14/01/2000 | 28/05/2000 | 22/08/2000 | 25/10/2000 | ||||||
| By15 | 0.1-0.57 | 0.1-0.8 | 0.1-1.3 | 0.1-0.8 | 0.1-0.9 | 0.1-0.7 | 0.1-1.6 | 0.1-1.2 | 4 | 4 |
| Time | 14/01/2000 | 28/05/2000 | 22/08/2000 | 25/10/2000 | ||||||
| By5 | 0.1-0.2 | 0.1-0.2 | 0.1-0.5 | 0.1-0.3 | 0.1-0.5 | 0.1-0.3 | 0.1-1.6 | 0.1-2 | 5 | 6 |
| Time | 02/01/200 | 06/06/2000 | - | |||||||
| GF | 0.1-1 | 0.1-0.7 | 0.1-1 | 0.1-0.2 | 9 | 8 | ||||
Table 1: Error summary for temperature and salinity.
Model validation was done for the complete 10 years using the restart files created by the calibration simulation for year 2000. For this purpose, the complete sets of field data at all the monitoring stations were used. These data were considered independently from the simulation results as only the first day records were used in the calibration simulations.
The model predictions of water temperatures and salinities, volumetric exchange rates with the North Sea were satisfactory at all the monitoring stations. This is a significant result as good agreements in the Bay of Bothnia are difficult to achieve due to the sensitive balance between the high inflow of freshwater and the positive salinity gradient from south to north. Here, we choose to show some representative results only for a few stations. The time history plots in Figure 7a compare the model predicted temperature and salinity with the data at stations F3 and By29. The time history plots in Figure 7a compare the model predicted temperature and salinity with the data at stations F3 and By29, which is located in the Northern Gotland Basin.
The time history plots in Figure 7b compare the model predicted salinity with the data at stations BY15 and By5, which are located in the Eastern Gotland Basin and the Bornholm Basin, respectively. The comparisons are shown at the water surface and at deepest points in the basins. The agreements for these stations are better than the other stations as they are closer to the station By1 that defines the model boundary condition. The comparison also shows the ability of the validated model in capturing the large intrusion of the salt from the North Sea that took place on January 18, 2003 (see the lower plot in Figure 7b at station By5). The signature of this salt intrusion is also noticeable at station By5 (Figure 7b the second plot from top).
The range of errors for 4 stations is given in Table 1. The range of Nash-Sutcliffe 18 coefficients calculated for all the monitoring stations were 0.72-0.83, respectively, also suggesting close agreement. One other important feature is the ability of the model to capture the 10-year seasonal variations of water temperatures and salinities. The conclusion is that the model is reasonably validated over a considerable period with a maximum relative error of 10%.
The exchange rates with the North Sea (Table 2) are comparable to the values obtained by Omstedt and Nohr [46]. For the period 1979- 2002, they report mean inflow and outflow rates as 4.275 × 104 m3/s and 5.941 × 104 m3/s. The reported values are well within our results. Our mean inflow and outflow values for the period 2000–09 are 4.955 × 104 m3/s and 4.799 × 104 m3/s, respectively. The lower mean value of outflow is because in our results evaporation losses are already included. We found the mean storage to be +0.15 × 103 m3/s which agrees well with the value +0.11 × 103 m3/s reported by Omstedt and Nohr [47]. Their mean storage values for 2000 and 2001 are 1.06 × 103 m3/s and 3.69 × 103 m3/s respectively, which agree well with the values given in Table 2.
| Year | Inflow (104 m3/s) | Outflow (104 m3/s) | Storage (103 m3/s) |
|---|---|---|---|
| 2000 | 5.026 | 4.816 | 2.100 |
| 2001 | 4.462 | 4.110 | 3.516 |
| 2002 | 4.562 | 4.733 | -1.704 |
| 2003 | 4.597 | 4.800 | -2.028 |
| 2004 | 5.266 | 4.268 | 9.972 |
| 2005 | 5.978 | 5.728 | 2.508 |
| 2006 | 3.754 | 4.216 | -4.620 |
| 2007 | 5.284 | 5.180 | 0.648 |
| 2008 | 5.842 | 5.304 | 5.376 |
| 2009 | 4.780 | 4.835 | -5.520 |
Table 2: Mean volumetric exchange North Sea (Model open boundary at 54028` N 12050´ E and 55022` N 13003).
To quantify tracer transport and exchange between basins of the Baltic Sea, we simulated tracer particle pathways released within twelve basins (Table 3) and from eleven major rivers (Table 4), for the period 2000-2009; the particles are “passive tracers” that do not dynamically affect the ambient water (Appendix). To determine the “optimal” numbers and durations of the particles released from the basins, several different runs were made using a wide range of particle numbers and release durations (numbers: 100, 500, 1000, and 5000; durations: 12 days, 30 days, 1 year, and 10 years). The particle released depths for the basins are listed in Table 3 as well as the maximum and mean basin depths. Figures S1.a-S1.e of the Electronic Supplementary Material (ESM) compare five different simulations cases for the Bay of Bothnia. The plots show the final particle locations and the corresponding depths by the end of 10-years simulation period. The results were consistent however the particle paths and concentrations were found to depend more on the duration than on the number of particles. Increasing the number of the particles increased the absolute, not the relative concentrations. Based on this analysis, we chose to use 1000 particles released over the entire 10-years at locations within basins. We ran different simulations for the rivers by varying both the duration (30 days and 10 years) and the released number of the particles (i.e., 100, 250, and 500, and 1000). We found the spreading of the particles to depend more on the number of particles than on the release duration. Figure S1.g (ESM) compares the two cases of particles released from River Torne in the Bay of Bothnia during 30 days (i.e., January, 2000) and 10-years. Regarding the particle paths, the results were very similar for cases of 500 and 1000 particles. Based on the analysis, we chose 500 particles released over 30 days (January, 2000). Accidental release of contaminated materials in a river is normally of short duration, on the order of days rather than years. Thus, we believe 30 days is an acceptable time scale. It should be noted that the particles were released from the grid cells closest to the shorelines within a depth range of 5-10 m.
| Basin particle released | Particle released depth (m) | Basin maximum depth (m) | Basin mean depth (m) |
|---|---|---|---|
| 1: Bay of Bothnia (BOB) | 76 | 100 | 60 |
| 2: Sea of Bothnia (SOB) | 94 | 195 | 68 |
| 3: Archipelago Sea (AS) | 36 | 95 | 25 |
| 4: Åland Sea (ÅS) | 28 | 50 | 20 |
| 5: Gulf of Finland (GOF) | 52 | 75 | 38 |
| 6: Gulf of Riga (GOR) | 40 | 67 | 29 |
| 7: Northern Gotland Basin (NGB) | 106 | 168 | 77 |
| 8: Western Gotland Basin (WGB) | 100 | 227 | 70 |
| 9: Eastern Gotland Basin (EGB) | 124 | 235 | 90 |
| 10: Bay of Gdansk (BOG) | 88 | 120 | 50 |
| 11: Bornholm Basin (BB) | 82 | 88 | 55 |
| 12: Arkona Basin (AB) | 16 | 40 | 12 |
Table 3: Particle release locations and depths for the Baltic Sea basins.
| River | Country and basin location | Discharge (m3/s) | |||
|---|---|---|---|---|---|
| Mean | Max. | Min | SD | ||
| Kemijoki | Finland (Bay of Bothnia) | 531 | 3770 | 78 | 416 |
| Torne | Sweden (Bay of Bothnia) | 428 | 2990 | 59 | 450 |
| Kalix | Sweden (Bay of Bothnia) | 305 | 1874 | 25 | 305 |
| Lule | Sweden (Bay of Bothnia) | 531 | 1188 | 180 | 168 |
| Neva | Russia (Gulf of Finland) | 2500 | 4180 | 783 | 680 |
| Narva | Estonia (Gulf of Finland) | 400 | N/A | N/A | N/A |
| Daugava | Latvia (Gulf of Riga) | 675 | 2630 | 84 | 445 |
| Venta | Latvia (Eastern Gotland Basin) | 44 | NA | Na | NA |
| Neman | Lithuania (Eastern Gotland Basin) | 616 | 3310 | 174 | 363 |
| Vistula | Poland (Bay of Gdansk) | 1080 | 4390 | 254 | 595 |
| Oder | Poland | 575 | 1416 | 254 | 45 |
Table 4: Flow discharges for rivers used in particle tracking simulations.
The arrival time is computed as the time taken for the first particles to cross the “boundaries” of each basin (Figure 2). Similarly the time of arrival at a shoreline is the time taken for the first particles to cross the closest grid cell to the shoreline. Relative particle concentrations are defined within each basin (water body) volume as the ratio of the particle numbers at a given time, divided by the total number of initially released particles from a given location up to the end of 2009.
To facilitate the ease of reading some of the simulations results are moved into the Electronic Supplementary Material (ESM) which is noted by the letter S. The results included in ESM are:
• Figures S1.a-S1.f: Comparison of Particle release duration and particle numbers for the Bay of Bothnia and River Torne. Particles depths are shown by the colour scale.
• Figures S2.a-S2.l: Particle tracking in the major basins of the Baltic Sea in the period 2000-2009. Particles depths are shown by the colour scale. The dark grey colour shows the paths covered by the particles.
• Figures S3.a-S3.j: Particle tracking for the major rivers of the Baltic Sea. Particles 8 depths are shown by the colour scale.
The hydrodynamic characteristics of the Baltic Sea were comprehensively explored using the validated model for the period 2000-2009. The study addressed in details, the thermal and salinity stratifications, the volumetric water exchange rates, and the vortical structures in addition to the particle tracking. Various parameters were also computed basin wise such as Rossby deformation radius, Ekman layer thickness, and Görtler number [48]. In the following, we first present a short summary of the two key features i.e. stratification and the vortical structures and illustrate a few typical features in Figures 8a-8e, Figure 8b shows the thermal stratification on May 12, 2000 for a section (i.e., S116, Figure 8a) for section that crosses the Northern Gotland Basin and the Sea of Bothnia in west-east direction. An example of the salinity stratification for the same cross-section S116 is shown in Figure 8c on May 12, 2000. Figure 8d shows the velocity vectors and the interpolated vortical structures in the Sea of Bothnia on May 12, 2000. Figure 8d shows the surface velocity vectors in the Gulf of Finland on March 29, 2000 and the large scale vortices.
Stratification
The study addressed both the thermal and salinity stratifications with the focus on the structural properties of the layers. The detailed investigation of thermal stratification for a 10-year period (i.e., 2000– 2009) revealed some new features. A multi-layered structure that contains several thermocline and dicothermal layers prevails (Figure 8b). We have found the three-layer model cited in the literature [24] to be valid only during the winter periods. Following the winter period, however, the three-layered structure is decomposed into several layers (up to 5). This process takes place in all of the basins. The layering properties vary significantly among the basins whereby the layered structure could not be entirely generalized. Nevertheless, a few generalizations appear to be possible. The thermocline occupies about 25% of the water depths in each basin. The deep bottom layer is about 40% of the water depth with temperatures of about 3°C, and 5°C in northern and southern basins, respectively. The good correlation between water and air temperatures suggests the thermocline dependency on the atmospheric forcing fluctuations.
We found some evidence of upwelling and downwelling along the coastlines of the northern basins of the Baltic Sea during the simulation period. The two features occur as wind causes surface water to diverge (Ekman transport) or converge (downwelling). During both processes, either water is replaced from the deep region or is forced downwards. A phenomenon which is indicative and closely related to the upwelling and downwelling processes is dicothermal. It is characterised by relatively high gradients of salinity and density. An example is given in Figure 8b that clearly shows the existence of a cold water region (dicothermal) sandwiched between warmer layers in the Gulf of Finland.
Three-layered salinity stratification prevails in all basins of the Baltic Sea in general agreement with the previous studies (Figure 8c) [24]. Salinity stratification has a seasonal variability but much weaker than the corresponding variability in temperature. We have succeeded to generalize the seasonal normalized layer thicknesses with the flow depth for the entire 10-year period. Typically, the layer thickness is in the range of 18-50%, 15-66%, and 12-50% in the upper, middle, and bottom layers, respectively, with significant seasonal variations in all basins.
Vortical structures
The transport characteristics that derive the various mixing and exchange processes in the Baltic Sea could be understood in terms of the vortical structures. The details of these large scale organized vortices both in horizontal and vertical planes are given by Dargahi and Cvetkovic [48]. Here, a short summary is presented.
In the horizontal plane, vortices with typical length and velocity scales of 5-12 km and 5-10 cm/s, are present (Figure 8e). We found the scales to be comparable to the mean baroclinic Ross by deformation radius of 5km. These vortices are of open type three-dimensional structures having two important features. They extend to 90% of the flow depth and have a clear periodicity of one to seven days. The vortices rotate both in clockwise and anti-clockwise directions.
In the vertical planes, there is a multi-layered structure with the layer numbers varying from 2 to 4. Each layer is characterized by a set of distinct vortices. Different transport modes prevail due to the frequent reversal of the velocity directions in the upper and lower layers and the induced shear layer instabilities, lead to. Taylor- Görtler type vortices appear within the surface layers (Figure 8d). The middle flow layers are featured by distorted large-scale vortices.
Boundary trapped vortices and large local circulation patterns feature the deeper bottom flow layers. The topography of the basins creates a general circulation pattern that is either clockwise or anticlockwise depending on the flow direction in the surface layer. The downwelling and upwelling flow phenomena are controlled by the vortices at least in the vertical planes.
Here we present a short and compact description of the particle paths in the various basins of the Baltic Sea. The Electronic Supporting Material (ESM) that contains the full particle path descriptions and the corresponding figures. The particles paths in rivers as well the figures are only described in the ESI. The descriptions in the basins are accompanied by Figures 9a-9j and S2.a-S2.n, S refers to the ESI.
Bay of Bothnia, the general mixing and particle migration characteristics are a large -scale anti-clockwise rotation of the deep and mid-depth layers. The general path is through Northern Quark enter the Sea of Bothnia.
Sea of Bothnia the main particle paths are northwards within the basin and a limited southwards migration out of the basin (Figure 9b the 3D and histogram plots). Some particles pass through Kumlinge Sill and then enter the Archipelago Sea after.
Åland Sea, the particles split into two main north and southwards directions. The general paths are northwards passing Archipelago Sea and the Sea of Bothnia (Figure 9c the 3D and histogram plots).
Archipelago Sea, the particles initially split at the release location, into three different northwest, southwest, and east directions. However, the principal particle paths are northwest and southeast. Figure 9d shows a typical path for one particle moving north-westwards and the corresponding particle distributions with depth.
Gulf of Finland, particles remain stationary for 30 days within the released point and thereafter migrate towards the northern and southern shorelines at a speed of 2.5 cm/s. Figure 9e shows a typical path for one particle moving north-westwards and the corresponding particle distributions with depth.
Northern Gotland Basin, particles remain stationary within a narrow radius of 20 km for 90 days, and then start to spread in all four directions (NW-SW-SE-E) at a relatively high mean speed of 6 cm/s. Figure 9f shows a typical path for one particle and the corresponding particle distributions with depth. Particles pass through the Åland Sill and enter the Åland Sea and the Archipelago Sea.
Western Gotland Basin the particles spread into north and southwards directions covering most of the basins of the Baltic Sea. Figure 9g shows a typical path for one particle migrating north-westwards.
Eastern Gotland Basin, the general particle paths are similar to those in the Western Gotland Basin that is northwards and southwards directions. Figure 9h shows a typical path for one particle migrating north-westwards and the corresponding particle distributions with depth.
Bornholm Basin, the general particle paths follow two main north-eastwards north-westwards directions. Figure 9i shows a typical path for one particle migrating north-westwards and the corresponding particle distributions with depth.
Arkona Basin, the particles follow two different paths in the anti-clockwise circulation that crosses most of the lower basins of Baltic Sea around the Gotland Island and a north westwards path that reaches the Bay of Bothnia. Figure 9j shows a typical path for one particle migrating northwards.
The key features of tracer transport in the Baltic Sea basins during 2000-2009 are given in Tables 5.1-5.9, as first arrival times and mass fraction at the end of 2009. Since the boundaries between basins may be considered as a “transition zone”, i.e., they are not exact positions in view of the irregular shoreline and presence of archipelagos, the first arrival times are given with a 5-day accuracy. The full description of the transport that provides details of principal features of particle movement over the 10-year period is given in ESM where basins and rivers are considered separately. Tables 6.1-6.6 summarize the tracer transport features for particles released from 9 major rivers as listed by Table 3. The two rivers Kalix and Kemijoki had similar tracer transport characteristics and are not summaries in Tables 6.1-6.7.
| Release depth (m) | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Bay of Bothnia 76 m | Bay of Bothnia | - | 90 |
| Sweden shoreline | 90 | - | |
| Finish shoreline | 210 | - | |
| Northern Quark | 515 | - | |
| Sea of Bothnia | 1860 | 10 | |
| Sea of Bothnia 94 m | Sea of Bothnia | - | 80 |
| Sweden shoreline | 182 | - | |
| Finish shoreline | 280 | - | |
| Southern Quark | 586 | - | |
| Åland Sea | 673 | 4 | |
| Archipelago Sea | 761 | ||
| Gotland Sandö Sill | 971 | - | |
| Northern Gotland Basin | 1016 | 1 | |
| Bay of Bothnia | 1117 | 15 | |
| Eastern Gotland Basin | 1756 | - | |
| Gulf of Riga | 1756 | - | |
| Western Gotland Basin | 1874 | - | |
| Gulf of Finland | 2015 | - | |
| Bay of Gdansk | 3409 | - |
Table 5.1: Summary results of the particle tracking in the Bay and Sea of Bothnia. The mean Lagrangian velocity is 2-4.5 cm/s in the Bay of Bothnia and 3-5 cm/s in the Sea of Bothnia. The advection-diffusion ratio for both basins is χ=1.
| Release depth (m) | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 28 m | Archipelago Sea | 90 | - |
| Sea of Bothnia | 100 | 75 | |
| Northern Gotland Basin | 124 | 7 | |
| Western Gotland Basin | 540 | 5 | |
| Gulf of Finland | 900 | 2 | |
| Northern Quark | 900 | ||
| Bay of Bothnia | 1200 | 10 | |
| Eastern Gotland Basin | 1260 | 1 |
Table 5.2: Summary results of the particle tracking in the Åland Sea. The mean Lagrangian velocity is 3-5 cm/s. The advection-diffusion ratio for both basins is χ=1.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 36 m | Western Gotland Basin | 116 | 5 |
| Gulf of Finland | 164 | 35 | |
| Åland Sill | 324 | - | |
| Northern Gotland Basin | 340 | 15 | |
| Kumlinge Sill | 499 | - | |
| Åland Sea | 639 | - | |
| Sea of Bothnia | 720 | 35 | |
| Eastern Gotland Basin | 730 | 5 | |
| Bornholm Sea | 1508 | - | |
| Arkona Basin | 1915 | - | |
| Bay of Bothnia | 2190 | 5 | |
| Gulf of Riga | 2190 | - |
Table 5.3: Summary results of the particle tracking in the Archipelago Sea. The mean Lagrangian velocity is 3-5 cm/s. The advection-diffusion ratio for both basins is χ=1.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 52 m | Gulf of Finland | - | 70 |
| Gulf of Finland Southern shoreline | 180 | - | |
| Northern Gotland Basin | 180 | 15 | |
| Archipelago Sea | 345 | 3 | |
| Sweden shoreline | 485 | - | |
| Åland Sea | 665 | 2 | |
| Eastern Gotland Basin | 1080 | 5 | |
| Sea of Bothnia | 1240 | 4 | |
| Western Gotland Basin | 1350 | 1 |
Table 5.4: Summary results of the particle tracking in the Gulf of Finland. The mean Lagrangian velocity is 2-4 cm/s. The advection-diffusion ratio for both basins is χ=0.46.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 106 m | NG Basin | - | 36 |
| Åland Sea | 180 | - | |
| Gulf of Finland | 309 | 10 | |
| Eastern Gotland Basin | 430 | 6 | |
| Western Gotland Basin | 565 | 5 | |
| Archipelago Sea | 700 | - | |
| Stockholm shoreline | 900 | - | |
| Sea of Bothnia | 910 | 40 | |
| Northern Quark | 1227 | - | |
| Bornholm Basin | 1730 | - | |
| Bay of Bothnia | 2155 | 2 | |
| Bay of Gdansk | 2155 | - | |
| Arkona Basin | 2460 | 1 |
Table 5.5: Summary results of the particle tracking in the Northern Gotland Basin. The mean Lagrangian velocity is 3-15 cm/s. The advection-diffusion ratio for both basins is χ=30.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 100 m | WG Basin | - | 10 |
| Gotska Sandö Sill | 77 | - | |
| Northern Gotland | 136 | 30 | |
| Stockholm shoreline | 136 | - | |
| Åland Sea | 253 | - | |
| Archipelago Sea | 515 | - | |
| Sea of Bothnia | 575 | 40 | |
| Gulf of Finland | 760 | 10 | |
| Eastern Gotland | 850 | 8 | |
| Bornholm Basin | 1395 | 2 | |
| Arkona Basin | 1550 | - | |
| Bay of Gdansk | 1982 | - | |
| Bay of Bothnia | 2939 | - |
Table 5.6: Summary results of the particle tracking in the Western Gotland Basin. The mean Lagrangian velocity is 5-10 cm/s. The advection-diffusion ratio for both basins is χ=250.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 124 m | EG Basin | - | 12 |
| Stockholm shoreline | 175 | - | |
| N. Gotland Basin | 175 | 20 | |
| W. Gotland Basin | 515 | 10 | |
| Åland Sea | 515 | - | |
| N. Gotland | 530 | - | |
| Gulf of Finland | 545 | 20 | |
| E. Gotland Basin | 613 | - | |
| Gulf of Riga | 685 | - | |
| Archipelago Sea | 770 | ||
| Sea of Bothnia | 940 | 28 | |
| Stockholm shorelines | 1075 | 10 | |
| Bay of Gdansk | 2000 | - | |
| Bornholm Basin | 2022 | - | |
| Arkona Basin | 2178 | - | |
| Bay of Bothnia | 2735 | - |
Table 5.7: Summary results of the particle tracking in the Eastern Gotland Basin. The mean Lagrangian velocity is 5-11 cm/s. The advection-diffusion ratio for both basins is χ=110.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 82 m | B Basin | - | 25 |
| Eastern Gotland Basin | 188 | 10 | |
| Fårö Sill | 304 | - | |
| Arkona Basin | 304 | 5 | |
| Bay of Gdansk | 410 | - | |
| Western Gotland Basin | 545 | 15 | |
| Northern Gotland Basin | 545 | 15 | |
| Åland Sea | 720 | 2 | |
| Gulf of Finland | 1095 | 5 | |
| Archipelago Sea | 1472 | 3 | |
| Sea of Bothnia | 1610 | 20 | |
| Bay of Bothnia | 2526 | - |
Table 5.8: Summary results of the particle tracking in the Bornholm Basin. The mean Lagrangian velocity is 5-10 cm/s. The advection-diffusion ratio for both basins is χ=60.
| Release depth | Basins/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| 16 m | A Basin | - | 3 |
| Hamrare Strait | 137 | - | |
| Stople Channel | 165 | - | |
| Bornholm Sea | 170 | 22 | |
| Eastern Gotland Basin | 210 | 10 | |
| Northern Gotland Basin | 849 | 10 | |
| Western Gotland Basin | 883 | 10 | |
| Åland Sea | 1185 | 40 | |
| Archipelago Sea | 1295 | ||
| Sea of Bothnia | 1373 | ||
| Bay of Bothnia | 1988 | - | |
| Gulf of Finland | 2095 | 5 |
Table 5.9: Summary results of the particle tracking in the Arkona Basin. The mean Lagrangian velocity is 5-10 cm/s. The advection- diffusion ratio for both basins is χ=60.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Kemijoki | Bay of Bothnia | 68 | 98 |
| Northern Quark | 1235 | - | |
| Sweden NE shoreline | 1835 | - | |
| Sea of Bothnia | 1835 | 2 | |
| Torne | Northern shoreline -Bay Bothnia | 888 | 99 |
| Northern Quark | 930 | - | |
| Sea of Bothnia | 2158 | 1 | |
| Kumlinge & Åland Sills | 3555 | - | |
| Kalix | Northern shoreline -Bay Bothnia | 300 | 99 |
| Deep region - Bay Bothnia | 2070 | - | |
| Lule | Bay of Bothnia | 63 | 99 |
| Northern Quark | 742 | - | |
| Sea of Bothnia | 1515 | 1 | |
| Sweden northeast shoreline | 1825 | - | |
| Southern Quark | 2555 | - | |
| Kumlinge Sill | 2810 | - |
Table 6.1: Summary results of the particle tracking from rivers Kemijoki, Torne, Kalix and Lule discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Neva | Exiting Gulf of Finland | 730 | 60 |
| Northern Gotland Basin | 912 | 10 | |
| Åland Sea | 1168 | 4 | |
| Archipelago Sea | 1293 | ||
| Sea of Bothnia | 1468 | 10 | |
| Eastern Gotland Basin | 1537 | 10 | |
| Western Gotland Basin | 1840 | 5 | |
| Shorelines of Latvia | 1963 | - | |
| Bay of Gdansk | 2502 | - | |
| Bornholm Basin | 2798 | 1 | |
| Arkona Basin | 2798 | - |
Table 6.2: Summary results of the particle tracking from river Neva discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Narva | Gulf of Finland | 30 | 55 |
| Öland northern shoreline | 757 | - | |
| Northern Gotland Basin | 912 | 15 | |
| Åland Sea | 1128 | - | |
| Archipelago Sea | 1293 | 5 | |
| Gotska Sandö Sill | 1440 | - | |
| Western Gotland Basin | 1817 | 8 | |
| Eastern Gotland Basin | 2385 | 1 | |
| Bornholm Basin | 2413 | 5 | |
| Bay of Bothnia | 2499 | - | |
| Sea of Bothnia | 2904 | 11 | |
| Bay of Gdansk | 2985 | - |
Table 6.3: Summary results of the particle tracking from river Narva discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Daugava | Exit Gulf of Riga | 400 | 65 |
| Eastern Gotland Basin | 640 | 10 | |
| Western Gotland Basin | 863 | 10 | |
| Gotska Sandö Sill | 640 | - | |
| Northern Gotland Basin | 1390 | - | |
| Bornholm Basin | 1390 | 3 | |
| Öland eastern shorelines | 1470 | 6 | |
| Bay of Gdansk | 1730 | - | |
| Åland Sea & Stockholm shorelines | 1915 | 1 | |
| Arkona Basin | 1915 | - | |
| Åland Sea | 2310 | 2 | |
| Sea of Bothnia | 2499 | 3 |
Table 6.4: Summary results of the particle tracking from river Daugava discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Venta | Saaremaa Island | 23 | - |
| Gulf of Riga | 640 | - | |
| Eastern Gotland Basin | 30 | 25 | |
| Western Gotland Basin | 640 | 25 | |
| Northern Gotland Basin | 890 | 10 | |
| Bornholm Basin | 935 | 10 | |
| Archipelago Sea | 1300 | - | |
| Åland Sea | 1300 | 24 | |
| Sea of Bothnia | 1350 | ||
| Arkona Basin | 1480 | 4 | |
| Gulf of Finland | 1760 | 2 | |
| Bay of Gdansk | 1844 | - |
Table 6.5: Summary results of the particle tracking from river Venta discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Neman | Bay of Gdansk | 167 | 15 |
| Bornholm Basin | 180 | 11 | |
| Eastern Gotland Basin | 300 | 15 | |
| Arkona Basin | 925 | 3 | |
| Öland eastern shoreline | 1045 | 5 | |
| Northern Gotland Basin | 1045 | 5 | |
| Gotland northern shorelines | 1045 | 5 | |
| Gulf of Finland | 1123 | 3 | |
| Stockholm shorelines | 1264 | 3 | |
| Western Gotland Basin | 1380 | 25 | |
| Åland Sea | 1450 | 10 | |
| Sea of Bothnia | 1550 |
Table 6.6: Summary results of the particle tracking from river Neman discharging into the Baltic Sea.
| River | Basin/Shoreline | Arrival time (days) | Particle concentration (%) |
|---|---|---|---|
| Vistula | Eastern Gotland Basin | 240 | 10 |
| Bornholm Basin | 240 | 25 | |
| Arkona Basin | 358 | 5 | |
| Sweden southeast shorelines | 395 | 5 | |
| Northern Gotland Basin | 745 | 15 | |
| Western Gotland Basin | 870 | 30 | |
| Archipelago Sea islands | 1147 | - | |
| Gulf of Finland | 1365 | 2 | |
| Åland Sea | 1760 | 13 | |
| Sea of Bothnia | 1795 | ||
| Bay of Bothnia | 2500 | - | |
| Oder | Arkona Basin | 50 | 5 |
| Bornholm Basin | 150 | 10 | |
| Stople channel | 218 | - | |
| Eastern Gotland Basin | 240 | 10 | |
| Sweden southeast shorelines | 350 | 30 | |
| Western Gotland Basin | 730 | 25 | |
| Northern Gotland Basin | 790 | 10 | |
| Åland Sill | 919 | 6 | |
| Åland Sea | 1221 | ||
| Archipelago Sea | 1275 | - | |
| Sea of Bothnia | 1335 | 4 |
Table 6.7: Summary results of the particle tracking from rivers Vistula and Oder discharging into the Baltic Sea.
Accompanying Tables 5 and 6 are Figures 9 and 10 for the basins and rivers, respectively. Figures 9 and 10 provide three key features of particle transport: i) A typical pathway developed over the 10 year simulation period (2D); ii) the same particle pathway in three-dimensions where one can follow the vertical transition; iii) a histogram of the same particle of the visited depths over the 10-year simulation period irrespective of the horizontal position. Figures 9 and 10 are complemented with Figures S2-S3 of the ESM. We also present in the ESM the complete set of plots for all the basins and the major rivers. They show the final locations of the particles in each basin and the corresponding depths.
The general observed feature of the pathways illustrated in Figures 9 is that a particle released in a basin at the lower half depth will ultimately spend significant time at shallower depths, i.e., within the upper half depth; this is particularly true for northern basins, Figures 9a-9e. i.e., from the Northern Gotland Basin (Figure 9f) to the Arkona Basin (Figure 9j) a bimodal feature of the depth distribution that follows the stratification is clearly observable. Interestingly, the bimodal feature of the depth distribution is not observed for particles released in rivers close to the surface, where for almost all rivers particles will have a tendency to remain in the upper half of the depth. The pathways illustrated in Figures 9 and 10a-10k suggests a random walk type of transitions. One way of describing such transitions is by the distribution of displacement (segment) lengths at fixed time intervals, and the associated velocities. The segment length and associated velocity histograms for a typical particle pathway released from Bay of Bothnia (Figure 9a) are shown in Figures 11a and 11b, respectively. The most dominant segment length is around 2km with a dominant velocity in 8 the range 1-2 cm/s. A detailed random walk analysis would consider all three components of the displacement and velocity vectors.
Tables 5 and 6 combined with Figures S9 and S10 contain the main particle transport results, in terms of first arrival and the spatial distribution. Considering the relatively many source locations for basins and rivers, and the fact that particles typically exhibit complex pathways in view of the vortical characteristics of the Baltic Sea flow, providing a full and comprehensible description of the transport in space and time for all sources and particles posed a significant challenge. The ESM provides detailed yet concise histories of particle transport from the different sources, with an attempt to systemise predominant transport directions and locations both horizontally and with depth, as these evolve over the 10-year simulation period. This provides the basis for understanding main global and regional features of Baltic Sea transport from multiple-source locations.
Based on the information in Tables 5 and 6, we propose in the following a few compact measures of exchange processes between the major basins of the Baltic Sea, as one means of quantifying inter-basin exchange (mass fraction) and deliveries (mass fraction per unit time).
Inter-basin exchange
Let βij denote the mass fraction that is exchanged between basin i and basin j of major basins of the Baltic Sea; the computed values of βij are summarised in Table 7.1 (index i signifies rows and index j signifies columns). For instance, the fraction of particles released in the Gulf of Finland (i=GoF) at 2000 that are still in the Gulf of Finland (j=GoF) at the end of 2009, is 70% (Table 7.1), whereas only 9% of the particles released in the Gulf of Finland has been delivered e.g., to the Sea of Bothnia at the end of 2009 (i=GoF, j=SoB, Table 7.1). Using βij, we define an exchange index for each basin as
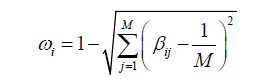 (1)
(1)
| BoB | SoB | GoF | WG | NG | EG | BB | ω | |
|---|---|---|---|---|---|---|---|---|
| Bay of Bothina (BoB) | 0.9 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0.11 |
| Sea of Bothnia (SoB) | 0.15 | 0.84 | 0 | 0 | 0.01 | 0 | 0 | 0.17 |
| Gulf of Finland GoF) | 0 | 0.09 | 0.7 | 0.01 | 0.15 | 0.05 | 0 | 0.33 |
| Western Gotland (WG) | 0 | 0.4 | 0.1 | 0.1 | 0.3 | 0.08 | 0.02 | 0.63 |
| Northern Gotland (NG) | 0.02 | 0.4 | 0.1 | 0.05 | 0.36 | 0.06 | 0.01 | 0.57 |
| Eastern Gotland (EG) | 0 | 0.28 | 0.2 | 0.1 | 0.3 | 0.12 | 0 | 0.7 |
| Bornholm Basin (BB) | 0 | 0.25 | 0.05 | 0.15 | 0.15 | 0.1 | 0.3 | 0.72 |
Table 7.1: Distribution of particle fractions across major basins at end of 2009; rows signify the basin of particle release in 2000.
in which we choose M=7, i.e., we have aggregate some of the 12 minor basins into larger ones. Specifically, Archipelago Sea and Åland Sea are both considered to be part of Sea of Bothnia 5 (Figure 2), Gulf of Riga is considered as part of Eastern Gotland Basin (Figure 2), and Bay of Gdansk 6 and Arkona Basin are both considered as part of the Bornholm Basin (Figure 2). If the mass injected in basin i is distributed evenly in all M=7 major basins (whereby basin i would be a perfect global 8 “diffusor”), ωi would be 1; for increasing M and more concentrated (or less evenly distributed) mass, ωi converges to zero.
In Table 7.1 we show ω for each of the 7 major basins. It is seen that BoB has the lowest ω, and BB the highest, which is consistent with the fact that 90% of particles injected into BoB stay there from 2000 to 2009, whereas those injected in BB are rather evenly distributed throughout the basins. Roughly, the 7 basins can be divided into three categories based on the computed value of ω: low (BoB and SoB), intermediate (GoF), and high (WG, NG, EG and BB). The basin of the peak fraction is for the first three basins located in the basin of origin, whereas for the last 4 it lies elsewhere, BB being the exception with a nevertheless high ω. Thus ω is a simple indicator for understanding mass exchange between basins.
Next, we summarise in Table 7.2 the mass fractions of exports from the 11 major rivers. Let ρij denote the mass fraction of exports from the 11 major rivers (index i=1,N; N=11) to the major selected basins (index j=1,M, M=7); the computed values of ρij are summarised in Table 7.2 (index i signifies rows and index j signifies columns). For instance, the fraction of mass discharged by river Neva (i=Neva GoF) at 2000 that is still in the Gulf of Finland (j=GoF) at the end of 2009, is 60% (Table 6.2), whereas 14% of the mass discharged by Neva into the Gulf of Finland has been delivered to the Sea of Bothnia at the end of 2009 (i=Neva GoF, j=SoB, Table 6.2).
| BoB | SoB | GoF | WG | NG | EG | BB | θ | |
|---|---|---|---|---|---|---|---|---|
| Torne (BoB) | 0.99 | 0.01 | 0 | 0 | 0 | 0 | 0 | 0.009 |
| Kalix (BoB) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lule (BoB) | 0.99 | 0.01 | 0 | 0 | 0 | 0 | 0 | 0.009 |
| Kemijoki (BoB) | 0.98 | 0.02 | 0 | 0 | 0 | 0 | 0 | 0.018 |
| Neva (GoF) | 0 | 0.14 | 0.6 | 0.05 | 0.1 | 0.1 | 0.01 | 0.124 |
| Narva (GoF) | 0 | 0.16 | 0.55 | 0.08 | 0.15 | 0.01 | 0.05 | 0.153 |
| Daugava (EG/BOR) | 0 | 0.06 | 0 | 0.1 | 0 | 0.75 | 0.09 | 0.106 |
| Venta (EG) | 0 | 0.24 | 0.02 | 0.25 | 0.1 | 0.25 | 0.14 | 0.237 |
| Neman (EG) | 0 | 0.1 | 0.03 | 0.3 | 0.08 | 0.15 | 0.34 | 0.32 |
| Vistula (BB) | 0 | 0.13 | 0.02 | 0.3 | 0.15 | 0.1 | 0.3 | 0.241 |
| Oder (BB) | 0 | 0.1 | 0 | 0.25 | 0.1 | 0.1 | 0.45 | 0.205 |
Table 7.2: Fraction of particles released from major rivers in 2000 that end up in major basins 2009. The rivers are divided in roughly three categories depending on the value of θ.
Using ρij we define a “transfer index” in an analogous manner as ω:
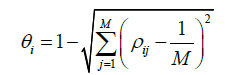 (2)
(2)
Higher value of θi indicates that the river i transfers, or disperses mass over a wider range of basins, whereas lower θi indicates the opposite, i.e., a relatively low dispersion of mass from river i within the selected major basins. From the last column in Table 7.2, we see that the 11 rivers fall roughly into three categories: Torne, Kalix. Lule and Kemijoki with a low θi and hence low 5 transfer to basins other than the one into which the river discharges; Neva, Narva and Daugava with an intermediate value of θi that transfer mass to other basins although the peaks remain in the basins into which the river discharges; and Venta, Neman, Vistula and Oder with a relatively high θi indicating significant and comparatively even mass transfer to most of the basins. Exception is the river Oder with a peak remaining in the basin of origin (BB) that nevertheless yields a relatively high θ (last row of Table 7.2).
The measures of internal mass exchange (ω) and of river-load mass transfer (θ) provide simple indicators of passive particle transport in the Baltic Sea over the period 2000-2009. The number of basins could have been higher or selected differently which would depend on the particular issue at hand; also, the selection of injection points within the basins affects the exact computed values of the indicators θ and ω. In other words, the exact values of θ and ω in Tables 7.1 and 7.2 should be considered only as relative measures to be further refined and explored as part of the transport/exchange characterisation of the Baltic Sea. Furthermore, the release points at the rivers could be expanded to include (or be replaced by) release points from coastal wastewater treatment plants for instance, depending on the application of interest. The corresponding information as that provided in Tables 7.1 and 7.2 can then be used for assessing the potential internal spreading of tracers within the basins of the Baltic Sea.
Skwarzec and Tuszkowska [49] for instance find high concentrations of Polonium Po in the Oder River. Annually the river supplies the Baltic Sea with 14.6 GBq 210Po that will only take 50 days to reach the Arkona Basin and 240 days the Eastern Gotland Basin. It is plausible that other rivers entering the Baltic Sea carry greater or comparable loads of potentially toxic substances. Another issue of current concern is the impact of micro-plastics on the marine ecosyst ems [50]. It has been estimated that a total of between 13-39 tons of micro-plastics are released into the Baltic Sea annually. The main sources are wastewater treatment plants discharging directly along the coast, or indirectly through rivers. Table 7.2 could be complemented to include the major waste water treatments plants wherefrom the distribution of the total micro-plastics load among major basins could be readily computed. Finally, Tables 7.1 and 7.2 provide a means for simple (first) estimates of the nutrient distribution between basins of the Baltic Sea, released internally from sediments or discharged (externally) from rivers.
Inter-basin delivery
Combining the first arrival times and final mass fraction distribution, one can compute an upper bound of the mass delivery [M/T] defined here as mass fraction per unit time [1/T]. We shall illustrate the delivery upper bound only for tracer source in the basins.
By dividing the mass fraction (or relative concentration) in a given basin with the first arrival time to that basin, this upper bound is computed and summarised in Table 8. Once again, it is seen that the Bay and Sea of Bothnia are characterised by (relatively low) delivery only between each other. Moving southward, relatively high delivery is found from the Gulf of Finland to the Northern Gotland Basin, and comparatively small deliveries elsewhere. Western Gotland Basin delivers mass to almost all basins with the highest value (large mass fraction and short fist arrival) found for the neighbouring Northern Gotland Basin. The Northern and Eastern Gotland, and Bornholm Basins deliver tracer mass more evenly to most other basins. The next step could be to carry out a more detailed analysis of how delivery changes over time at sections specified based on a particular transport problem at hand.
| Delivery [1/day] 1E+5 | BoB | SoB | GoF | WG | NG | EG | BB |
|---|---|---|---|---|---|---|---|
| Bay Of Bothina (BoB) | - | 5.4 | 0 | 0 | 0 | 0 | 0 |
| Sea of Bothnia (SoB) | 13.5 | - | 0 | 0 | 1 | 0 | 0 |
| Gulf of Finland GoF) | 0 | 5 | - | 0.74 | 83 | 4.6 | 0 |
| Western Gotland (WG) | 0 | 70 | 13 | - | 222 | 9.4 | 1.4 |
| Northern Gotland (NG) | 0.9 | 44 | 32 | 9 | - | 14 | 0.4 |
| Eastern Gotland (EG) | 0 | 30 | 37 | 20 | 62 | - | 0 |
| Bornholm Basin (BB) | 0 | 12 | 4.5 | 28 | 28 | 52 | - |
Table 8: Mass fraction deliveries from (rows)-to (columns) major basins of the Baltic Sea at the end 2009.
Transport mechanism
The particle tracking results will now be used to discuss some of the basic transport mechanisms and the exchange processes among the basins.
To discuss the particle transport characteristics, we first introduce two new parameters to relate the particle concentration in percentage to the flow properties, i.e. advective (Cad) and diffusive (Cdi) changes in particle concentration:
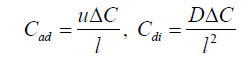 (3)
(3)
in which u=velocity scale, ΔC=change in particle concentration, D=horizontal diffusion coefficient, and=travel length scale. Here, is defined as the averaged length travelled by the particles in unit transport time. The averaged velocity scale for a selected particle was found from the frequency plot of particle velocities (i.e., vectors) integrated in time. For a selected particle the travelled lengths were found by √(xi+1-xi)2 +(yi+1-yi)2 +(zi+1-zi)2 ( i is the time index). Typical values were u=0.02 m/s and l=4.5 km. An example is shown in Figure 11 for just one particle released in the Bay of Bothnia in the period 2000-2009. For the Baltic Sea D=100 m2/s 20 is commonly used [24]. We can form a new ratio by dividing the advective change with the diffusive change to get
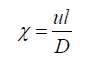 (4)
(4)
It is notable that Eq. (4) is analogous to the Reynolds number (ratio of the inertial force to the viscous force). The proposed ratio or Reynolds number should be understood in terms of the length and velocity scales of the particle displacement.
The particle path results suggest two possible transport mechanisms within the basins and among the basins i.e., barotropic and baroclinic. However, the significant differences in temperature (≈10°C) and salinity (≈24 ppt) between the waters of the North Sea and Baltic Sea imply dominant baroclinic transport as opposed to the barotropic transport through the Danish Straits [24,51]. We found the normalized variances of water level differences between the model open boundary and the Arkona Basin four times lower than the values for temperature and salinity differences.
In ESM we show the complexity of the particle pathways within each Baltic Sea basin, in particular in terms of the various circulation patterns that have strong 3D features (Figures 9 and 10). The upward migration of the particles suggests mixing of the deeper water layers and with the shallower water layers. Here, the main mechanism is baroclinic transport that is related to the strong stratifications in all the basins of the Baltic Sea (Figures 8b and 8c). The circulation is density driven by baroclinic instabilities. Here, the underlying mechanism is shear layer instabilities that are generated by density differences between two adjacent layers. The large scale eddies are formed by these instabilities (Figures 8d and 8e).
The water exchange among the basins primarily takes place through the various sills and channels that connect the Baltic Sea basins (Figure 2). In the description of the tracers we emphasized the importance of these interconnecting channels. However, the channels have much smaller dimensions in comparison with the basins having depths in the range of 5-30 m. The implication is that locally, the transport mode is more advective that is partly driven by the river surface flow contributions and partly by the horizontal pressure gradient across the channels. The latter is driven by the water level differences across the channels with a typical value of ±5 cm [48]. The water layers within these relatively shallow channels have weak stratification due to wind mixing (see the same reference).
Next, we discuss the specific characteristics of each basin. The hydrodynamics of the Bay of Bothnia can be characterised by internal mixing of the water masses within the basin and limited exchange with the Sea of Bothnia as indicated by the high particle concentration of 90% mass fraction after 10-years (Table 5). The Bay of Bothnia is supplied with 75 km3/year of freshwater, which is 18% of the total inflow into the Baltic Sea. This high momentum flow causes shearing of the lower layers by inducing a dynamic shear force that contributes to the internal mixing within the bay. The mixing is controlled by different types of eddies. Section 7.2 illustrated the existence of Taylor- Götter type and large scale vortices (Figure 8d). Omstedt and Nohr [47]; Myrberg and Andrejev [52] also report the process of internal mixing and circulation in the bay. Table 5.1 shows that both advective and diffusive processes control the transport characteristics of the bay.
The Sea of Bothnia exchanges mass mainly with the Bay of Bothnia. The other minor exchanging basins are the Åland Sea, the Archipelago Sea, the Gulf of Finland, and Northern and Western Gotland Basins (Tables 5.2-5.6). Previous studies indicate that the mixing is essentially through the Åland Sea [53]. However, a notable particle transport was found through the shallow islands of the Archipelago Sea. The particle first arrival time to the Archipelago Sea (Table 5.3) is longer than for the Åland Sea. The difference in time could be explained by increased diffusive transport, which is slower than the advective component.
Note that the particle pathways in the northern part of the Sea of Bothnia are comparable to the movement of drifting buoys in the same region Figure 5.10 [24].
Particles released within the shallow islands of the Archipelago Sea were found to cover a large area of the Baltic Sea (Figure S2.c). This is an important result due to the existence of many fish farms and other potentially contaminating activities within this region. The implication is that contaminants will travel by the surface water that has a higher advection velocity than the lower water layers to the sensitive areas in the Baltic Sea, especially the shorelines. We have also shown that a notable amount of the surface water (as indicated by particle concentrations) mixes with the deeper waters of the Baltic Sea.
In the Gulf of Finland, the exchange and transport processes are through the limited opening to the Northern Gotland Basin. Particles are exchanged with the Åland Sea and the Northern Gotland Basin, which makes the residence time relatively long as found in the Bay of Bothnia. The high particle concentration of 70% (Table 5.4) after 10 years also indicates a low level of exchange with the Gotland Basins. The diffusive transport dominates over the advective transport i.e., χ<1 that prolongs the residence time. The main particle path is similar to the main route of the water mass cited by Leppäranta and Myrberg [24].
The Gotland Basin, which consists of three sub-basins, is the major contributor to the exchange process in the Baltic Sea. In analogy with the present work, previous research confirm the effective mixing of the bottom and the surface waters within this basin [54]. The 22 low values of residence times as well as a high advection-diffusion ratio are also indicative of the existence of a forced advective transport process i.e., χ>>1 (Tables 5.5-5.7). The significant drop in particle concentration by the end of the 10-years period is driven by the effective redistribution of the particles among the connected basins. The hydrodynamics of the Gotland basins is more complex and involves several different processes of internal and external mixing with convective and diffusive properties [55]. The main reason is that the basin is interconnected with several basins, implying a higher and more complex exchange (Table 7.1).
In the Northern Gotland Basin both the advective and convective processes are involved i.e. the high values of advection ratio (Table 5.5). The convective transport is possible as the cooler water masses are lifted up to the warmer water layers (Figure 8). The implication is that the deeper water layers mix with the shallower water layers. The mixing process is further enhanced by the Northern Gotland basin being connected to the six neighbouring water bodies. The primary exchanging basins are the Sea of Bothnia and the Gulf of Finland that account for 76% of exchange.
Comparing the particle paths in the Western and Eastern Gotland basins, two interesting features are revealed [56]. The particles travel in all four directions in the former basin and the middle layer particles reach the surface flow in the eastern most part of the Gulf of Finland. This indicates mixing of deeper waters of the Western Gotland Basin with the sub-surface waters of the Gulf of Finland.
The main particle pathways in the Eastern Gotland Basin follow a cyclonic circulation around the Gotland Island which is the main circulation pattern in the Gotland Basin. The Gdansk Sill and Stolpe Channel are important locations where salinity and temperature fronts are formed by the incoming warmer and more saline waters from the North Sea [57]. The main transport mode in the Eastern Gotland Basin is advective as indicated by the high advection -diffusion ratio i.e., χ>>1 (Tables 5.7-5.9). The uniform distribution of the particles at the end of the simulation period also supports this suggestion.
The Bornholm and Arkona basins are the mixing basins receiving the warmer North Sea waters. The transport processes are both advective and diffusive driven by the interacting flows of the northern basins of the Baltic Sea and the North Sea [58]. Particles from Arkona Basin flow northwards along the Stolpe Channel, which is in agreement with Meier et al. [6]. Our model based maximum transport velocity is 10 cm/s, which is about 30% higher than the estimate reported in Leppäranta and Myrberg [24]. However, our higher value concerns the major inflow event in 2003.
Table 8 lists the percentage of the released particles which migrate from the deeper layers upwards into the mixing and thermocline layers after 10 years for 10 major basins of the Baltic Sea. It suggests higher degree of mixing of the deeper waters with surface water layers in the southern basins of the Baltic Sea in comparison with the northern basins [59].
There are relatively few examples available in the literature on Baltic Sea tracer transport that are comparable to our results. Meier [6] and Soomere et al. [11] were the only sources where the tracer tests are done for the river Neva and the river Kalix, and particle tracking in the Gulf of Finland, respectively. Our particle pathways for the Neva and Kalix rivers are in agreement with their results [60]. The particle paths in the Gulf of Finland are also in agreement with Soomere et al. [11] results. However, their analysis is valid only for the surface currents, which explain the limited deviations from our results (Figure 2) in Soomere et al. [11]. In addition to the Gulf of Finland, the same reference presents particle pathways entering the Baltic Sea through Öresund, Great Belt, and from the Gulf of Finland (Figure 1) in Soomere et al. [11]. There is consistency between their and our results on the particle pathways for the river Neva. In their case, the particles travel as far as the Arkona Basin which agrees with the present results in term of the travelled distance (Table 6.2 and Figure S3.d) [61]. There is also a good agreement if we compare their results for the river Neva with our results for the river Narva. This is an interesting point, as it is can imply a more active transport along the southern shorelines of the Gulf of Finland as opposed to the central region of the same [62].
The River Narva with its much lower discharge (400 m3/s) appears to play a prominent role in the transport processes. It is suggested that the jet induces a strong drag force on the ambient slow moving waters that enhances the transport close to the southern shorelines in the Gulf of Finland [63].
The particle pathways from the rivers are summarized in terms of three important features of arrival times at each shoreline, the advection properties, and the particle concentration (Tables 6.1-6.7). The results suggest that the spreading of the particles and travel times are not correlated with the river discharge [64]. An example is the river Venta which despite the lowest discharge it covers all the major basins as the river Vistula (Figures 3g and 3k). The explanation is the internal mixing of the river flow with the upper and pycnocline layers by reaching as deep as 50 m in some cases [65]. The river mixing is an important general characteristic of the river inflows that is a new result. It can be concluded that the rivers partly renew the deeper water regions and thereby maintain the low values of salinities within the basins.
There is a significant difference between rivers entering the Bay of Bothnia (Table 6.1) and the other rivers. In the former case, the particles remain mainly within the Bay of Bothnia. The rivers Neva and Daugava are interesting cases from the ecological point of view. Particle concentrations remain very high (>60%) within the released points (the Gulfs of Finland and Riga) even after 10 years.
A general-purpose, surface water hydrodynamic model GEMSS has been implemented for the Baltic Sea in order to quantify: i) internal relative exchange between major basins of the Baltic Sea, and ii) internal relative distribution of external tracer inputs via major rivers. The applicability of the hydrodynamic model has been validated against observed data for a 10 year period (2000-2009). This study provides detailed insight into drifting and spreading of inert tracers in the Baltic Sea during a recent decade that can be used as a basis for diverse environmental assessments. It extends previous studies on particle tracking in the Baltic Sea regarding both the numbers and the locations of the released particles [8-11]. Furthermore, this work provides for the first time indicators of the regional mass exchange processes between major basins covering the entire Baltic Sea as well as from major rivers; since basins and rivers are associated with surrounding countries, the results can be useful for quick estimates of the internal relative mass deliveries. The evolution of the complicated particle paths released from deep and surface waters suggest inter-basin mixing that has not been quantified for the entire basin system in previous studies [REF].
The interpolation of the particle paths in terms exchange processes between the basins of the Baltic Sea is another relevant contribution of this study. The specific conclusions of this study are summarised as follows:
• The Bay of Bothnia receives a significantly larger fraction of particles released in other basins [66], than it delivers to other basins particles released in itself; 90% of the particles released in the Bay of Bothnia remain in that basin. By contrast, 70% of particles released in the Bornholm Basin are delivered to other basins and only a small fraction of particles released in other basins is received by the Bornholm Basin. This is quantified by the limiting values of omega (eq. (1) in Table 7.1, Bay of Bothnia 0.11 and the Bornholm basin 0.72, with the remaining five of the selected major basins found to lie in between (Table 7.1).
• The Gotland basins are the major contributors to the exchange process in the Baltic Sea. The particle travel times to reach the shorelines vary significantly in the range of 50-3455 days. The dominant flow feature is advective transport in the basins.
There is evidence in support of significant mixing of the deeper waters of the Western Gotland Basin with the sub-surface waters of the Gulf of Finland.
• The transport processes in the Bornholm and Arkona basins are both advective and diffusive, driven by the interacting flows of the northern basins of the Baltic Sea and the North Sea [63]. The river inflows are characterized by the internal mixing with the upper and pycnocline layers; no evidence of the correlation between the river discharge and extent of particle spreading has been found.
• In terms of particle concentrations the three rivers Daugava, Neva and Narva have a relatively low spreading implying increased vulnerability of the Gulfs of Finland and Riga to possible pollutant and contaminated material release from these rivers. From an overall water quality perspective, the worst scenario for potential contamination of the Baltic Sea from rivers is the combination of short travel time and maximum travelled path; Vistula and Oder rivers fall within this scenario.
The authors gratefully acknowledge financial support for this research from the Central Baltic Interreg IV Programme as part of the project “Phosphorous from the seabed and water quality in archipelagos—modeling attempt (SEABED)” and the FORMAS project 2014-43 “ The Baltic Sea Region System (BALSYS)”.