Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2013) Volume 2, Issue 3
A new pressure based implicit procedure to solve the Euler and Navier-Stokes equations is developed to predict transonic viscous and inviscid flowsaround the pitching airfoil with high resolution scheme. In this process, nonorthogonal and non moving mesh with collocated finite volume formulation areused. In order to simulate pitching airfoil, oscillation of flow boundary condition is applied. The boundedness criteria for this procedure are determined from Normalized Variable Diagram (NVD) scheme. The procedure incorporates the k - ε eddy-viscosity turbulence model. In the new algorithm, the computation time is considerably reduced. This process is tested for inviscid and turbulent transonic aerodynamic flows around pitching airfoil.The results are compared with other existing numerical solutions and with experiment data. The comparisons show that the resolution quality of the developed algorithm is considerable.
<Keywords: Pitching; Transonic; Inviscid; Viscous; Boundary condition
A,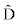 ,D : Finite difference coefficients
,D : Finite difference coefficients
C1,C2,Cμ : empirical coefficients
c : chord length
C1 : airfoil lift coefficient
ƒ : physical frequency
K : a factor in SBIC scheme to determine a special scheme
M∞ : free stream Mach number
u,v : Mean (time-average) velocity components in x and y directions
V : Velocity vector
Γ : Diffusivity coefficient
κ : reduced frequency=ωc/(2U∞)
α : angle of attack
ε : Volumetric rate of dissipation
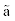 : Cell face cell
: Cell face cell
b : one-half of the chord length
Cm : airfoil moment coefficient about quarter chord
F : Flux
I : Flux
K : Kinetic energy of turbulence
T : stress tensor
U∞ : free stream velocity
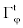 : Turbulent diffusivity coefficients
: Turbulent diffusivity coefficients
δυ : Cell volume
t : Time
αm : angle of attack in mean position
ωa : circular frequency,2pƒ
δij : Kronecker delta
G : Generation of turbulence kinetic energy
μ : Dynamic viscosity
P : Pressure
σε : Turbulent Prandtl numbers for dissipation rate
θ : angle between mean and moment chords
ρ : Density
Re : Reynolds number
μt : Turbulent viscosity
σk : Turbulent Prandtl numbers for turbulent kinetic energy
φ : Scalar quantity
In the field of Computational Fluid Dynamics (CFD), there are two categories of numerical methods for simulating moving boundary flow problems. One is the moving grid method [1], which constantly updates the grid according to the position of object. The major limitation of moving grid method is the regeneration of mesh at every time step, which may consume much time and reduce computational efficiency. To overcome this drawback, a pseudo grid-deformation approach was developed [2]. This approach calculates the grid speed through analytical expression of grid movement. The method is feasible to simulate rotational motion of the object. However, to simulate axial motion of the object, the volume change of grid cells should be considered. Another type of approaches for handling moving boundary problems is the field velocity method [3,4] which adopts the grid speed technique to simulate the velocity change of flow field. This method is especially suitable for calculation of step change of airfoil, and has been successfully applied to calculate the gust response of the airfoil/wing [5-8]. The method of conventional field velocity is usually used to calculate the indicial response by incorporating unsteady flow conditions via grid movement in CFD simulations. The main privilege of this method is direct calculation of aerodynamic responses to step changes in flow conditions. An impulsive change in the angle-of-attack can be considered as an impulsive superposition of a uniform velocity field to the free stream. The magnitude of the indicial change for the angle of attack is used for calculation of the magnitude of normal velocity. In this method, the necessity of uniform distribution of time step over the entire flow domain is guaranteed. In addition, the airfoil is not made to pitch. Hence, the influence of pure angle-of-attack and pitch rate are decoupled efficiently. A similar methodology for simulating responses of an airfoil to step changes in pitch rate and interaction with vertical gusts exists. Moreover, the field velocity method is also applied for prediction of the effects of the trailed vortex wake from the other rotor blades in helicopters, compressors or other turbo machineries. A time dependence study illustrates that a smooth and accurate solution in time requires the consistent evaluation of time metrics in order to satisfy the geometric constitutive law Sitaraman et al. [9].
The objective of the present work is to compute unsteady transonic inviscid and viscous flow fields over a pitching NACA0012 airfoil at various angles of the attack.A new pressure based implicit procedure to solve the Euler and Navier-Stokes equations is developed to predict flowsaround the pitching airfoil with high resolution scheme. In this process, nonorthogonal and non moving mesh with collocated finite volume formulation are used. In order to simulate pitching airfoil, oscillation of flow boundary condition is applied. The boundedness criteria for this procedure are determined from Normalized Variable Diagram (NVD) scheme. The procedure incorporates the k - ε eddyviscosity turbulence model. The algorithm is tested for inviscid and turbulent transonic aerodynamic flows around pitching airfoil.The results are compared with other existing numerical solutions and with experiment data. The comparisons show that the resolution quality of the developed algorithm is considerable.
Governing equations and discretization
The basic equations, which describe conservation of mass, momentum and scalar quantities, can be expressed in Cartesian tensor form as:
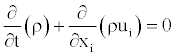 (1)
(1)
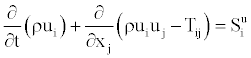 (2)
(2)
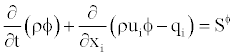 (3)
(3)
The stress tensor and scalar flux vector are usually expressed in terms of basic dependent variable. The stress tensor for a Newtonian fluid is
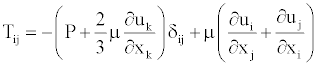 (4)
(4)
The scalar flux vector usually given by the Fourier-type law is
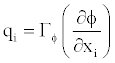 (5)
(5)
Turbulence is accounted for by adopting k -ε turbulence model. The governing
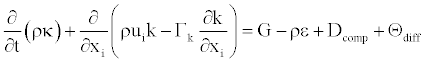 equations for (6)
equations for (6)
these quantities are
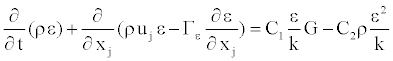 (7)
(7)
The turbulent viscosity and diffusivity coefficients are defined by
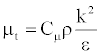 (8)
(8)
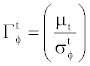 (9)
(9)
and the generation term G in equations (6) and (7) is defined by
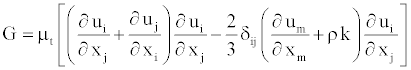 (10)
(10)
The term 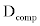 and
and 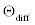 are additional k -ε contributions to the standard model often introduced to account for the effects of compressibility [10,11]. In this work, the models proposed by Yang et al. [10] are adopted, namely,
are additional k -ε contributions to the standard model often introduced to account for the effects of compressibility [10,11]. In this work, the models proposed by Yang et al. [10] are adopted, namely,
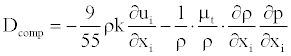 (11)
(11)
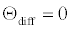 (12)
(12)
The latter being appropriate for high Reynolds number flows, as it is the case here. The values of the turbulence model coefficients used in the present work are given in (Table 1) [10].
| C1 | C2 | Cμ | σk | σε |
|---|---|---|---|---|
| 1.44 | 1.92 | 0.09 | 1.0 | 1.3 |
Table 1: Values of emperical coefficients in the standard k-ε turbulence model.
The discretization of the above differential equations is carried out using a finite-volume approach. First, the solution domain is divided into a finite number of discrete volumes or cells, where all variables are stored at their geometric centers (Figure 1). The equations are then integrated over all the control volumes by using the Gaussian theorem. The development of the discrete expressions to be presented is effected with reference to only one face of the control volume, namely, e, for the sake of brevity.
For any variable f (which may now also stand for the velocity components), the result of the integration yields
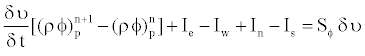 (13)
(13)
Where I(S) are the combined cell-face convection IC and diffusion ID fluxes. The diffusion flux is approximated by central differences and can be written for cell-face e of the control volume in Figure 1 as an example as:
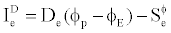 (14)
(14)
Where 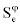 stands for cross derivative arising from mesh nonorthogonality. The discretization of the convective flux, however, requires special attention and is the subject of the various schemes developed. A representation of the convective flux for cell-face e is:
stands for cross derivative arising from mesh nonorthogonality. The discretization of the convective flux, however, requires special attention and is the subject of the various schemes developed. A representation of the convective flux for cell-face e is:
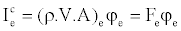 (15)
(15)
The value of the dependent variable fe is not known and should be estimated using an interpolation procedure, from the values at neighboring grid points. fe is determined by the SBIC scheme Djavareshkian [12], that it is based on the NVD technique, used for interpolation from the nodes E, P and W. The expression can be written as
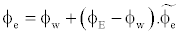 (16)
(16)
The functional relationship used in SBIC scheme for 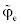 is given by
is given by
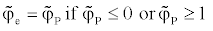
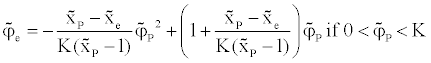 (17)
(17)
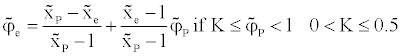
where
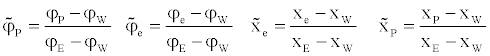 (18)
(18)
The limits on the select each value of K could be determined in the following way. Obviously the lower limit is to keep K=0, which would represent switching between upwind and central differencing. This should not be favored because; it is essential to avoid the abrupt switching between the schemes in order to achieve the converged solution. The upper limit of K is 0.5, since it represents the constant gradient and there is no need to use anything else than central differencing in that case. The value of K should be kept as low as possible in order to achieve the maximum resolution of the scheme.
According to Equation (17), if 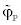 (or
(or 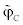 normalized variable at the central node) does not belong to [0,1], the space discretization is first order, otherwise the SBIC scheme has second order accuracy from point of view space discretization. The details of how the interpolation is made is dealt with [12]; it suffices to say that the discretized equations resulting from each approximations take the form:
normalized variable at the central node) does not belong to [0,1], the space discretization is first order, otherwise the SBIC scheme has second order accuracy from point of view space discretization. The details of how the interpolation is made is dealt with [12]; it suffices to say that the discretized equations resulting from each approximations take the form:
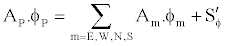 (19)
(19)
Where A(s) are the convection-diffusion coefficients. The term 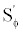 in Equation (19) contains quantities arising from non-orthogonality, numerical dissipation terms, external sources, deferred correction terms, and
in Equation (19) contains quantities arising from non-orthogonality, numerical dissipation terms, external sources, deferred correction terms, and 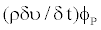 of the old time-step/iteration level. For the momentum equations it is easy to separate out the pressure-gradient source from the convected momentum fluxes.
of the old time-step/iteration level. For the momentum equations it is easy to separate out the pressure-gradient source from the convected momentum fluxes.
Solution algorithm
The set of Equation (19) is solved for the primitive variable (velocity components and energy) together with continuity utilizing pressurebased implicit sequential solution methods. The technique used is the PISO scheme presented herein Issa [13]. In this technique, the methodology has to be adapted to handle the way in which the fluxes are computed in equations (15-18). The adapted PISO scheme consists of a predictor and two corrector sequence of steps at every iteration. The predictor step solves the implicit momentum equation using the old pressure field. Thus, for example, for the component, the momentum predictor stage can be written as
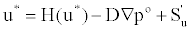 (20)
(20)
Where H contains all terms relating to the surrounding nodes and superscripts * and o denote intermediate and previous iteration values, respectively. Note that the pressure-gradient term is now written out explicitly; it is extruded from the total momentum flux by simple subtraction and addition. The corrector-step equation can be written as
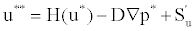 (21)
(21)
Hence, from equations (20) and (21)
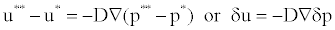 (22)
(22)
Now the continuity equation demands that
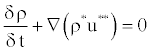 (23)
(23)
For compressible flows it is essential to account for the effect of change of density on the mass flux as the pressure changes. This is accounted for by linearizing the mass fluxes as flows
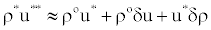 (24)
(24)
Or
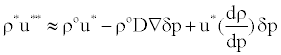
Where Equation (22) is invoked to eliminate δu and δρ is related to δp by the appropriate equation of state. Substitution of Equation (24) into Equation (23) yields a pressure-correction equation of the form
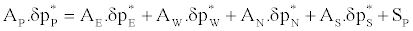 (25)
(25)
Where Sp is the finite difference analog of 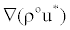 , which vanishes when the solution is converged. The A coefficients in Equation (25) take the form (the expression for AE is given as an example)
, which vanishes when the solution is converged. The A coefficients in Equation (25) take the form (the expression for AE is given as an example)
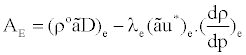 (26)
(26)
where λ is a factor whose significance is explained subsequently. The mass flux at a cell face is computed from nodal values of density and velocity, the cell-face values of ρeo and ue* in Equation (26) are not readily available. To compute those values, assumptions concerning the variations of ρ need to be made. In upwinding λ =1 when u is positive; otherwise it would be zero. Alternatively, in central difference formula λ =1/ 2 .
Such assumptions have no influence whatsoever on the final solution because they affect only the pressure-correction coefficients, and as δp goes to zero at convergence, the solution is, therefore, independent of how those coefficients are formulated; however, they do influence the convergence behavior.
The structure of the coefficients in Equation (25) simulates the hyperbolic nature of the equation system. Indeed, a closer inspection of expression (26) would reveal an upstream bias of the coefficients (A decreases as u increases), and this bias is proportional to the square of the Mach number. Also, note that the coefficients reduce identically to their incompressible form in the limit of zero Mach number.
In the present work, Crank-Nicolson scheme is applied for discretization of time derivative with second order accuracy. This option seems to be the most obvious as it requires the minimum amount of memory storage of the velocity fields. The system of equation is solved by biconjugate gradient method.
New time advancement algorithm
In this research three time advancement algorithms are used for the simulation. Figure 2 shows the flowchart of them. Algorithm 2(a) has external loop to satisfy convergence criteria for each iteration. An internal loop just for pressure equation is used in Figure 2b. The new time advancement algorithm, Figure 2c, is utilized an internal and external loop for calculation.
| κ | M∞ | αm (deg.) | αp (deg.) | c |
|---|---|---|---|---|
| 0.0814 | 0.755 | 0.016 | 2.51 | 1.0 |
Table 2: Pure pitch motion parameters.
Boundary conditions
At the inlet of the domain, only three of the four variables need to be prescribed: the total temperature, the angle of attack, and the total pressure. The pressure is obtained by zeroth order extrapolation from interior points. At outlet, the pressure is fixed. Slip boundary conditions are used on the lower and upper walls. In the case of viscous flow, the non-slip condition is applied at the airfoil surfaces. To account for the steep variations in turbulent boundary layers near solid walls, wall functions, which define the velocity profile in the vicinity of no-slip boundaries, are employed. The far-field boundary is set to 30c from the airfoil to minimize its undesired effects on the flow surrounding and is set to slip boundary conditions.
In this section, the results of the inviscid and viscous flows over a pitching NACA0012 airfoil along its quarter chord axis are indicated. The simulations are performed at a higher Reynolds number. In particular, we aim to validate the simulation with existing experiment results of a pitching airfoil, and study the lift and drag characteristics of a pitching airfoil. The steady state solutions are used as initial conditions for time-marching calculations. Figure 3 provides an illustration of pure-pitch motion for an airfoil with a mean angle of attack of αm. The parameters of motion and flow field are described in Table 2. The airfoil is forced into an oscillation around an axis located at the quarter-chord. The angle of attack is specified as:
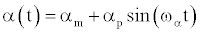 (27)
(27)
The free stream velocities for unsteady computations are set to uinlet=U∞cos(α(t)) and vinlet=U∞sin(α(t)). A H-type mesh is generated to model the airfoil and the surrounding flow. The schematic of this grid which used in the present simulation is shown in Figure 4. The grid dependence test for Navier-Stokes Equation on the NACA0012 airfoil at M∞=0.755, α=-1.8° is indicated in Figure 5. Three different mesh sizes were considered: 27680, 57950 and 115960 cells and each simulation emerged from its fully converged solution. Thus the mesh of 57980 cells was selected as a baseline mesh for further analyses. Convergence histories for the inviscid flow are shown in Figures 6 and 7 compare the computed viscous case surface pressure distribution with the experimental data [14]on NACA0012 with M∞=0.755, αm=0.016°, αp=2.51°, k=0.0814 for two angles of attacks. As it is seen from these results, there is quite a good agreement between the present method and the measurement of Landon [14]. These comparisons show that the solutions using oscillating boundary condition method has good prediction.
The computed variation of the lift coefficient versus angle of attack for inviscid and viscous flows during the third cycle is compared with that Landon [14] and Uzun [15] and in Figure 8. The existence of this variation loop is the result of induced velocities, which result in different lift coefficients between the up and down strokes. For presented viscous case, the turbulence quantities were specified at inlet to correspond to 0.008 turbulence intensity and a dissipation length scale of 10% of the airfoil chord. The value of K in SBIC scheme for this case is 0.3. Figure 8a shows the computed variation of lift coefficient versus angle of attack for viscous case which is in close agreement with experimental data. Because the flow around a pitching oscillation airfoil is disturbed and turbulence models can influence the results, the little difference between the numerical prediction and experimental data could be due to turbulence model. Figure 8b shows the Cl versus α for inviscid case. Uzun [15] used a parallel algorithm for the solution of unsteady Euler equation on unstructured reformatting grids while this study non moving mesh with oscillation of flow boundary condition is applied. It can be seen that both methods are not good agreement with experimental data particularly at the lowest angle of attack. The reason for this difference is caused by the lack of consideration of viscosity. In other words, the viscosity can effect on the separated vortex from the airfoil and aerodynamic coefficients in unsteady flow.
The predicted drag coefficients versus angle of attack are illustrated in Figure 9. The upstroke Cd and Cdmin are higher than the down stroke one. In this work, the effect of the airfoil amplitude of oscillation on the simulated lift coefficients is assessed. The instantaneous CL versus τ where K=0.0184, M=0.755 on NACA0012 is indicated in Figure 10. As illustrated, the maximum lift coefficients increases at higher amplitudes of oscillation, the calculated lift coefficients are periodic and resemble harmonic-like patterns. Furthermore, increasing amplitude endues significant lead in the CL results that CLmax is obtained at a lower τ . This can be attributed to the stronger effects of the shed wake and vertical structures on the surrounding fluid at the higher amplitudes. Table 3 indicate CPU Time comparison for different algorithms. The numbers of iterationto satisfy convergence criteria for the external loops of algorithms (a),(b) and (c) are approximately 10,000 and 1-2 respectively. For internal loops, the numbers of iterations of these algorithms are about 0, 20-30 and 2-3 respectively. As a result, the two algorithms (a) and (b) are time consuming and CPU time for new method is considerably decreased.
| Iterative Algorithm | Non-Iterative Algorithm | New Algorithm | |
|---|---|---|---|
| Internal Loop No. | - | 20-30 | 2-3 |
| External Loop No. | 1000 | 1-2 | |
| CPU Time (min) | 8600 | 2800 | 120 |
Table 3: CPU Time comparison for different algorithms.
A pressure based implicit procedure to solve the Euler and Navier- Stokes equations is developed to predict transonic viscous and inviscid flows around the pitching airfoil with high resolution scheme. In order to simulate pitching airfoil, oscillation of flow boundary condition is applied. The boundedness criteria for this procedure are determined from Normalized Variable Diagram (NVD) scheme. The main findings can be summarized as follows: 1-The pitching airfoil simulation with the oscillation of flow boundary condition with fix grid is very simple and has low cost. 2-The grid dependence test with high resolution scheme indicates that an acceptable solution can be obtained even on fairly coarse 3-The agreement between numerical and experimental data is considerable. 4-The CPU time for new method considerably reduce.