Journal of Cancer Research and Immuno-Oncology
Open Access
ISSN: 2684-1266
+44-77-2385-9429
ISSN: 2684-1266
+44-77-2385-9429
Review Article - (2023)Volume 9, Issue 2
In recent decades, there has been significant progress in conceptual, empirical and therapeutic understanding of tumor cells and innate immunity. Research has led to several practical cancer treatment approaches, including oncolytic viruses, immunotherapy and radiotherapy. Cancer polytherapy models circumvent biological and pharmacological barriers to enhance patient survival rates. Mathematical analysis of genetic variability and clinical outcomes can lead to better medication delivery regimens and biological discoveries. Cancer research must overcome the challenges associated with transferring this type of research into health centers to achieve the goals of this strategy.
Cancer; Tumor growth; Mathematical models; Treatment regimens
Cancer is the world's second leading cause of mortality worldwide, with low- and middle-income nations accounting for 70% of cancer deaths. Malignant cells undergo numerous distinguishing modifications as the tumor process progresses. Cancer treatment has traditionally depended mainly on surgery, which is frequently accompanied by chemotherapy or radiation. The utilization of virological and antigenic substances and nanotechnology supply networks has expanded our treatment options for this complicated disease [1].
There has been significant progress in cancer research and oncology, but susceptibility and tumor variability continue to be obstacles to implementing these new insights in clinical practice. This impediment is essentially a numerical genetic challenge the requirement for numerical description of various tumor cell communities and their changes constantly and during therapy. It is thus feasible to determine which medications, dosages, and regimens are optimal for a specific patient using such mathematical representations [2]. For example, if pharmaceuticals are delivered at relatively low dosages, no drug vacations are required to minimize negative consequences and patient toxicity; nevertheless, if medication is taken at greater concentrations, which may result in increased cell death, rest intervals are required to minimize adverse effects [3]. Such drug vacations might result in an exponential regrowth of the tumor cell community, posing a considerable risk of resistance development. Using these two example strategies, based on their efficacy at the time of writing, it is not clear which one will have a more significant impact on reducing tumor volume and avoiding the establishment of a robust tumor subclone. Numerous clinical investigations have been conducted to determine the optimal dose frequency. However, testing all alternative dose regimens in pre-clinical or clinical inquiries is immoral and expensive, so that only small therapeutic testing may be conducted [4].
Mathematical modeling is a good area of study because it can estimate how treatments will go and help them figure out which treatments have the fewest side effects. It is important because cancer treatment costs a lot, and new treatments are getting better and less toxic all the time. Also, mathematical models derived from empirical or therapeutic facts can be used to develop and test hypotheses, pose "what if" queries, and guide future research and validation in situ studies. These models can aid in the definition of various strategies and perhaps give insight into the mechanisms that initiate changes in complicated processes [5].
Mathematical modeling of the therapeutic efficacy of diverse cell populations is an exciting approach for restricting testing options in experimental studies and the clinical context. The mathematical modeling approach can be employed to continuously explore the thousands of alternative dose dispensation methods (each generated by a single dose-time profile). Also, polytherapy (a blend of multiple treatments given at consecutive dose-time profiles) determines which is most effective in prolonging the patient's lifespan [6]. Indeed, much scientific time has been invested in constructing computational equations that find the most efficient chemotherapy delivery protocols through optimization and control approaches. In general, these methods are targeted at substantially reducing the total tumor burden. It is essential for patients whose prognosis is long-term to rapidly diminish the tumor cell population and deal with stimulant subpopulations within the tumor. Concurrently achieving these two objectives is hampered by the fact that they are frequently done by applying conflicting developmental adaptive mechanisms. Additionally, both chronic toxicity and daily dosage negative impacts must be minimized [7].
Figure 1 depicts that the cancer is complicated because it encompasses the tumor's varied cellular components, its connection with the surroundings and immune function, and its exposure to various types of therapy. Mathematical modeling of the effect of these parameters on tumor cell population structure enables the formulation of research theories about resistance evolution and the identification of objectively appropriate therapeutic techniques that increase the likelihood of treatment (Figure 1) [8].
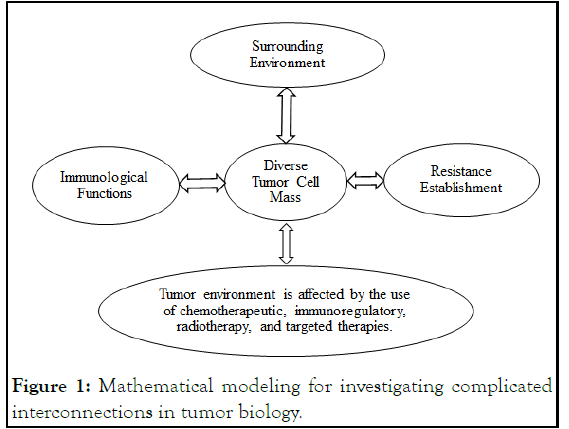
Figure 1: Mathematical modeling for investigating complicated interconnections in tumor biology.
Numerous advancements in tumor screening have been accomplished, and proteomic analysis has identified genetic variants and potential targets for developing new treatment strategies. In recent times, considerable progress has been made in standard treatment, emphasizing the most operative solutions that are likely to impact the tumor significantly [9]. This path, however, is still not easy, with generating feasible solutions encountering various obstacles. Cancer treatment now assumes that combining curative medications at their maximum tolerable dosages yields the best results. Despite this, individual medications' drug metabolism variances lead to inconsistencies in distributing effective medication doses to tumor cells. Due to the accumulated risk reported in polytherapy methods, inadequate dosages must be used to buffer the impact. In addition, determining the optimum solution procedures and navigating the consequences of standard treatment provide hurdles [10].
The purpose of this article is to conduct a comprehensive analysis of existing mathematical models used to forecast the efficacy of polytherapy mathematical models.
Cancer polytherapy mathematical models
Chemoimmunotherapy models: Disruption of tumor development and focus on detecting is typical in cancer chemotherapeutics. Yet, chemotherapy is frequently restricted due to the growth of chemo-resistance and the harm caused to healthy cells in a target organ. Recent years have seen a renewed emphasis on host-tumor connections, with evidence indicating they play a critical role in defining malignant disease symptoms and prognosis. Numerous models have been proposed to comprehend the tumor-immune relationships to identify the crucial components of an immune system's response to immunotherapy. Mathematical techniques have been used in numerous research to investigate the consequences of immunological regulation [11].
Modern cancer therapy strategies rely on particular tumors' potential to induce an innate immunity. Incorporating the immunological aspect into mathematical equations has been shown to have a critical role in medically empirical evidence such as tumor stagnation, uncontrolled tumor development, and tumor mass fluctuations. By establishing nonlinear equations that describe both the impulse response of Interleukin-2 (IL-2) and the influx of lymphocytes, it is possible to demonstrate the effects of immunology in an appropriate Ordinary Differential Equations (ODEs) model. Additionally, ODE models focused on the interaction of Natural Killer (NK) and Cluster of Differentiation (CD8+) T lymphocytes with various tumor cell types. The findings indicate that substituents cells induce a sufficient innate immunity to inhibit tumor development but influence tumor cells to escape resistance [12].
Chemotherapy for leukaemia reduces tumor volume by lowering the number of malignant cells, as shown by an ODE model study of the chemo-dynamic immunotherapy's behaviour. It has been demonstrated that a limited amount of lymphocytes must be donated in progressive therapy to achieve full relapse or cure. Additionally, the effect of chemo-resistance on treatment outcomes was studied, and a numerical equation was provided to elucidate why the pharmacologic fault occurred when a single medication was used. Finally, simulation studies indicated that chemotherapy and immunological reactions are more prospective to have a more favourable therapeutic impact [13].
Chemovirotherapy models: Many viruses had been tried in people and laboratory animals before they were first used as cancer aimed medication in the early twentieth century. Oncolytic viruses are a diverse collection of low- or nonpathogenic pathogens used to cure cancer by precisely infecting and lysing cancer cells without harming healthy cells [14].
Chemovirotherapy has been proven in recent years to boost medical properties that are difficult to achieve if each medication is administered alone. Combining antivirals with already available therapeutic approaches assists researchers in making rational investigational judgments for these medicines. To investigate the dynamics of tumor cells treated with chemovirotherapy, Partial Differential Equations (PDEs) models was devised. The suggested model included divisions with varying concentrations of healthy and afflicted tumor cells, a free pathogen, and a pharmaceutical agent. The effectiveness of oncolytic viruses was significantly dependent on the incidence and burst size of the viral disease. In addition, an ODE numerical equation and an optimum control equation were made to show how chemovirotherapy works. These models show how tumor cells, autoimmunity, and the therapeutic mixture of oncolytic viruses and chemotherapy work together. Furthermore, models suggested that the efficacy of chemovirotherapy is dependent on the magnitude of the virus burst, the pace of infection, and the dosage.
Chemoradiotherapy models: The scenario for the interaction of chemotherapy and radiotherapy requires the employment of harmful medications to combat the illness outside of the radiation source and the irradiation of isolated areas. Stochastic models for combining radiotherapy and chemotherapy were presented for combination therapy in which tumor development is modelled using source, development and terminal cells. This model included chemo and radioresistant cells and additional characteristics to quantify cells with combined tolerance. It is discovered that a schedule of dosages of chemo and radiation therapy administered alternately is more effective than screening and diagnostic tools under the same settings as it inhibits the protective subpopulation implicated for relapse [15].
Additionally, a dynamical numerical equation using integral images was built to investigate a cell line's spatial pattern and context under medication. A log cell-kill model was utilized for chemotherapeutic activities, but a linear-quadratic approach was used for irradiation impacts. This model illustrates a therapeutic potential to two established and one theoretical carcinoma medical care regimens, concluding the recommended substitute treatment was more successful. Numerous numerical methods allow for significant changes in pure radiotherapeutic and chemotherapeutic cell killing ideas.
Radioimmunotherapy models: Radioimmunotherapy for anticancer therapy has shown to be far harder to apply than first anticipated. The numerical model was developed to assess large single doses to rapid division provided in tiny amounts over a brief period. It was demonstrated that when dosage patterns are homogenous within tumors, large single doses are projected to provide a better chance of tumor remission than quickly divided therapies with the same tissue damage. When dosage patterns are diverse, the rapid division may offer a clinical value based on how different tumor absorption fractions exist.
A numerical equation for radioimmunotherapy was suggested, in which radiation dose patterns were constructed to optimize tumor survival chance, with the frequency of drug concentration considered to be sufficiently high for immediate delivery of dose distribution. The outcome revealed that the concentration and dosage pattern of tumor cells are insensitive to other designs of tumor characteristics. This analysis found that antibodies play a big part in the fight against cancer. Also, a three-dimensional numerical equation for colorimetry was developed to allocate radiation time and space diversity without requiring a diagnostic search. The results are validated by generating dosage patterns and descriptive statistics of the dosage volume from a collection of verified health information. Additionally, the study aimed to merge radio-immunotherapy with several other medical interventions, such as specific medicines and polyrhythmic treatments.
Immunovirotherapy models: A numerical equation for tumor development in response to anti-tumor oncolytic viruses and immunology was developed and examined. The scenario accounted for variability in tumor transmission pace by treating the cell cycle as a stochastic method. The linear simulation model was used to demonstrate a correlation between the anticipated cell count remaining in the cell and tumor elimination. The investigation revealed that increasing antibody mobilization effectively aids in the destruction of tumor cells throughout anti-tumor oncolytic viruses.
Radiovirotherapy models: A PDE approach was employed to describe tumor radio-virotherapy, which is an extension of previous ODE systems. As a shifting threshold issue, the simulation was performed. We established the multilateral superiority of the proposed model solutions and defined a novel specific condition related to therapeutic response. The model intended to develop possibly optimum treatment options by simulating the common effect of oncolytic viruses and radiation. Radiovirotherapy is more successful than monotherapy, as demonstrated by parametric simulations.
Targeted therapy models: Targeted treatments employ innovative anticancer agents that engage with particular biological pathways implicated in cancer growth. To establish or enhance such targeted medicines, it is necessary to understand cancer pathophysiology and characterize the interaction among tumor cells and diagnostic drugs. A fractional numerical equation for specific antibodies treatment of malignancy was suggested utilizing information from medical trials on cellular antigen uptake against humanized monoclonal antibodies. According to the analysis, the most critical criteria affecting antigen clustering are the antibody's attraction, the antibody's circulation across the tumor, and the antibody's efficiency of removal from the tumor. Nonlinear differential models have been used to simulate the randomized evolution of medicinal resistant strains. Additionally, a randomized model was presented by examining substance cells' movements and newly aggressive cells to use a set of randomized nonlinear equations. The method was verified and predicted using actual medication groupings to treat malignancy.
Additionally, conventional chemotherapy and thermochemotherapy increase endothelial function while improving the transvascular administration of anticancer drugs, ultimately lowering tumor volume. Due to the cancer drug administration during overheating, ThermoDox treatment reduces the tumor tissue. Also, polytherapy utilizing one or more anticancer medications, such as histone deacetylase inhibitors, carbonic anhydrase inhibitors, 5-hydroxytryptamine signal modulators, anti-angiogenic compounds, and therapeutic compounds affecting reactive pathways, may provide encouraging outcomes in cancer biology.
Cancer polytherapy tactics have rapidly become a standard form of therapy for oncologists and can overcome negative therapeutic impacts and medication tolerance. There is considerable concern about the safety and efficacy of merging treatment strategies. Optimally, multiple conditions would mandate the use of a specific cancer polytherapy approach, including an enhancement in the clinical situation, distinct range of safety, antibiotic resistance elimination, and experimental proof of interaction between the conversing therapeutics. Developing innovative mixtures of therapy techniques, on the other hand, is time-intensive and costly and is dependent on a profusion of characteristics specific to each malignancy. Additionally, there are various unanswered concerns regarding combined anticancer drugs. There is also a need to determine the best dose mixtures and consider the potential adverse effects of utilizing them. Such issues can be answered through numerical methods, enabling researchers to estimate pharmaceutical choices and forecast their efficacy and safety results before undertaking long and complicated studies.
Polytherapy in cancer is designed to increase the likelihood and intensity of treatment outcomes while decreasing the chances of resistance in a specific treatment. Notably, translating the principles and theoretical models into a clinical context poses practical and patient-specific obstacles to the tumor environment. It is usually challenging to transition a finding from a cell line or experimentally induced to patient medical trials. At the same time, practical considerations apply to any form of anticancer therapy; we will focus on the complications of managing tumor patients with radiation. The first difficulty associated with arranging changed or "optimized" treatment is related to the medical therapy procedure at a set time daily. Despite the logistical, physiological, and numerical difficulties that must be addressed before a theoretical values modeling technique can be successfully implemented in the field, we feel that overcoming such barriers is well valuable. The theory indicates that a numerically determined plan may be therapeutically preferable; other current and future techniques show real potential. We have high standards that logical research design will lead to fresh optimism for people with cancer.
It's worth noting that numerical methods have made a lot of progress, but there is still a significant challenge to go. Due to the complexity of cancer and its related disorders, its progression methods are incompletely defined, and hence numerical methods devised thus far are very simplistic. Therefore, it is vital to pick a new and creative polytherapy for anticancer therapy that can quickly lyse just tumor cells while enhancing the total lifespan of an individual and reducing antibiotic resistance. Mathematics is going to make a massive advance to cancer therapy. As a result, the numerical methods might be essential in selecting the ideal probabilistic method at a lower price while enhancing cancer care results in the future.
Several numerical methods given in this study overlook critical aspects of cancer evolution in the name of clarity, such as proteomics of anticancer therapy and tumor-immune connections. However, these factors impact research findings and computational findings. Accordingly, future research must apply increasingly complicated numerical models that incorporate extensive information about tumor tissues. Additionally, future numerical methods should emphasize methods apart from differential equations to include circumstances that ODEs and PDEs cannot represent. Additionally, there is an urgent need for additional research that focuses on integrating newly found mathematical concepts into medical care.
The author wants to express his deep gratitude to his research supervisor Dr. Pervaiz Iqbal for his patient guidance, enthusiastic encouragement, and helpful critiques of this research work.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Sheergojri AR, Iqbal P (2023) Treatment Strategies for Cancer Using Mathematical Models. J Cancer Res Immunooncol. 9:171.
Received: 03-Mar-2023, Manuscript No. JCRIO-23-23995; Editor assigned: 08-Mar-2023, Pre QC No. JCRIO-23-23995(PQ); Reviewed: 22-Mar-2023, QC No. JCRIO-23-23995; Revised: 12-Apr-2023, Manuscript No. JCRIO-23-23995(R); Published: 12-May-2023 , DOI: 10.35248/2684-1266.23.9.181
Copyright: © 2023 Sheergojri AR, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.