Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2010) Volume 3, Issue 4
Peptide identification by tandem mass spectrometry (MS/MS) is one of the most important problems in proteomics. Recent advances in high throughput MS/MS experiments result in huge amount of spectra, and the peptide identification process should keep pace. In this paper, we strive to achieve high accuracy and efficiency for peptide identification with the presence of noise by a two-phase filtering strategy. Our algorithm transforms spectra to high dimensional vectors, and then uses self-organizing map (SOM) and multi-point range query (MPRQ) as very efficient coarse filters to select a number of candidate peptides from database. These candidate peptides are subsequently scored and ranked by an accurate tag-based scoring function S?. Experiments showed that our approach is both fast and accurate for peptide identification.
Peptide identification by high throughput tandem mass spectrometry (MS/MS) is a very challenging problem that received wide attention by computational biologists (Eng et al., 1994; Perkins et al., 1999; Tanner et al., 2005; Taylor and Johnson, 1997; Dancik et al., 1999; Frank and Pevzner, 2005; Ma et al., 2003). The advent of high throughput mass spectrometer has made available a large amount of MS/MS spectra, and the pace of analysis of these spectra must be kept up. However, existing algorithms for peptide identification are slow and still not very accurate in the presence of noise.
Problem formulation
Here we formulate the peptide identification problem as a computational problem: Through tandem mass spectrometry, a peptide sequence ρ = (a1a2…a>l) will be fragmented into a spectrum S. The parent mass of the peptide ρ is given by 1 M=m(p)= Σ1j=l m(aj). A peptide prefix fragment is ρk = (a1a2… ak), for k ≤ l, and the prefix mass is defined as The peptide suffix fragment and suffix mass are similarly defined. A spectrum S is composed of many peaks {p1, p2,…pn}. Each of the peaks pi is represented by its intensity(pi) and mass-to-charge ratio mz(pi). If peak pi is not noise, then it will represent a fragment ion of ρ. Each peak pi can be characterized by the ion-type, that is specified by (z, t, h) € (Δz×Δt×Δh) = Δ, where z is the charge of the ion, t is the basic ion-type, and h is the neutral loss incurred by the ion. The (z, t, h)-ion of the peptide fragment q (prefix or suffix fragment) will produce an observed peak pi in the experimental spectrum S that has a mass-to-charge ratio of mz(pi). The mass of q, m(q) can be computed using a shifting function, Shift, defined as follows:
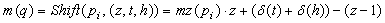 (1)
(1)
where δ(t) and δ(h) are the mass differences associated with the ion-type t and the neutral loss h, respectively. In this case, we say that peak pi is a support peak for the fragment q and we say that the fragment q is supported by the peak pi . A peak pj is a support peak for the peak pi if both of them are support peaks for the same fragment q.
In the problem of peptide identification by tandem mass spectrometry, the input is the mass spectrum S, and the output is the putative peptide sequence P from which the spectrum is generated.
The theoretical spectrum TS(P) completely characterizes the set of all possible peaks for a peptide by considering all ion-types in Δ. On the contrary, experimental spectrum seldom completely characterizes all possible peaks for peptides, and it usually contains a lot of noise.
Current approaches
Approaches for peptide identification can be categorized into database search algorithms (Eng et al., 1994; Perkins et al., 1999; Tanner et al., 2005) and De Novo algorithms (Taylor and Johnson, 1997; Dancik et al., 1999; Frank and Pevzner, 2005; Ma et al., 2003). The former return peptide sequences that best match the experimental spectrum (via some scoring functions). Apparently, the accuracies largely depend on the completeness of the database, and the process is usually slow. Additionally, they generally do not perform well for peptides not already available in the database (i.e. peptide sequences not already known).
In such situations, the De Novo algorithms are the method of choice. De Novo algorithms interpret peptide sequences from spectrum data purely by analyzing the intensity and correlation of the peaks in the spectrum data. They can retrieve tags from spectrum with high accuracy (Tanner et al., 2005), and the process is fast (always within a minute). However, their performance quickly deteriorates in the presence of noise.
Hence, how to achieve high efficiency and identification accuracy for peptide identification problem by tandem mass spectrum is already challenging in itself. As this is especially important for aiding biologists in the analysis of results in the “wet laboratory”, this paper focuses on fast and accurate peptide identification.
Recently, there is increasing research on achieving high efficiency and identification accuracy by combining database search techniques with De Novo techniques (Tanner et al., 2005; Tabb et al., 2003). For example, the GutenTAG algorithm (Tabb et al., 2003) automates the process of inferring “partial sequence tags” directly from the spectrum and efficiently examines a sequence database for peptides that match these tags. When multiple candidate peptides result from the database search, the algorithm evaluates the best match by a rapid comparison of spectral fragment ions of these candidate peptides with experimental spectrum. Similarly, the PEAKS algorithm (Ma et al., 2003) also incorporates a tag-based search module that searches the database based on highly reliable tags generated from a De Novo module.
A coarse filtering method commonly associated with database search techniques was introduced for peptide identification (Ramakrishnan et al., 2006) recently. The spectra are converted to vectors and then by using a metric distancebased indexing algorithm, initial candidate spectra (0.5% of the database) for later fine filtering are selected. A modified shared peaks count (SPC) scoring function is used to compute similarity among spectra. A Bayesian scoring scheme is then applied on candidate spectra to more accurately identify peptide sequences. However, although good efficiency can be achieved, its accuracy is not quite satisfactory. This is because spectrum comparisons approach cannot adjust well to low quality spectra. A recent algorithm, Popitam (http://www.expasy.org/tools/popitam), also incorporates a coarse filtering scheme, which is based on based on genetic programming (machine learning).
More recently, the InsPecT algorithm (Tanner et al., 2005) is proposed, which first generates a set of highly accurate tags from spectrum, and then uses these tags to filter peptide sequences in database. Another interesting aspect of InsPecT is that it uses automata constructed based on tags to search for peptide sequences. For a batch of spectrum data, the process can be very quick (about 10 ms per spectrum).
These works suggests that both coarse filtering and tagbased scoring would have positive impact on the accurate identification of peptide sequences. Previously, we have proposed the PepSOM algorithm (Ning et al., 2006) that can achieve high efficiency for peptide identification by database search based on coarse filtering (SOM and MPRQ) techniques. However, the accuracies of the PepSOM results are not very satisfactory. This is because after candidate peptides are retrieved from the database, they are scored and ranked by SPC, which is not an accurate scoring function especially on noisy spectra. Apparently, comparing candidate peptides with experimental spectrum alone is not accurate enough.
In this paper, we propose a novel peptide identification algorithm that is a combination of database search technique and De Novo technique. It has the following steps: (i) peptides in database (converted to theoretical spectrum) and experimental spectra are first converted to high-dimensional vectors; (ii) the vectors are mapped to 2D plane using self-organizing map (SOM) (Kohonen, 2001); (iii) the candidate peptides are then selected from database with multi-point range query (MPRQ) (Ng and Leong, 2004; Ng et al., 2004); and finally (iv) these candidate peptides are scored and ranked (fine filtered) by a scoring function that compares them with the experimental spectrum as well as multi-charge strong tags generated by GST-SPC (Ng et al., 2007). Steps (i)-(iii) can be regarded as coarse filtering steps, in which spectra similarity is transformed to vector similarity and then to 2D points metric distance similarity. These steps are similar to those in PepSOM. Step (iv) is a fine filtering step that scores and ranks the results. Our main objective for this twophase filtering technique is to ensure that the entire peptide identification process is fast and the final results are reliable.
Datasets for experiments
Spectrum datasets (query datasets) were obtained from Open Proteomics Database (Prince et al., 2004), PeptideAtlas database (Desiere et al., 2006) and Institute for Systems Biology (ISB) database (Keller et al., 2002). All of the experimental mass spectra were ion trap data having low mass resolution. We will refer to these datasets as OPD, PeptideAtlas and ISB datasets in the remainder of this paper. We treated Sequest result with Xcorr (cross-correlation score) ≥ 2.5 as ground truth, which is considered relatively reliable.
Spectra from OPD database (Prince et al., 2004) include the dataset of opd00001_ECOLI, Escherichia coli spectra 021112. EcoliSol 37.1(000). The spectra were obtained from E. coli HMS 174 (DE3) cell, which is grown in LB medium until ~0.6 abs (OD 600). The spectra were generated by the ThermoFinnigan ESIIon Trap “Dexa XP Plus” and the sequences for these spectra were validated by Sequest (Eng et al., 1994). There are 3,903 spectra in total – of which 1,573, 1,165 and 1,165 have parent putative charge α = 1, 2 and 3, respectively. We had chosen all the 202 spectra that were identified with Xcorr ≥ 2.5, as experimental spectra.
Spectra from PeptideAtlas database (Desiere et al., 2006) were also selected. The spectrum dataset A8_IP were obtained from Human Erythroleukemia K562 cell line. Electrospray ionization source of an LCQ Classic ion trap mass spectrometer (ThermoElectron, San Jose, CA) was used, and DTA files were generated from MS/MS spectra using TurboSequest. The dataset consists of 1,564 spectra with putative parent charge α up to 3. We had chosen all of the 44 spectra that were identified with Xcorr ≥ 2.5.
The ISB dataset (Keller et al., 2002) was generated using an ESI source from a mixture of 18 proteins, obtained from ion trap mass spectrometry, and consists of spectra of up to charge 3. The ISB dataset was of low resolution, having between 200- 700 peaks each and an average of 400 peaks. The entire dataset consists of 37,044 spectra with putative parent charge α up to 3. We had chosen all the 995 spectra that were identified with Xcorr ≥ 2.5.
The databases that we have used contain peptides from the respective protein sequences dataset. Specifically, E.coli K12 protein sequences for OPD datasets, IPI HUMAN protein sequences for PeptideAtlas dataset and human plus control protein mixture for ISB dataset were used. As the number of protein sequences were very large for PeptideAtlas (60,090) and ISB (88,374) datasets, we only used the protein sequences corresponding to spectra identified with Xcorr ≥ 2.5 (our ground truth). However, the size of databases is still very large due to many peptides. The parameters for the generation of databases, the query datasets and theoretical spectra are shown in Table 1.
| Parameters | Values | ||
|---|---|---|---|
| PeptideAtlas | OPD | ISB | |
| No. of protein sequences | 31 | 4,279 | 3,553 |
| Total database size | 9,421 | 494,049 | 1,248,212 |
| Query size | 44 | 202 | 995 |
| Fragments mass tolerance | 0.5 Da | ||
| Parent mass tolerance | 1.0 Da | ||
| Modifications | – | ||
| Charge | +2, +3 | ||
| Ion type | a, b, y, | ||
| Neutral loss | –H2O, –NH3 | ||
| Missing cleavage | 0 | ||
| Protease | Trypsin | ||
| Mass range | 0-5000 Da | ||
Table 1: Parameters for the generation of databases and theoretical spectra.
The number of experimental spectra we selected is small compared to other experiments but these experimental spectra’s corresponding peptide identification results are highly reliable. Therefore, they are suitable for reliable assessment of SOM and scoring functions. Moreover, the different ratios of experimental spectra to their three corresponding datasets will benefit the testing of SOM clustering on both small and large number of spectra data.
Two-phase filtering algorithm
Binning of Peaks: Before using SOM, binning is performed to convert peptides (transformed to theoretical spectra) in database to high-dimensional vectors in vector space. A spectrum is divided into fixed intervals by mass-to-charge ratios, whereby within each interval the peak with the highest intensity is chosen. The binning idea was used in (Pevzner et al., 2000) for mass spectrum alignment. In (Pevzner et al., 2000), the peaks of the spectrum were packed into many bins, and the spectrum was translated into sequences comprising 0’s and 1’s. We used similar method for binning, except that our binning result is a sequence of real numbers.
We have reported in previous work that given proper values of tolerances, binning can preserve the accuracies and yet decrease the computational cost greatly, especially for noisy spectra (Ning et al., 2006). For the datasets that we have used in this paper (ion trap datasets), the proper value of mass tolerance mt* is set to 0.5 Da, and the mass range of bin mbin is set to 0.25 Da. For each bin, only one single peak with the highest intensity is selected, while all the other peaks in the same bin are discarded. For each of the spectrum, the binning process thus converts it to a high-dimensional vector.
To further improve the performance of binning, we incorporated noise removal after binning. Every bin (peak) is scored. The score of a peak pi is computed by a function of the number of support peaks of pi, the intensity of pi, and mass error of pi. For the detailed function, refer to (Ng et al., 2007). Based on empirical analysis of the scores of peaks in the spectrum, the lowest 20% bins in scores ranking, and those bins with scores less than 1% of the highest one are filtered out. With the process of binning and noise removal, only those significant bins (peaks) are kept, resulting in better accuracy and efficiency.
SOM and multiple point range query: Self-organizing map (SOM) is used to transform high-dimensional vectors to 2D points on a plane (Kohonen, 2001). It is a method for unsupervised learning. In the training process, a SOM (map) is built and the neural network organizes itself using a competitive process. The SOM usually consists of a two-dimensional regular grid of nodes. The node whose weights are closest to an input vector V, termed the best-matching or winner node, is updated to be more similar to V while the winner’s neighbors are also updated (to a smaller extent) to be more similar to V. As a result, when a SOM is trained over a few thousand epochs, it gradually evolves into clusters whose data (in our case, peptides) are characterized by their similarity. Increasingly, SOM is used as an efficient and powerful tool for analyzing and extracting a wide range of biological information (Bertone and Gerstein, 2001).
The MPRQ method is used for multi-point range query on a 2D plane (Ng and Leong, 2004; Ng et al., 2004). The general idea behind MPRQ is to perform only one pass of the R-tree traversal while simultaneously processing multiple query points (in our case, query points are transformed from experimental spectra). The key observation is that when search proceeds down the R-tree, the number of query points to be processed with respect to each node also decreases rapidly. So, the query points are dynamically pruned and regenerated with respect to each node, resulting in an optimal, efficient query for each R-tree node.
SOM is useful in our algorithm because it serves two purposes: dimensionality reduction and clustering. After transforming spectrum similarity to vector similarity by binning, SOM is able to transform vector similarity to similarity in metric distance. Subsequently, MPRQ works on the 2D points to efficiently identify candidates that are similar to query spectra. Though there are other machine learning methods that serve similar purposes, we choose SOM because this method is proven to be effective on similarity search (Kohonen, 2001), and the number of candidate peptides can be easily controlled by adjusting the search distance d (introduced in MPRQ). Moreover, a SOM is very good for visualization, making it easy for biologists to identify meaningful results.
For peptide identification based on SOM and RPKM, first the theoretical spectra for the peptide sequences in the database are mapped as 2D points on a plane by SOM, and then the experimental (query) spectra are transformed into query points on the plane and proceed to query. It is possible to use many experimental spectra as query, which translates to multiple 2D points as the input for the MPRQ algorithm. Apart from a set of query points, the MPRQ algorithm also accepts as input a parameter d that controls the radius of the search distance. The larger the value of d, the more candidate peptides will be returned. MPRQ can efficiently process the multiple input points simultaneously with respect to d during query, effectively performing configurable multi-spectra similarity search on a database of known peptides. Note that similar spectra may overlap on the same 2D point, in which our algorithm builds an index of all the spectra on the same 2D point when retrieving candidates.
Tag generation method: Recently, we proposed the GST-SPC algorithm (Ng et al., 2007) which was shown to generate high quality tags (called multi-charge strong tags, or simply tags). In the first phase, GST-SPC computes a set of all tags. Then GST-SPC tries to link these tags by their mass differences, and computes a peptide sequence that is optimal with respect to shared peaks count (SPC) from all peptides derived from tags. Previous results have shown that the multi-charge strong tags generated by the first phase of GST-SPC are accurate, so in this paper we utilize these tags in scoring candidate peptides.
Scoring and ranking: To achieve high accuracy for peptide identification, the most important step is the scoring of candidate peptides selected from the database search. We have shown in previous paper (Ning et al., 2006) that by only using SPC for scoring will result in low identification accuracy. One of the main focuses in this paper is a modified scoring function; in addition to using SPC, we have also incorporated the comparison between candidate peptide and tags generated by a De Novo algorithm (the GST-SPC algorithm).
Firstly, we introduce SPC score and Stag score: (a) the SPC score is computed as the number of peaks of the same mass-charge ratio (within tolerance) between experimental spectrum and theoretical spectrum of the candidate peptide, over the number of peaks in experimental spectrum, (b) the Stag score, which measures the similarity of candidate peptide to tags, is computed as the ratio of candidate peptide that can match one or more tags at the correct position (within the range of [0,100] Da), over the length of the candidate peptide. For example, let us be given the candidate peptide “VAQLEQVYIR” and two tags “VAK” and “IVYLR” starting from the mass of 0 Da and 550 Da respectively. If we do not allow mismatch, then Stag score is computed as (3+4)/10=0.7; if we allow up to one mismatch, then Stag score is computed as (3+5)/10=0.8. To score and rank candidate peptides, we define a scoring function Sλ which is simply a weighted sum of SPC score and Stag score.
Sλ= w1.SPC + w2.Stag (2)
The weights are derived empirically based on large amounts of (experimental spectrum, peptide) pairs with high confidence in peptide identification (FDR of 0.05 or smaller, based on decoy database, details not shown here) from ISB datasets. Since the Sλ scoring function combines SPC score and Stag score, it retains the virtues of spectrum comparison by SPC, while the use of reliable tags strengthens it.
Combining the above methods is the two-phase filtering algorithm for peptide identification. Peptides from database are transformed to theoretical spectra and then transformed to vectors by binning; this is a one-off exercise for existing peptides in the database and incremental for newly identified peptides. Experimental spectra are also transformed to vectors using a similar process. Then theoretical spectra and experimental spectra are transformed to 2D points on a plane by SOM. The candidate peptides are then selected by MPRQ (Ng and Leong, 2004; Ng et al., 2004), with the transformed experimental spectra as query points. These coarse filtering steps are similar to those in PepSOM (Ning et al., 2006).
In fine filtering, the candidate peptides are then scored and ranked by comparing them with respective experimental spectrum and tags generated by GST-SPC algorithm. After the candidate peptides are generated by the SOM and MPRQ methods, the Sλ scoring function is used to score peptide-spectrum-matches.
Methods for comparison
To compare the different algorithms, the following accuracy measures were used:
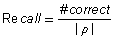 (3)
(3)
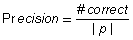 (4)
(4)
where #correct is the number of correctly identified amino acids. For any two amino acids in the correct peptide ρ and the respective identification result P, they contribute one count to #correct if and only if their positions do not have a difference of more than 100 Da (determined empirically) and they are of the same amino acid (except (I, L) as well as (K, Q), obviously). Recall indicates the quality of the sequence results with respect to the correct peptide sequence – a high recall meaning that the algorithm recovers a large portion of the correct peptide. For fair comparison with algorithms like PepNovo that only outputs the highest scoring tags (subsequences), we also use a Precision measure, which measures how many of the results are correct. Note that these recall and precision measures are different from sensitivity and specificity measures used in PepSOM (Ning et al., 2006) since there is a position constraint on amino acids in recall and precision measures, as opposed to solely using LCS to measure #correct in the sensitivity and specificity measures of PepSOM.
Experiments were performed on a PC running Linux with 3.0 GHz CPU and 1.0 GB main memory. Our algorithm is implemented in C++ and Perl. SOM_PAK (Kohonen et al., 1996) was the SOM implementation used.
Assessment of SOM and MPRQ
The next analysis is on the quality of clustering of theoretical spectra by SOM. Figure 1 gives the result of SOM clustering on OPD and ISB datasets. It is clear that theoretical spectra are well clustered on the plane. However, from the visualized maps we cannot yet tell how the 2D distance of the clustered vectors represent spectrum similarity and sequence similarity.
To assess the quality of the candidate peptides selected by SOM and MPRQ, we sampled and measured (a) the similarity of neighboring peptides (in a 2D SOM), as well as (b) the 2D distance of peptides (in a SOM) with similar sequences. The analysis of (a) will tell us whether two neighboring peptides on a SOM are indeed highly similar, as we need to be convinced that SOM is a useful tool for peptide identification. The analysis of (b) is the counterpart argument of (a), only it is meant for MPRQ.
Firstly, let us focus on (a) for now. We analyze the similarity of candidate peptides of a search range by using theoretical spectra. Results show that sequences within a search radius are more similar (by edit distance) to each other that those outside of the search radius (details not shown). The effect of search distance on the quality of the candidate peptides selected is also investigated. Previously, a search radius d = 2.5 as the MPRQ parameter was used in PepSOM (Ning et al., 2006). Here we analyze the search radius d on the accuracy of search results on three datasets of different sizes. The candidate peptides are scored and ranked by SPC score only. First-rank peptide represents the peptide with theoretical spectrum that has the highest SPC score against the experimental spectra. Best- match peptide is the peptide among all candidates that matches the “real” peptide with the highest precision and recall. Both precision and recall for first-rank and best-match peptide are computed.
Results on analysis of the search radius d (Figure 2) show that candidate peptides found within a reasonably small distance radius has very high precision and recall (0.6~0.8). It indicates that the candidate peptides within this radius are very similar to the “real” peptide. These results also show that the recall and precision of best-match peptides are much higher that those for first-rank peptides, indicating that (i) SPC score alone is not a good scoring function; and (ii) a properly designed scoring function can improve the identification accuracies significantly. The PeptideAtlas, OPD and ISB datasets are datasets of increasing order of magnitude. Results suggest that for larger datasets, the search distance used should be larger to achieve high recall and precision. Therefore, for datasets of large size, we used larger search distances. For PA dataset, among the 44 experimental spectra, 18, 24 and 31 of the corresponding “correct” peptides are within search distance d of 0.5, 1.0 and 1.5, respectively. This indicates that the identification accuracy can be very high given a good scoring function. Additionally, the precision and recall would not be significantly different with d > 1.0. Therefore, we used d = 1.0 for the PeptideAtlas dataset. Additionally, we used d = 2.5 for the OPD dataset and d = 3.5 for the ISB dataset. Figure 2(c) also shows that as search distance d increases, more candidate peptides are returned increasing both recall and precision. However, when d grows beyond the similarity clusters in the SOM, not so relevant candidates returned bring down the recall and precision values.
Secondly, let us focus on (b). To analyze the distance of similar sequences on a SOM, we picked all pairs of sequences with edit distance of 1, 2 and 3. Since the SOM is mainly composed of theoretical spectra, we have only performed analysis on theoretical spectra. It is already shown that there is no direct correlation between spectrum similarity and peptide sequence similarity (Han et al., 2004). So it is deemed sufficient to show that most of the similar sequences are in close 2D distance so that they are in search range for fine filtering later.
For sequences pairs from ISB dataset with edit distance of 1, 2, 3, the distribution of 2D distance of the sequences on SOM is illustrated in Figure 3. It is apparent that most of the similar sequences are close in each other on 2D map, and within search distance d = 3.5. Similar results are observed on OPD and PeptideAtlas datasets (details not shown here). This indicates that SOM is effective in clustering similar peptide sequences, and inline with (Ng et al., 2007) which suggests that SOM is able to cluster similar sequences.
Assessment of the quality of tags
We begin by analyzing the quality of the tags that we had generated. We measured the ratio of completely correct tags in the results, as well as the recall and precision of tags. Results are shown in Table 2. We had only analyzed the quality of tags on ISB spectra in a previous study (Ning et al., 2007). By also measuring the quality of the results on OPD and PeptideAtlas datasets, we have empirically proved the accuracy of tags (by GST-SPC algorithm) on a variety of datasets.
| Datasets | Query Size | Average Peptide length | No. of tags per Spectrum | No. of Complete Correct per Spectrum | Complete Correct Accuracy | Recall | Precision |
|---|---|---|---|---|---|---|---|
| PeptideAtlas | 44 | 10.02 | 9.76 | 6.83 | 0.70 | 0.40 | 0.36 |
| OPD | 202 | 10.14 | 7.42 | 6.01 | 0.81 | 0.43 | 0.43 |
| ISB | 995 | 19.37 | 6.19 | 4.61 | 0.74 | 0.36 | 0.32 |
Table 2: Statistical results on the quality of the generated tags. “No. of tags per spectrum” shows the average number of tags generated per spectrum. “No. of complete correct per spectrum” measures the average number of tags identified that are completely correct (i.e. identified with 100% precision). “Complete correct accuracy” is the ratio of “completely correct tags” over the total number of tags on average. The recall and precision results are obtained from tags by GST-SPC algorithm.
From Table 2, we observe that more than 1/3 of the amino acids in real peptide sequences (“recall”) can be correctly identified by tags. Also, when the tags are generated, more than 70% of them are completely correct, showing that the tags generated are reliable. Since each tag is at least one amino acid in length, it can also be observed that a significant number of tags are overlapping. For the best reliability in the following experiments, only non-overlapping tags with high scores (determined by GST-SPC algorithm) are used for peptide identification.
Peptide identification by two-phase filtering method
An important question for peptide identification is: among the candidate peptide sequences, what is the proportion of them being identical to the real peptide sequences. We term this as “complete correct accuracy”. When we consider all of the candidates, the ratio is much higher; for the PeptideAtlas dataset is 63.1%, OPD 69.5% and ISB 65.3%. And if up to two amino acids’ difference from real peptide sequence is allowed, the ratios increase to 80.1%, 85.3% and 78.6% respectively for PeptideAtlas, OPD and ISB datasets. Therefore, given a good scoring function, the peptide identification accuracy can be significantly increased. As the size of the candidate sequences generated by our algorithm is rather small (refer to Efficiency analysis section), we believe these high ratios indicate good performance of the SOM and MPRQ as coarse filtering.
Then we analyze the precision and recall for tags and peptide sequences of different lengths. It is expected that the longer the peptides, the less accurate the prediction. We discovered that (details not shown) in all of these three datasets (PeptideAtlas, OPD and ISB), tags of length 3 and 4 are of the highest precision and recall. On actual peptide sequences, it is observed that the longer the peptides, the lower the prediction accuracy. This is consistent with our prediction.
Comparison with other algorithms
Subsequently, we compared our algorithm to other peptide identification algorithms. We had selected established algorithms with freely available software or web portal: two database search algorithms, Sequest (Eng et al., 1994) and InsPecT (Tanner et al., 2005); two De Novo algorithms, Lutefisk (Taylor and Johnson, 1997) and PepNovo (Frank and Pevzner, 2005); as well as the PEAKS algorithm (Ma et al., 2003) using both De Novo and database search approach (version 4.5). For our algorithm, the Sλ scoring function is used, and the results are based on peptides with the best score. For a fair comparison, the best results (results that are ranked first by each of these algorithms) given by these algorithms were used for analysis.
We can observe from Table 3 that both precision and recall of our algorithm are better than Lutefisk and PepNovo (both De Novo algorithms). This is reasonable since De Novoalgorithms do not utilize any information from databases. Comparing their results with the quality of tags generated by our algorithm (Table 2), we noticed that the quality of tags generated by our algorithm is better than peptide identification results by Lutefisk, and comparable with that by PepNovo. Although InsPecT has higher precision, our results outperform InsPecT in recall. Specifically, for the OPD dataset, both the algorithms have precision of about 0.58, but our algorithm has higher recall. For the PeptideAtlas dataset, the precision of our algorithm is much worse than that of InsPecT, but the recall is 17% better. For the ISB dataset, both InsPecT and our algorithm have similar precision, but recall of our algorithm is higher. This means that our algorithm can identify more portion of the real peptide. Comparison with PEAKS algorithm (both De Novo and database search version) indicates that PEAKS De Novo algorithm is not as accurate as our algorithm, but PEAKS database search algorithm identifies the peptides with accuracy comparable to our algorithm.
| Datasets | Database Size | Query Size | InsPecT | Lutefisk | PepNovo | PEAKS (de novo) | PEAKS (DB search) | Our algorithm |
|---|---|---|---|---|---|---|---|---|
| PeptideAtlas | 9,421 | 44 | 0.801/0.389 | 0.149/0.057 | 0.275/0.128 | 0.239/0.247 | 0.486/0.460 | 0.521 /0.457 |
| OPD | 494,049 | 202 | 0.580/0.542 | 0.101/0.006 | 0.232/0.186 | 0.113/0.254 | 0.520/0.554 | 0.582 / 0.603 |
| ISB | 1,248,212 | 995 | 0.584/0.621 | 0.011/0.022 | 0.548/0.561 | 0.521/0.552 | 0.562/0.594 | 0.594 / 0.695 |
Table 3: Comparison of different algorithms on the accuracies of peptide identification. In each column, the “Precision/Recall” values are listed.
We have also observed that by scoring peptide candidates using Sλ, both precision and recall consistently increase (last column of Table 3), compared with only using SPC score (Figure 2). This proves the superiority of tag-based Sλ scoring function.
False Discovery Rate (FDR) (Tabb, 2008) is becoming standard for the assessment of the results of peptide identifications. Here we have analyzed the FDR of our algorithm. Due to time constraint, we performed analysis on PeptideAtlas dataset, results on other datasets should be similar. The database is generated by appending an equal number of reverse sequences as decoy to the original database. Results show that after coarse filtering, 46.4% of peptide candidates come from reverse database. After fine filtering, the distribution of scores for peptides from forward and decoy protein sequences are shown in Figure 4. It is apparent that fine filtering can separate peptides from forward and decoy database well (score = 0.1). The FDR for the final results is 5.5%, which is small. Moreover, we have observed that similar sequences are still close in 2D space (the average distance in peptide candidates from forward database is 8.07, with more than 90% within distance of 3), and the identification accuracies of our algorithm are similar compared to those without the decoy database (precision/recall of 0.505/0.444).
Efficiency analysis
One of the most important features of our algorithm is that it is very fast, especially for batch processes. For batch processing of multiple spectra query, our algorithm (without scoring of candidate peptides) can perform peptide identification for 500 spectra in less than 30 secs (e.g. for 500 spectra, 500×10.8 ms = 5.4 secs). For comparison, InsPecT needs about 10 ms on average to process one peptide (without preprocessing, details not shown here), similar to ours. For PEAKS algorithm (database search version), the average process time is less than 30 second per spectrum. Traditional database search algorithms such as Sequest are much slower than our algorithm. Though De Novo algorithms are usually faster than our algorithm, they cannot generate results with comparable accuracy.
Comparing the performance on three different datasets, we observed that increase in database size only adds to the search time of our algorithm slightly, as each query needs about 10 to 11 ms on all three datasets of vastly different sizes. Also, a large input (of many query points) does not increase the overall query time by much.
Table 4 explains the reasons that our algorithm is fast. This table is already shown in (Ning et al., 2006), but because of its importance, we have illustrated it again here. In Table 4, we see that “average candidate size” is much smaller than “database size”. Since we only need to compare each spectrum against the candidate peptides identified by MPRQ rather than the whole database, the coarse filtering rate is very low. Compared to the tandem cosine coarse filter used in (Ramakrishnan et al., 2006) which filters to around 0.5% of the database, our algorithm has a better filtering efficiency. This explains why our algorithm could achieve fast search.
| Database | Database Size | Query Size | Candidates Size | Average Candidate Size | Coarse Filtering Rate |
|---|---|---|---|---|---|
| PeptideAtlas | 9,421 | 44 | 654 | 14.9 | 0.158% |
| OPD | 494,049 | 202 | 68,610 | 339.7 | 0.069% |
| ISB | 1,248,212 | 995 | 101,443 | 102.0 | 0.008% |
Table 4: Candidates’ size, average candidate size and coarse filtering rate. “Candidates size” is the combined total results from coarse filtering of the database using the query size as input query points for the MPRQ algorithm. “Average Candidate Size” is the average peptide sequence candidates for each spectrum (query). “Coarse Filtering Rate” is computed by “average candidate size” over the database size.
Note that preprocessing the peptides in database by SOM are needed before database search. Currently, the preprocessing time for our algorithm is over an hour for all the databases, the bulk of which is time taken to generate the coordinates of the best-matching node for all the peptides in the theoretical spectrum. The actual SOM training for our largest database, ISB, takes about 15 mins while PeptideAtlas took less than 1 min to train. As for the memory needed by experiments, our algorithm have to use a large amount of space to convert the sequences database.
After database search, the scoring of candidate peptides by Sλ scoring function is approximately 5 seconds per spectrum. Such scoring is fast because both spectrum-peptide-mach and tag- peptide-match are efficient. Overall, since both coarse filtering and fine filtering are efficient, the whole two-phase filtering strategy is a very efficient strategy for peptide identification.
The program of our algorithm is available upon request.
Peptide identification by tandem mass spectrometry is a very challenging problem in proteomics. We proposed a two- phase filtering algorithm that transforms spectrum similarity to similarity of vectors, and then to metric similarity (distance) of 2D points on SOM map. After this, MPRQ could be applied as a coarse filter to produce candidate peptides efficiently. Since spectrum similarity does not have direct correlation with peptide sequences similarity, this step acts as “coarse clustering” that roughly clusters similar sequences in an effective way. Since it filtered out many unrelated spectra, which are highly unlikely to have similar sequences, the following step, fine filtering, becomes more efficient. We then applied the Sλ scoring function onto the candidate peptides, which compares each of them with experimental spectrum and highly reliable tags generated by GST-SPC algorithm. Experiments lent strong support to the fact that by using Sλ that take into consideration score based on tags, the precision and recall of our algorithm are high, yet still maintaining high efficiency, making our algorithm one of the fastest algorithms for peptide identification from mass spectrometry.
Despite the high efficiency and accuracy of this algorithm, it has some limitations. One of the limitations lies in the SOM’s imperfect clustering leading to non-neglectable false negative rate, for which other clustering method such as SVM might help to adjust the SOM clustering results. Another limitation lies in the binning process, which may be too simple to serve the purpose of effective vectorization of spectra. Sometimes, PTMs may cause mass peak shifts; information that are lost through the binning process. Vectorizing the spectra based on bins of different sizes (details not shown in this paper), that is, larger bin size at the two ends, and smaller bin sizes at the middle of the spectrum, might help in this pespective. A better, but more costly solution for this problem might be using machine learning to retrieve some representative features from spectra based on training datasets, and then vectorizing spectra based on these features.
We thank Stephan Tanner for providing us with the updated InsPecT software package and insightful discussions on it. We also thank Brian Munro of Bioinformatics Solutions Inc. for kindly providing us with the demo version of PEAKS software and helpful discussions of the results. This work was supported in part by NIH/NCI grant R01 CA-126239 and NIH/NCRR grant P41-18627.