Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
+44 1478 350008
ISSN: 2161-0398
+44 1478 350008
Research Article - (2013) Volume 3, Issue 3
The effect of grinding MgTiO3 on the particle size and electrical properties was studied. Initially, good dispersion conditions were optimized via rheological characterizations of the aqueous slurry in variant dispersant amounts. Then, 50% MgTiO3 slurry was grinded using balls of different diameter sizes (0.8 and 0.4 mm) for two consecutive cycles. The milled powder was characterized using laser granulometry, BET method, X-ray diffraction and scanning electron microscopy techniques. The crystallite size was calculated using Halder-Wagner methods. The electrical and dielectrical properties were also monitored for different particle size. These results revealed impurities from the zirconium balls, however, without affecting the particle size even if prepared with different grinding operations.
<Keywords: Grinding; Dispersion; Zeta potential; BET method; X-ray diffraction; Ceramic materials titanates
Ceramic materials for technical applications are known for more than two hundred years. Since 1970 special synthetic ceramics are designed unlike traditional materials in composition, microstructure, and properties. Additionally, special tailored ceramics are developed with large variety of chemical, electrical, biological, and mechanical properties to overcome the limitations of other conventional materials. Electronic, technological, and manufacturing industries require materials sustaining extremely high temperatures and corrosive conditions. Oxide ceramics are good candidates for such applications due to their extreme hard and corrosion resistant properties. The chemical bonding in oxide-based materials is partially covalent and partially ionic providing coating solutions at both room temperature and high temperature conditions [1].
The most important step in ceramic processing is to understand the powder properties by which can be manipulated for a better product industry. Powders are prepared by comminution process in which the solid is reduced into smaller pieces without altering its aggregate conditions. In addition, the functionality of the powder is addressed in nanotechnological applications to obtain smaller size particles at the lowest cost.
Recently, lead-free ceramics have gained attention since they cause less environmental degradation and are less harmful to human health [2]. MgTiO3 ceramics are one of the lead-free ceramics that have attracted attention lately due to its highly interesting properties and its versatile applications.
The ilmenite titanate series, M2+TiO3 (where M2+ = Ni, Mg and Mn) have high Q values, low dielectric constant and excellent optical properties. In particular, the MgTiO3 exhibit good microwave dielectrical properties of low dielectric constant (~17) and good quality factor (160000 GHz) [3]. The zero-resistance effect found between 50 and 60 K in the Mg Ti-O solid solution system is also an interesting factor [4]. It is well known that the pure or doped MgTiO3 phase presents interesting microwave dielectric properties and photoelectrical characteristics. MgTiO3 is characterized by an ilmenite structure with space group R¯3 corresponding to a hexagonal close packing of oxygen atoms. About 2/3 of the octahedral sites are occupied by cations form alternating layers characterized by the following hexagonal lattice parameters: a = 5.054 Å and c = 13.898 Å [5]. The low dielectric constant is due to the isolation of the TiO6 octahedral by the MO6 octahedron layer and the cation vacancy layer compared to the perovskite titanates. In the ilmenite structure, each TiO6 octahedron layer is sandwiched by two layers of MO6 octahedral [6].
The development of microwave dielectrics having high Q value in the high-frequency such as MgTiO3, is very important in the advancement of new media such as satellite communication and broadcasting system. MgTiO3 has a technological potential for applications in filters, antennas for communication, radar, direct broadcasting satellite and global positioning system operating at microwave frequencies [7,8]. Moreover, this material has been investigated and employed as ceramic capacitors and resonators because of its low dielectric loss and high thermal stability at high frequencies.
In the last decade nanocrystalline or nanostructured materials have proved to be very advantageous because of high fracture toughness, higher strength, lowered sintering temperature, and improved magnetic properties [9]. Companies interested in MgTiO3 products have increased the demand for fine powdered magnesium titanium oxide [9].
From a diagnostic point of view, rheological behavior is an important variable of the controlling process. Rheology affects the wet comminution of materials revealing the level of interparticle interaction or aggregation in slurry and mainly influencing the ultrafine grinding performance [10]. I our lab, we have associated either low viscosities of slurries with thin fluids for quick flow or high viscosities with thicker fluids for slow flow.
The applied rheology shear stress and shear rate are related to dynamic viscosity (μ) according to the following:
μ = Shear Stress/ Shear Rate = τ / γ = μ(Pa.sec)
A yield stress of a suspension is the stress that must be exceeded before flow will occur. The yield stress value characterizes the strength of the gel structure of a quiescent suspension.
Ceramic process suspensions are known as visco-elastic materials. This refers to the fact that they exhibit both elastic and viscous properties. Ceramic slurries are characterized by a shear thinning properties. Shear thinning fluids are fluids that are transformed under shear conditions to thin fluids. Once stress is exceeded, the yield stress and flow occur as well as the applied stress may actually fall below the yield stress value [11]. Rheological measurement characterizing the behavior of materials subjected to deformation strains is defined as the shear rate, γ. The rheological behavior of the fluid is described by one of the two flow curves τ (shear stress) = ƒ(γ) or η (viscosity) = ƒ(γ) [12].
The first step in synthesizing ceramic powder is to disperse and grind together the different powder precursors having different chemical and physical characteristics. The purpose is to make the powder react and form new phases induced by contact between the grains and processed by diffusion during the thermal cycle. Thus, the mixture of precursors must be extremely intimate and homogeneous to allow diffusion to occur as soon as possible. An intimate mixture promotes easy reaction at lower temperatures and secondary phases are avoided, as established earlier for BaTiO3 synthesis from BaCO3 and TiO2 [12]. Therefore, it is necessary that the mixture must be processed with stable and deflocculated slurries before, during, and after the grinding phase. Such approach is detrimental for every two or more raw materials are mixed such as in preparing composite ceramics.
For a suspension to be stable the well-dispersed solid particles should not gather and form clusters of either agglomerates or flocs [12]. During dispersion, agglomerates are broken to aggregate size to give rise to broad, time evolving cluster size distributions [13-16]. Fine particles below 1 μm attract each other by Van der Waals interactions to form aggregates orflocs [17,18]. Furthermore, in case of wet conditions, especially in the final stage, the fraction of particles less than 1 μm is very high. The steric forces involving polymeric dispersants are the primary mechanism involved with chemical dispersants [19].
Most ultrafine grinding processes are characterized by a high solid content and the presence of excessive fines. These are two primary factors leading to the formation of agglomerations or flocculations developing yield stress of slurry. The use of an optimal dispersant can change the surface nature of particles in the ground slurry creating inter-repulsive forces among particles [19-26]. This study aims to investigate the effects of different dispersants, quantities of dispersants, and methods of introducing dispersants on slurry rheology control under wet ultrafine grinding conditions.
Development of ceramic materials
All ceramic materials have been developed by conventional methods using solid reaction route. Since ceramic is an inorganic polycrystalline with a complex structure of grain and grain boundaries, its properties depend on its microstructure. Its properties are defined at different stages of ceramic development that transform raw materials in oxide powders into dense materials. These respective steps are given as following: selection and weighing raw materials, mixing and grinding, drying and disagglomerataion, calcinations, re-grinding, drying and disagglomerataion, pelletization (shaping) and finally sintering.
Synthesis of MgTiO3 ceramic
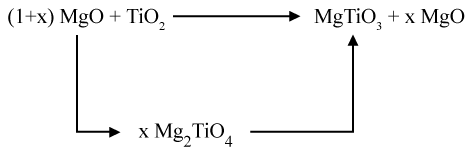
Studies published on the synthesis of MgTiO3 by Wechsler and Navrotsky reported that mixing the predecessor powders of MgTiO3;TiO2 and MgO will cause the evolution of the following three compounds: MgTiO3, Mg2TiO5, and Mg2TiO4 [27]. The last two compounds are considered as secondary phases that will influence the properties of the promising powder. These secondary phases are less stable and decompose incompletely at high temperatures to form MgTiO3 phase. In order to have a pure phase of MgTiO3 and to eliminate the two phases of Mg2TiO5 and Mg2TiO4, a certain stoechiometric ratio of the mixture MgO and TiO2 must be taken into consideration.
Sreedhar and Pavaskar has shown that adding an excess of MgO (MgO/TiO2 = 1.025) elaborates a pure phase of MgTiO3 [28]. This excess of MgO favors the formation of MgTiO3 by reacting with Mg2TiO5 formed during the evolution of the system [29,30].
To prepare 1 kg of MgTiO3, a mixture of 341.06 g of MgO powder (calcinied at 600°C for 2 hours) and 658.94 g of TiO2 anatase powder (evaporated for 12 hours at 140°C) were added into a stainless steel container. A volume of 1000 mL of water was poured to the container and mixed carefully. Then, the container was covered by a thin plastic film to prevent water loss and the mixture was kept for 12 hours to allow perfect hydration.
Methods
Mixing and grinding: The first step of the synthesis consisted of mixing and grinding oxide precursor powders for the synthesis of phase MgTiO3 by solid state reaction. The aim was to mix as intimately as possible the predecessor powders to promote the formation of the desired phase during thermal cycling (calcination) and to prevent the formation of secondary phases. For this purpose, balls (0.8 mm in diameter) of zirconium were used in a horizontal attrition mill (Dyno- Mill®, CB Mills, Gurnee, IL) to allow high-energy grinding to get rid of all the agglomerated particles of TiO2 and MgO and to ensure a well mixed and deflocculated mixture. The powder was grinded by impact or shear between the balls. The attrition was made in the presence of deionized water as a dispersing medium.
Drying and disagglomertaion: The liquid mixture obtained was exposed to 150°C to be dried. Once dried, mortar and a pestle were used to disagglomerate the solid agglomerates.
Calcination: Calcination was intended to undergo a thermal cycle to the powder mixture to obtain a crystalline nature material. Sintered powder was reacted by diffusion in the solid phase to form the desired crystalline phase. The powder was placed in the furnace at 1000°C for an hour, with increasing and decreasing ramps 150°C/h. Then formation of MgTiO3 started where diffusion of atoms took place (solid-state calcinations) according to reaction 1. The decomposition occurred at 1000°C based on reaction 2.
Re-Grinding process: Grinding was the most important step performed in this experiment to obtain ceramic particles with different properties. Our study was based on a 50% by weight MgTiO3 slurry with 50% deionized water as a dispersing medium. A quantity of 5 ml DOLAPIX dispersant was added to the slurry after being determined by rheological characterization (described later). The three component mixtures were mixed for an hour to ensure homogeneity. The slurry was then added to be grinded using the Dyno-Mill® grinding machine. The grinding cycle implemented hardly small zirconium balls with diameters smaller than one millimeter. Under such process, powders or agglomerates were sheared between small-hard zirconium balls with 55 mL total volume.
Three different grinding processes were handled by which ball size parameter was changed each time. Samples of the grinded slurry were taken at different grinding instances: 2, 5, 10, 15, 20, 25, 30, and 40 minutes. The first grinding was performed using balls of 0.8 mm diameter followed by 0.4 mm and 0.1 mm diameter balls. The characterization analysis for each sample was carried out at different grinding processes.
Characterization techniques
Different techniques were performed to characterize the obtained slurries and powders for the two grinding methods using 0.8 mm and 0.4 mm diameter balls. However, we were restricted to the granulometric analysis for the third grinding process using 0.1 mm diameter balls due to the lack of time.
Rheological characterization: To characterize the rheological behavior, a relationship between shear rate (γ) and shear stress (τ): τ = f (γ), or apparent viscosity: μ = f (γ) must be obtained using viscometer or rheometer. The rheology of the synthesized 50% by weight MgTiO3 slurry composed of 100 g water and 100 g MgTiO3 with different dispersant amounts was studied to determine the optimal dispersant (DOLAPIX) amounts that must be added during grinding. Initially, the slurry was mixed well to ensure a perfect homogenization between the dispersion medium (i.e. water) and the powder. Then, a volume of 5.5 ml DOLAPIX was added gradually at 0.5 ml interval. After each interval, the mixture was mixed for 20 minutes and then placed in the rheometer cell to be analyzed.
The principle was based on the fact that rheograms were performed with a Rheometer (Model Rheolab MC10, Physica Messtechnik, Stuttgrat, Germany). Two cells were used during the analysis; a Z4 cell for viscous slurry and a Z2 cell when the slurry turns to be fluid. The sensor used was the coaxial cylinder type (Couette geometry itself). The cylinder tank was fixed and the other cylinder was a plunger movable along a vertical axis which could vary the speed of rotation. In the annulus, the slurry was driven by the diver and held by the tank. The slurry was then subjected to a shear rate depending on the speed of rotation of the plunger. The shear stress was automatically calculated from measurements of the slip resistance torque exerted on the plunger [5]. In the obtained rheograms, the shear rate was varied between 0 – 1000 s-1, either increasing or decreasing with 50 runs in each direction. The viscosity was calculated as a result of the shear stress obtained and the shear rate exerted. The viscosity ratio between the shear stress and shear rate is expressed in pa and more traditionally in Poise (1pa.s = 10P).
Granulometric analysis: We used laser Granulometer (Model LS 230, Coulter Corp., Miami, FL) to characterize the particle size distribution for the wet samples taken at different grinding times. Drops of each liquid samples were taken and diluted with deionized water. The sample solution was injected into the measuring cell. Particles would pass through the laser radiation and the resulting data was calculated on inverted matrices. The amount of particles in water was determined using laser granulometry calculating their size distribution through laser diffraction. The diffracted beam caused a pattern of varying light intensities against angles depending upon particle diameter. Large particles caused light scattering predominantly at small angles whilst smaller particles scattered more light at larger angles. The scattered light was collected by lens and focused on a detector. The diffraction pattern was dependent on laser wavelength, particle sizes and the optical properties of the sample.
Powder characterization: Powder samples were obtained at different stages during the grinding processes exposed to different analysis and characterization techniques. These characterizations would have specific surface area, particle size, crystallographic structure, and composition.
BET specific surface area: BET method (Brunauer, Emmet and Teller) was widely used in surface science for the calculation of surface areas of solids by physical adsorption of gas molecules. Prior analysis, the powder samples were degazed by a degazing apparatus of type MicromeriticsVacPrep 061 at 300°C to ensure gas evaporation from the powder surface. The powder tubes were then set in the analysis apparatus of type Micromeritics TriStar II 3020. As well as controlled quantities of nitrogen gas were added to the samples. The sample tubes were then dipped into liquid nitrogen to ensure the adsorption. After that, samples were exposed to different pressure proportions. An electronic circuit was used to calculate the volume adsorbed and desorbed through the sample. The area S of the sample particles was estimated according to the BET method. Generally, we drew the isotherms representing the volume of gas adsorbed as a function of pressure. The BET equation (1) would linearize these curves using the concept of gas adsorbed as a monolayer:
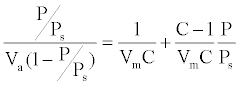 (1)
(1)
Where Va is the total volume of gas adsorbed at pressure P, Vm the volume of gas adsorbed at monolayer, Ps the saturation pressure of gas at the temperature of adsorption and C a constant related to energy adsorption. C is generally higher than 1 and P/Ps is greater than 1/C, then the equation (1) simplifies:
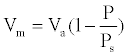 (2)
(2)
We can then determine the specific surface area S of the sample using equation (2):
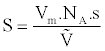 (3)
(3)
whereas the cross section of the adsorbate molecule, NA is Avogadro’s number and V is the molar volume of gas under normal conditions. The specific surface of the sample is expressed in m2/g.
XRD (X-ray Diffraction): X-ray diffraction (XRD) is an important technique for identifying, quantifying and characterizing components in complex assemblages. When a polycrystalline material or a crystalline powder is subjected to a monochromatic X-radiation, the radiation is diffracted by the lattice planes of the material. Each family of planes gives rise to a peak of diffraction angle 2θ between incident X-rays and diffracted rays, according to the inter-lattice Bragg’s formula (Equation 4):
n λ = 2dhkl sinθ (4)
A diagram showing the diffracted intensity as a function of the angle 2θ is characteristic of the crystal structure of a material. The diffraction pattern record diffractograms identify the material and its crystal structure. Therefore, purity is assessed by identifying possible secondary phases or presence of any impurities to determine lattice parameters. The intensity of the diffracted peaks depends on the multiplicity of the diffracting plane, the atoms contained in this plan by their positions, and their respective scattering factors.
The detection was held using Inel Equinox 3000 diffractometer with omega range 6° for 1800 s under X-ray dimensions of 0.2 mm thickness and 8 mm width.
Zetametric analysis: The zeta potential of the slurry particles can be used as a tool for optimizing chemical dosage to achieve the desired colloidal stability and particles distribution. Measurements were made with a Malvern Zetasizer® 3000 coupled with an automatic titrator to study the variation ζ according to the pH of the medium. Particles suspended in the liquid were subjected to an electric field E to measure the zeta potential. In this field the charged particles moved with a velocity v. We deduced the electrophoretic mobility u (expressed in m2.V-1.s-1) of the particles (Equation 5):
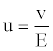 (5)
(5)
Practically, the speed of the particles was determined by the Doppler Effect, using a laser. Then, the zeta potential was ascended according to Henry’s formula (Equation 6):
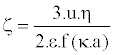 (6)
(6)
Where η and ε are respectively the viscosity and permittivity of the medium, 1/k is the thickness of the electrochemical double layer and a is the radius of the particle. The function f (κa) depends mainly on the ionic strength and the value is estimated between 1 and 1.5.
The zeta potential is expressed in mV, the measurement uncertainty is ± 3 mV.
For this measurement we chose one sample to be analyzed because the zeta potential neither depends on the particle size nor on the particle concentration. Powders were first dispersed using ultrasound in deionized water for 15 minutes. A drop of the upper part of this mixture was taken after some minutes of sedimentation and injected into the Zetasizer after being calibrated with a suspension of known potential. The pH of the dispersion was adjusted by the gradual addition of hydrochloric acid of pH=1 to measure the potential in the acidic region and ammonia of pH=12 to measure the potential in the basic region. After each adjustment, the upper surface of the mixture was withdrawn by a syringe and injected into the device to be analyzed.
Thermal dilatometric analysis: Dilatometric measurements permit the detection of the expansion and the contraction of a sample as a function of temperature and time. Dilatometry is used to determine the temperatures of early shrinkage, maximum shrinkage rate, and the possibility for the occurrence of secondary porosity. It represents the change in the sample size (shrinkage, Δx) and the rate of shrinkage versus temperature (d(Δx)/dt).
The dilatometer used Setaram TMA92® worked under controlled atmosphere. Practically, a vertical probe was kept in contact with the sample that was placed on a support (alumina) then located within a furnace. A small pressure was applied so that the probe remained in contact with the sample regardless of its shrinkage.
Structural and microstructural characterization:
Density measurements: Density of the large sintered pellets was determined after measuring their volume with a helium pycnometer (AccuPyc 1330 Micromeritics® brand) (Figure 1). The volume in the apparatus was determined by measuring the change in helium pressure between two calibrated chambers: the sample chamber and expansion chamber. Using helium, we achieved this by measuring the skeletal density of the ceramic where it presents the open porosity.
Scanning Electron Microscopy: The principle of scanning electron microscope, SEM, was based on electron-matter interactions. An electron gun bombards the material to be observed. Then, the material sent electrons by resignaling. These signals were recorded by different sensors to obtain an image or chemical analysis.
The SEM used was a Hitachi S 2460-N® tungsten filament, with a secondary electron detector, a backscattered electron detector Robinson and a micro-analysis of X-ray (EDS) Oxford Instruments brand. It was interfaced with the software Link Isis, Oxford.
Sample preparation: To perform such characterization, a characteristic sample must be prepared by pressing the powder to be observed, into 5 mm cylindrical pellets. The upper pellet’s surface was metalized by gold to ensure electron distribution on the sample’s surface.
Obtaining an image: The image of the sample surface was reconstructed through the detection of the secondary electrons and backscattered electrons emitted by the sample. They provided images for the studied surfaces. Secondary electrons were characterized by low kinetic energy ejected from the k-orbitals of the specimen atoms by inelastic scattering interactions with the electron beam. Due to their low energy, these electrons originated within a few nanometers from the sample surface. They provided a mixed picture feature of the topography of the sample. Backscattered electrons (BSE) consisted of high-energy electrons that were reflected or back-scattered out of the specimen by elastic scattering interactions with specimen atoms. BSE were used to detect contrast between areas with different chemical compositions. Because the intensity of the BSE signal was strongly related to the atomic number (Z) of the specimen, BSE images could provide information about the distribution of different elements in the sample.
Electrical and dielectrical measurements
Electrical measurements: The electrical resistivity is calculated from the measurement of insulation resistance R by the equation (7):
ρ = R × S / e (7)
where S and e represents the surface and the thickness of the sintered pellets, respectively.
Small pellets were prepared for this measurement by silver metallization of both pellet’s surfaces in order to conduct the current passing through the surfaces. These pellets were placed into a clamp-like structure in the Megohmmeter of type Sefelec M1500P with an applied voltage 1 V/μm. This set was placed in a climatic chamber SECASI SLH100/70® responsible for temperature and humidity control. The resistance was measured by Megohmmeter under 20°C temperature and 10% humidity conditions. The values of the insulation resistance were taken after 300 sec.
Dielectrical measurements: To calculate the relative permittivity, measurements of the capacitance and the dielectrical loss (tanδ) were performed using automatic programmable RLC meter (Fluke PM6306®).
Small pellets were held on the sample holder consisting two floors of 7 ports, each having two metal plates making contact by clamping the pellet to be measured. The values were taken after 5 minutes of placing the pellets.
Optimization of the slurry state
Rheology: Shear stress and viscosity variations versus different shear rates were observed to notice the rheology of 50% wt MgTiO3 water-powder slurry. Rheogram of Figure 1 confirmed the highly shear-thinning behavior of flocculated non-dispersed 50% wt MgTiO3 slurry without dispersant.
Increasing the imposed shear rate as shown in Figure 1 lowered the measured viscosity. Consequently, aggregates were destroyed and the viscosity decreased. At high shear rates after the aggregate structure had mostly been destroyed, apparent viscosities were unaffected and relatively constant. As shear rate decreased, aggregation phenomena were dominant, flocculates were rebuilt and apparent viscosities increased. This appeared by an apparent hysteresis by a difference in the accelerated and decelerated rheograms in both graphs of the shear stress and viscosity.
Attempts to stabilize the slurries and disperse the powders by steric repulsion: The above observation demonstrates the impossibility to disperse by electrostatic repulsion in aqueous slurries. To attain dispersion, steric effects were considered by adding different amounts of the dispersant DOLAPIX CA® (Table 1). The Rheology of MgTiO3 with different dispersant amounts was studied in order to determine the optimum dispersant amount that must be added to reach a dilatent shear thickening behavior.
| Total volume of dispersant in the slurry (ml) | % dispersant from the total slurry weight (%) |
|---|---|
| 0 | 0 |
| 0.5 | 0.16 |
| 1 | 0.42 |
| 1.5 | 0.75 |
| 2 | 1.10 |
| 2.5 | 1.46 |
| 3 | 1.79 |
| 3.5 | 2.05 |
| 4 | 2.38 |
| 4.5 | 2.73 |
| 5 | 3.14 |
| 5.5 | 3.34 |
Table 1: Percentages of the added dispersant amounts.
The viscosity evolution of 50% by weight of MgTiO3 slurry was achieved upon the addition of different amounts of DOLAPIX as shown in Figure 2. The rheograms revealed the shear thinning behavior of the suspension in which the viscosity decreased with increasing shear rate 0-1000 sec-1.
While adding the dispersant, we noticed that as the quantity of the dispersant was increased in the slurry, the viscosity reached lower values at lower shear rates.
It was found that the presence of different quantities of dispersant would transform the slurry through different rheological behaviors as demonstrated in Figure 3. For 50% slurry, the transition from the shear thinning behavior to the dilatant shear thickening behavior dictating the behavior of ceramic powders occurred upon addition of 5 ml of DOLAPIX dispersant i.e. 3.14% weight of the total slurry. This behavior was detected when the shear stress was eliminated after several gradual additions of dispersant amounts. For primary additions, the shear stress curves reached lower constant maximum with the increase in the dispersant amounts. An unambiguous slight dilatant behavior was obtained with 4.5 ml dispersant addition.
From the energy efficiency point of view, it was desirable for the ultrafine grinding that the addition of the optimum amount of the dispersant could increase the grinding efficiency; thus, higher achievable product fineness is attained. A 3.14% by weight DOLAPIX of the total 50% weight powder-water slurry was sufficient to obtain the optimum slurry rheology by wet ultrafine grinding. The addition of the appropriate amount of dispersant caused the elimination of the yield stress to reach the suitable rheological behavior for the ultrafine grinding.
Granulometric analysis: The grain size distribution for the first grinding process with 0.8 mm balls at different grinding durations of the slurry is given in Figure 4.
Large agglomerates reaching to 110 μm in diameter were noticed before grinding disappeared. After 5 minutes of grinding, particles of 1.5 μm in diameter representing 25% of total volume and smaller particles 0.08 μm representing 19% in volume appeared with traces of 0.02 μm particles. After 10 minutes, we achieved the largest percentage by volume of the smallest diameter particles of 0.065 μm of 30% volume. Reduction after 15 min and agglomeration of 10 μm diameter occurred. After 25 minutes grinding, we stopped the granulometric measurements because agglomerates ranging from 2-11 μm diameter started to appear.
Figure 5 shows the grain size distribution using 0.4 mm balls. Upon analyzing the resultant graphs of Figure 6, we noticed agglomerations occurred before grinding ranging from 1 to 100 μm in diameter. These agglomerations disappeared after 5 minutes grinding. A 0.06 μm particles appeared with 38% of total volume that persisted with increasing grinding times. Upon 20 and 30 minutes grinding, a range of 0.05-0.2 μm diameter particles were obtained with small agglomerate percentage at 30 min ranging between 2-4 μm diameter (not clearly obvious in Figure 5). After 40 minutes grinding, we obtained the highest percentage of the total volume 40% for the 0.075 μm diameter particles.
The evolution of the average size of particles or flocculates in suspension versus grinding time was shown in Figure 7.
We noticed the same variation behavior of the average diameter in case 0.4 mm and 0.1 mm grinding processes. The average diameter decreased for 5 min, then continued in a constant manner where the mixture became well dispersed with 0.06 μm diameter particles. However, for the 0.8 mm grinding, we observed that the average diameter decreased dramatically to low values. Flocculations of larger diameter start to form after 10 min grinding.
Powder characterization
X ray diffraction:
Composition: The X-ray powder diffraction pattern of MgTiO3 grinded with 0.8 mm and 0.4 mm balls (5, 10, 20, 30, 40 min) were shown respectively in Figure 8 and 9. Deep examination to both figures revealed the following:
For 0.8 mm grinding, the peaks ranging between 30 and 40 theta values, showed a variation in the intensity, in which their intensity increased gradually until 20 min grinding and then decreases at 30 min (Figure 8). However, 1 peak appeared in this range corresponding to aluminum, which is the main component of the XRDcell constituent.
For 0.4 mm grinding, we noticed a gradual decrease in the pattern’s peaks with increasing grinding duration with the small aluminum peak observed in the four diffractograms (Figure 9).
A closer look to the diffraction pattern showed a change in the width of the peaks pattern obtained due to variation of the crystallite size during grinding.
Halder and wagner method:
Detection of the crystallite size from the enlargement of the X-ray diffraction peaks: The half-width of the X-ray diffraction peaks allowed to determine the size of the crystallite. Indeed a diffraction ray resulted from a convolution between the instrumental ray and the true ray of the material being enlarged because of two contributions. First, the size of the crystallite was not infinite. Second, the periodicity default of the crystalline network (punctual defects, dislocations, etc…).
At first, it was necessary to perform a correction to all the instrumental diffraction rays from the resolution curves of the diffractometer recorded by monocrystals. The instrumental width of the peak half-height (indicated by β) was measured by many peaks of different angles of diffraction θ through the relation 8:
βinst=X* tan(θ) + Y/cos(θ) (8)
The experimental width was corrected through Wagner’s empirical relation (9):
β = βexp–(βinst2/βexp) (9)
Where βexp was the width value obtained by the Diffractogram and βinst was the calculated value. This relation was used by Halder and Wagner method to determine the crystallite size.
The relation that permitted to determine the average apparent size of the crystallite was:
(β* / d*)2 = (1/ε) × β* / (d*)2 + (η/2)2 (10)
Where ε was the diameter of the crystallite, η was the distortion and β* andd*given by relation 11:
β* = βcosθ / λ, d* = 2sinθ /λ (11)
with λ was the wavelength of the X-ray Plotting (β*/d*)2(nm-4) in function of β*/(d*)2(nm-3). The average diameter was obtained by the slope inverse of the line obtained. The distortion was obtained from the y-intercept [31].
Referring to Halder and Wagner, we plotted the functions of both grindings 0.8 and 0.4 mm balls (Figure 10 and 11 respectively). Values obtained when optimizing the instrumental value of β from the Quartz with the X and Y were 0.04 and 0.163, respectively.
After fitting the pattern peaks and plotting the functions required, we noticed that the crystallite diameter of 0.8 mm grinding ranges between 62 and 71.4 nm as shown in Table 2. However, the crystallite diameter decreased gradually to a minimum of 47.3 nm obtained at 30 min .4 mm grinding.
| Time of grinding (minutes) | Electrical resistivity ρ (Ω.cm) |
|---|---|
| 5 | 1.47×1015 |
| 10 | 2.41×1015 |
| 20 | 1.6×1015 |
| 40 | 1.04×1015 |
Table 2: Electrical resistivity for samples grinded using 0.8 mm diameter balls.
BET analysis: BET analysis assumed that the powder particles to be analyzed were spherically shaped. The surface area and the diameter of the particles of 0.4 and 0.8mm grinding are presented in Table 2. The two processes showed similar decreasing behavior of the particle’s diameter with increasing grinding time (Figure 12). The smallest diameter reached for both processes was at 40 min grinding.
Zeta potential and pH measurements
Zeta potential measurements were performed on a powder sample to determine the optimum pH of the slurry allowing a good dispersion of the species. We were interested in the absolute value of the zeta potentials, especially those that were higher than 20 mV. In that case, we assumed the electrostatic repulsions would be great and the slurry would be more dispersed. We noticed flocculates were form near the isoelectric point or if the zeta absolute values are lower than 20 mV. The absolute value needed for zeta potential must be at least 20 mV.
Figure 13 shows zeta potential measurements versus pH for the powder sample grinded for 40 min using 0.4 mm balls. The positive zeta potential values were less than 20 mV in the highly acidic medium confirming the existence of an unstable flocculated state. The isoelectric point, in which the repulsive forces were null, was achieved at pH = 3.5. Zeta values continued increasing in absolute term until it reached the deflocculated state at pH = 5 where |ξ| exceeded 20 mV in which the stable dispersion was attained. We noticed pH of higher than 5 seemed to be more favorable for stable and deflocculated slurries because the absolute value of the potentials measured were higher as pH increased.
The DOLAPIX used was a basic dispersant of pH=11, at which it was observed to be the best deflocculated stable state. Hence, DOLAPIX had two stabilization effects: pH and steric effect.
Thermal dilatometric analysis
Driving force for densification: The free-energy change that gave rise to densification conducted to the decrease in the surface area and lowering the surface free energy by eliminating the solid-vapor interfaces. This usually took place with the confidential formation of new and lower-energy solid-solid interface. This difference in freeenergy or chemical potential between the neck area and the surface of the particle provided a driving force which caused the transfer of the material by the fastest means available.
Controlling particle size was very important since the sintering rate was roughly proportional to the inverse of the particle size. Kingery et al. [32] was expressed by d(x2/2r)/dt denoting the rate of approach of the particles (Figure 14), and given in matter transport equation (12):
d (x2/2r)/dt = ΔV/V0= 3 (20γa3D*/ 21/2 kT) 2/5r -6/5 t 2/5 (12)
Where D* is the self diffusion coefficient, γ is the surface tension, k is Boltzmann constant, and tis the sintering time.
We have performed dilatometric analysis on the powders obtained after each grinding process to determine the ideal sintering temperature of the grinded powders. The dilatometric studies showed that the shrinkage of the all powder samples started at the same temperature around 1000°C for both grinding processes.
With respect to 0.8 mm balls grinding process (Figure 15a and 15b), increasing shrinkage rate appeared by curves shifting toward a lower temperature until the 20 min sample where the rate started to decrease by shifting toward higher temperature until it reached the slowest rate at 40 min.
Figure 15: (a) Dilatometric curves of the samples grinded with 0.8 mm diameter balls. (b) Zooming the region between 1200-1300°C. (c) Dilatometric curves of the samples grinded with 0.4 mm diameter balls. (d) Zooming the region between 1200-1300°C. (e) Variation of the % shrinkage of the 2 grinding processes versus grinding time. (f) Variation of the sintering temperature of the 2 grinding processes versus grinding time. (g) Variation of the maximum shrinkage speed of the 2 grinding processes versus grinding time.
On the other hand, the results of the shrinkage percentage of the grinding process with 0.4 mm diameter balls (Figure 15c and 15d) showed that the shrinkage curves were shifted toward a lower temperature as the grinding time progressed. Thus, the shrinkage rate process or the densification increased as the grinding time increased. This was due to the gradual decrease in the particle’s size which permitted to increase the solid-solid interface and to decrease the solidair contact with increasing the particle’s surface area.
We also noticed that the shrinkage behavior of the 0.8 mm diameter grinding was not consecutive on the contrary of the 0.4 mm diameter balls grinding process. This was due to the large agglomerates that were formed during the 0.8 mm balls grinding which appeared in the granulometric analysis after 20 minutes grinding, which was capable on increasing the solid-air interface and decreasing the sintering rate.
The shrinkage percentage of both 0.8 mm and 0.4 mm balls grinding showed a limited variation between 19 and 24% versus grinding time, Figure 15(e). However, the maximum densification was reached at lower sintering temperatures for the 0.4mm samples than that of the 0.8mm grinding process, Figure 15(f). The same behavior was noticed for the maximum shrinkage speed of both grinding processes that decreased from 0.9 to 0.6 with the evolution of grinding time, Figure 15(g).
Structure and microstructure
Density: Changes that occur during the firing process are related to (1) changes in grain size and shape, (2) changes in pore shape, and (3) changes in pore size. The changes in the porosity during the densification caused changes in the structure from a porous compact to a strong dense ceramic. In order to reach the best properties and to improve material characteristics, minimizing the porosity existing was very necessary. This happened by the transfer of the particles from one part of the structure to another.
Pycnometric measurements were performed after pressing and sintering pellets to test if low porosity was maintained. The Pycnometer gave both the skeletal volume and the density that permitted to calculate the open porosity. These specific pellets obtained could behave as good capacitors since less porosity was obtained with larger densities. Therefore, the greater the permittivity the better was the capacitance.
The pycnometer measured the real volume of the pellets without the pores. However, the total volume of the pellets including the porosity is πD2×h/4 where D and h were the diameter and the height of the cylindrical pellet after sintering, respectively. Porosity percentage was given by equation 13:
Porosity % = (ΔV/V0) ×100,ΔV=V0 -Vr (13)
With V0 was the total volume of porosity, and Vr was the pycnometric skeletal volume.
Regarding the porosity % results (Table 3), we saw that porosity reached a minimum after 20 min for the 0.8 mm diameter balls grinding, and then increased at 40 min. However, a gradual decreasing behavior was noticed for the 0.4 mm grinding process.
| Pellets | BET Diameter (μm) | Volume calculated (including porosity) V0 | Skeletal volume (pycnometric) Vr | Porosity volume (ΔV) | % porosity |
|---|---|---|---|---|---|
| 0.8 mm_5 min | 0.17 | 0.165 | 0.1376 | 0.0272 | 16.5 |
| 0.8 mm_10 min | 0.14 | 0.228 | 0.2087 | 0.019 | 8.4 |
| 0.8 mm_20 min | 0.11 | 0.226 | 0.209 | 0.017 | 7.5 |
| 0.8 mm_40 min | 0.09 | 0.223 | 0.2004 | 0.0224 | 10 |
| 0.4 mm_5 min | 0.18 | 0.223 | 0.2071 | 0.016 | 7.3 |
| 0.4 mm_10 min | 0.15 | 0.232 | 0.2181 | 0.0138 | 6 |
| 0.4 mm_20 min | 0.12 | 0.228 | 0.2149 | 0.013 | 5.7 |
| 0.4 mm_40 min | 0.10 | 0.2215 | 0.2148 | 0.007 | 3 |
Table 3: Pycnometric results.
These results were comparable with the dilatometric and granulometric analysis. Large aggregates were formed during the grinding process using 0.8 mm balls after 20 min against nonagglomerated slurry grinded with 0.4 mm balls during all grinding time. Thus, the increase in the porosity percentage at 20 min was related to the agglomerates formation and due to less sintering ability at lower rate. These results were confirmed by the dilatometric curves showed in Figure 15b and 15d.
Scanning electron microscopy: Many images were taken by the scanning electron microscopy for samples obtained by the grinding process using 0.4 mm balls. However, due to the low resolution of the SEM used, we could not specify the exact size of the particles. The SEM image of the 40 min sample grinded with 0.4 mm diameter balls showed the particles were spherically shaped verifying the BET approximation for the particle’s shape and the particle size of less than 100 nm. The structures shown in Figure 16 were aggregates of large size with aggregations of tenth of particles. These aggregates were due to the compression action of the dried grinded powder.
Electrical and dielectrical properties
Electrical properties: Table 3 resumes the electrical resistivity at 10% humidity and a temperature of 20°C for 0.8 mm grinded samples:
An ideal capacitor must have electrical resistivity larger than 1012 Ωcm. Ideal behavior was obtain with samples grinded with 0.8 mm diameter balls showing a perfect high resistivity of 1015 Ωcm.
We concluded that the grinding and the decrease in particle size did not affect the electrical properties of MgTiO3 ceramic pellets. Thus, the electrical resistivity was not related to the particle size.
Dielectrical properties: The values of the relative permittivity and dielectrical losses for the sintered samples of 0.8 mm grinding process are presented in the Table 4.
| Samples | εr | tanδ |
|---|---|---|
| 5 | 17.53 | 0.006 |
| 10 | 16.7 | 0.006 |
| 20 | 18.65 | 0.005 |
| 40 | 18.28 | 0.004 |
Table 4: Relative permittivity and dielectrical loss for samples grinded using 0.8 mm diameter balls.
tan(δ) represents the dielectrical losses a capacitor might posses. A good capacitor must have a low tan(δ) which is related to high electrical resistivity (more than 1012 Ω cm.) and a high relative permittivity (around 17 for MgTiO3).
This result was confirmed in Table 4, where losses were very low in relation with a high resistivity.
The relative permittivity was related to the structure and bonding type of the compound showing good values around 18 for all samples obtained. Thus, the dielectrical properties as observed were not affected by the particle’s size especially MgTiO3 showed good capacitance abilities with different particles size.
Since the decrease in particle size was dependent on the shear (friction) exposed by the balls on the particles (attrition) and on the shock effect of the balls on the peripheries of the grinding chamber, we may form a hypothesis from the obtained results about the mode of action of the grinder Dyno-mill. However, we could not know the predominant effect while grinding if it was either the shock or the shear because we did not know the relative strength of both actions. We proposed either the speed of the accelerator used to accelerate the movement of the balls was important in determining the efficiency of the shock factor or the increase in balls’ number as the radius of the balls decreased. We were adding a constant volume of the balls regardless of the diameter size enhancing the attrition factor to exert more shear. However, we could not form a definite conclusion concerning the occurring effect and the experiments that should be performed.
On the other hand, we tried to compare the crystallite size of the grinded powder by X-ray diffraction with the particle size obtained by different characterization techniques. The results are shown in Table 5.
| XRD | BET | Granulometer | |||
|---|---|---|---|---|---|
| Sample (0.8 mm balls) | Slope (1/ε) | Diameter (ε) μm | BET surface area (m2/g) | Diameter (μm) | Granulometer average diameter (μm) |
| 5 min | 0.016 | 0.0625 | 8.839 | 0.17 | 0.57 |
| 10 min | 0.014 | 0.0714 | 10.666 | 0.14 | 0.36 |
| 20 min | 0.014 | 0.0714 | 13.396 | 0.11 | * |
| 30 min | 0.016 | 0.0625 | 15.667 | 0.10 | * |
| 40 min | 0.015 | 0.0666 | 17.671 | 0.09 | * |
| Sample (0.4 mm balls) | Slope (1/ε) | Diameter (ε) μm | BET surface area (m2/g) | Diameter (μm) | Granulometer average diameter(μm) |
| 5 min | 0.0127 | 0.0786 | 8.3650 | 0.18 | 0.20 |
| 10 min | 0.0151 | 0.0662 | 10.234 | 0.15 | 0.10 |
| 20 min | 0.0154 | 0.0649 | 12.446 | 0.12 | 0.15 |
| 30 min | 0.0211 | 0.0473 | 16.254 | 0.09 | 0.14 |
| 40 min | 0.0194 | 0.0515 | 15.849 | 0.10 | 0.08 |
Table 5: Table of comparison of particles’ diameter by three different analysis techniques (XRD, BET& Granulometer).
There was an ambiguity with powder grains. The powder “grain size” found by laser granulometer was different from the “grain size” (or crystallite size) obtained by X-ray diffraction and BET analysis.
Noticing Table 5, the average diameter for the two grinding processes obtained by the granulometric characterization was larger than that given by BET analysis. This may be due to the dispersant present in the slurry during the grinding process. The dispersant was attached around the particles to cause dispersion. Thus, the particle’s surface area would decrease and the assumed particle’s diameter detected by laser diffraction would increase. Besides, the results of the particles diameter were calculated by a mathematical program dependent on the refractive index of the analyzed slurry. Hence, indecisiveness could exist either with the possibility for this program not to fit the case of the required slurry existing or by the inaccuracy of the refractive index. The accurate grain size could not be obtained from the granulometric analysis.
BET was performed after calcination where the dispersant was destroyed and the size measured was corresponding to MgTiO3 particles. However, the assumption of the spherically shaped particles needed to be confirmed by further analytical techniques to get the real grain size. The particle’s diameter obtained by the BET appeared to be larger than that of the XRD. The XRD characterized the crystallite in which the microscopic crystals were held together through highly defective boundaries.
We noticed that the obtained size from the grinding processes was not that of a crystallite. The size obtained was corresponding to polycrystallite that appeared to be an aggregation of 2 or 3 crystallites as a maximum. Hence, we have achieved a closer approach of obtaining particles with a size near to that of a crystallite.
The aim of the study was to decrease the particle size of the ceramic precursor powders in order to reach the smallest nanoparticle size to reach better electrical properties of the obtained nanomaterial applied in ceramic industry.
MgTiO3 was the powder chosen for this study, and the slurry worked on was a 50% by weight powder water slurry. Ultrafine grinding was the first step to be taken into consideration by optimizing the conditions in order to achieve the best results. The rheological behavior of the slurry was the most important parameter to be focused on during the grinding process. Such paramet enhanced to achieve the dilatent behavior that to obtain less viscosity. This behavior was controlled by adding 3.14% weight dispersant DOLAPIX of the total 50% weight slurry. Three grinding processes were performed using three different sized balls 0.8, 0.4, and 0.1 mm diameter balls. Samples were taken at different grinding times. Several characterization techniques were performed to detect the obtained particles: size, crystalline structure, sintering temperature, shrinkage and crystallite size for the obtained samples.
The BET results were necessary for calculating the particle diameter with a spherical shape revealed by SEM observations. However, the particle size was not greatly affected by changing the ball size. A similar decreasing behavior was detected while using 0.8 mm and 0.4 mm diameter balls. This result caused confusion about the predominance of either shear or shock actions of the balls that need to be further studied.
Agglomerates were detected for 0.8 mm grinding process showing a decrease in the shrinkage rate and an increase in the porosity percentage on the contrary of the 0.4 mm grinding process that showed consecutive results of both shrinkage and porosity.
From the XRD data, we obtained the crystallite size using Halder and Wagner method. We obtained a decreasing crystallite size with increasing grinding time for both grinding processes. When comparing these results with the BET results, we noticed that the particles obtained were polycrystallite particles. We succeeded to reach a particle size with 2 or 3 crystallites. We also noticed that the particle size was not related to the electrical and the dielectrical properties of MgTiO3 or to its ability to act with good capacitance.