Anatomy & Physiology: Current Research
Open Access
ISSN: 2161-0940
+44 1300 500008
ISSN: 2161-0940
+44 1300 500008
Review Article - (2023)Volume 13, Issue 1
Thermodynamic studies consider living entities as dissipative structures. Organisms maintain and develop an orderly structure by exchanging matter, energy, and entropy with the surrounding environment; thus, maintaining life and growth. For a single cell, the temperature, volume, content concentration, and content complexity are four control variables. For warm-blooded animals, both temperature and content concentration are assumed to be constant and only volume and content complexity, i.e., various proteins, nucleic acids, and small molecular substances in the cell and their interactions, are considered as acting variables. Thus, the potential function of a single cell should conform to the cusp catastrophe model. As the studies on the specific mathematical models of the relationship between the volume and content complexity are not available, we could not propose specific methods for the specific variants of the potential function of this cusp catastrophe model. We could only present our approximate results based on the basic characteristics of the cusp catastrophe model. We speculated that when a single cell is in a stable state, it cannot undergo differentiation, dedifferentiation, and division. These behaviors occur only when the cell enters an unstable state. Based on this speculation, we divided somatic cells of warm-blooded animals into two types, namely stable cells and non-steady cells. If we consider a warm-blooded animal as a whole dissipative structure, its control variables should have steady-state cells, non-steady-state cells, and negative entropy input. If we assume that the negative entropy input is constant, the proportion of non-steady cells and the total number of cells can be used as the control variables of the potential function. For warm-blooded animals, their potential function also conforms to the cusp catastrophe model. Because the studies on the relationship between the proportion of non-steady-state cells and the total cell number are rare, we could not propose specific methods for the variation of the potential function of this cusp catastrophe model. We could only present our approximate results according to the basic characteristics of the cusp catastrophe model. We speculated that as individuals, animals should be in a stable state during development. Once they enter an unstable state, they will fall ill or die. For humans, the proportion of non-steady cells decreases during the growth process from a fertilized egg to old age. From the fertilized egg to adulthood, the total cell number increases; however, in old age, the total cell number begins to decrease gradually. The entire developmental curve will gradually enter an unstable state. We speculated that once the developmental curve of a human enters an unstable state, it is death for the elderly.
IPS cell; System; Organisms; Mutation; Catastrophe model
When a system is distant from thermodynamic equilibrium, certain external conditions and nonlinear interactions within the system lead to a new ordered structure, a dissipative structure, which can be formed through abrupt changes. The appearance of the dissipative structure is a nonlinear effect of the system that is distant from equilibrium. Here, dissipation refers to the requirements of a system to input energy or material from the outside to maintain its new structure. The theory of dissipative structure was proposed by a Belgian scientist Prigogine while studying non-equilibrium thermodynamics. Living substances, including biological macromolecules, cells, tissues, organs, individual populations, and the entire biological world, are dissipative structures far from equilibrium. They are all nonisolated, non-equilibrated, and nonlinear systems. Organisms maintain and develop an orderly structure by exchanging matter, energy, and entropy with the surrounding environment, thus maintaining life, growth, and evolution [1].
Two different ways of change exist in the objective world; one is a smooth, continuous, and uninterrupted change, whereas another is a discontinuous leap, such as sudden rock fracture, bridge collapse, sudden slope instability, and earthquake. To study an instantaneous “catastrophe” process involved in discontinuous changes, a catastrophe theory was developed, and mathematical theories such as topology, singularity, and stability were used to study this discontinuous mutation. Under the action of small accidental disturbance factors, a stable state maintains the original state, and a non-steady state is an unsteady state that quickly leaves the original state once subjected to disturbance. The transformation of a nonlinear system from a stable state (equilibrium state) to another stable state occurs in the form of abrupt changes. The catastrophe theory is a powerful mathematical tool for studying systematic evolution and can better explain and predict catastrophic phenomena in nature and society.
The studies on the catastrophe theory in biology have mainly focused on the changes and restoration of the ecological environment, such as soil erosion and vegetation change [2]. Some studies have reported the prediction and prevention of pests [3,4]. No relevant studies on the internal self-organization of cells and the self-organization between different somatic cells of multicellular organisms are available. In this study, we used a cusp catastrophe model to preliminary and qualitatively analyze the internal self-organization of single cells and the way of selforganization of different somatic cells of multicellular organisms.
The catastrophe theory mainly investigates the leap of a certain system or process from one stable state to another stable state. The state of a system can be described by a set of parameters. When the system is in a stable state, the potential function of the cell takes an extreme value only, whereas the system is in an unstable state when parameters change within a certain range and the function has more than one extreme value.
For any cell, the model has four control variables, namely cell volume (V), cell temperature (T), cell content concentration (M), and cell component complexity (C). Therefore, we believed that the potential functions of individual cells of most organisms from bacteria to higher-order animals and plants conformed to the butterfly catastrophe model. For warm-blooded animals as an object, the analysis process was simplified, assuming that “T” and “m” were stable and not controlled variables; hence, the potential function of the cell was simplified to the cusp catastrophe model.
As a single cell contains many organelles, individually studying each organelle makes the process too complicated; hence, we classified the effect of organelles into “C” and considered it as a constant; hence, it will not be discussed again. For the calculation of “C”, we used Aristotle’s coefficient to express the number of deductive relations between various factors included in the system under study. Any factor in the study is affected by other factors. E.g., if a certain enzyme is regulated by the concentration of a target protein or hormone while being regulated by another regulatory protein and a small-molecule hormone, the deductive relationship index of this enzyme is 3. “C” is the sum of the deductive relationships of all components. As proteins are the main carriers of cell life activities, the deductive relationship of other components was excluded from this study, and the sum of the deductive relationship of proteins was used to express “C”.
The expression of the cusp catastrophe model was as follows:
V(x) = x4 + ux2 + vx
where x is the state variable (1), u and v are the control variables (2), and its phase space is three-dimensional. V(x) represents the potential, i.e., the energy stored in the system at position x. When V′(x) = 0, the system was at equilibrium, i.e., the critical point of this potential function was the solution of the equation; hence, the equilibrium surface “M” was also given by the following equation:
V′(x) = 4 × 3 + 2ux + v =0
“V” and “C” might be related to a certain degree, whereas “C” and protein levels showed a certain functional relationship. However, we have not yet found such studies on specific mathematical models, and specific data for analysis is not available. Hence, we could not propose a specific method for the reasonable variation of the potential function of this cusp catastrophe model. We only qualitatively analyzed the specific basic conditions of the cell on the basis of the theoretical characteristics of the model.
Figure 1 is the curved surface diagram of a single cell potential function with “V” and “C” as two control variables. Figure 1 shows that the potential function of a single cell is divided into a stable region and an unstable region. When each cell starts to grow, either “V” and “C” are increasing or one of them is increasing. If the growth curve is always in the stable zone, it speculates that these cells cannot undergo differentiation, dedifferentiation, division, and other cell behaviors. When the growth curve enters the unstable region, the cell has the possibility of catastrophe, i.e., certain regulatory mechanisms will specifically regulate cell behaviors such as differentiation, dedifferentiation, and division.
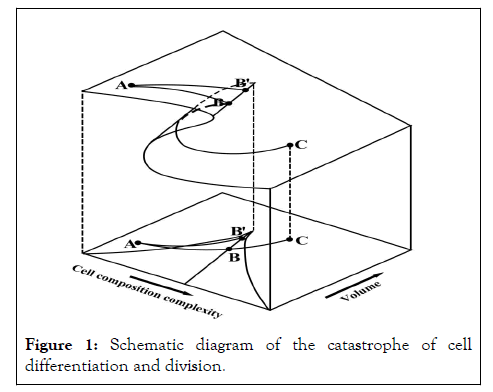
Figure 1: Schematic diagram of the catastrophe of cell differentiation and division.
When a cell is in a stable state, it can enter an unstable zone by reducing the levels of some proteins and can cause a catastrophe to the next stable state, which is differentiation (C→B→A in Figure 1). When a cell is in a stable state, it can also enter an unstable zone by increasing the levels of some proteins and can cause a catastrophe to the upper-level stable state, which is dedifferentiation (A→B→C in Figure 1). When a cell is in a stable state, it enters an unstable zone by increasing “V” and “C” and can cause a catastrophe to two stable cells, which is a division (A→B′→A in Figure 1). We only speculated that a necessary condition for the occurrence of various cell behaviors is that the cell should be in an unsteady state (Figure 1).
Studies on the role of “V” in cell differentiation are available. The activation of a zygote (referring to the structure of a diploid cell formed by the union of an egg and a sperm) genome follows a specific pattern controlled mainly by cell size [5].
The most direct evidence for the hypothesis that “C” plays an important role in cell differentiation is Induced Pluripotent Stem (IPS) cells. By introducing four regulatory factors, namely Oct3/4, Sox2, c-Myc, and Klf4, under embryonic stem cell culture conditions; adult fibroblasts could be induced into pluripotent stem cells. This is a typical dedifferentiation test. In 2010, coworkers successfully introduced mature mRNAs of Oct4, Sox2, Lin28, and Naong into human fibroblasts and obtained IPS cells. In 2011, coworkers used mature doublestranded microRNA to successfully induce mouse and human somatic cells into IPS cells. These experiments showed that increasing the levels of several regulatory proteins can facilitate reprogramming in fully differentiated cells to become undifferentiated cells, and these regulatory factors are not necessary to maintain a dedifferentiated state after dedifferentiation. This is the same as our derivation based on the catastrophe model. Increasing regulatory factors can make cells enter an unstable state before they can undergo differentiation, dedifferentiation, and division. However, to understand how increasing the levels of regulatory factors changes cell complexity, further research and data are required to establish a model [6-8].
The establishment of a specific model requires a lot of data. The research in this area is rare; hence, we could only roughly discuss the scope. First, in human beings, housekeeping genes such as tubulin gene, glycolytic enzyme gene, and ribosomal protein gene must be stably expressed in all cells as their products are necessary to maintain the basic life activities of cells. Studies have reported 575 housekeeping genes in humans [9]. In other words, the lowest stable state of the cusp catastrophe model requires the expression of 575 genes. To the highest level, we could not find a specific data analysis. Proteomics analysis showed that some human cell lines contain about 3000 to 8000 types of proteins. As studies are not available, we could only obtain a rough range similar to this. Because different cells have different functions and they occur in different environments, their shapes are irregular, and their sizes are difficult to measure. Furthermore, changes in volumes during growth are relatively subtle; hence, studies on the accurate measurement of “V” and subtle changes in “V” are needed in the future.
For warm-blooded animals such as humans, their somatic cells can be divided into two types, namely stable cells and non-steady cells. Stable cells are those cells that are fully differentiated and perform special functions. As suitable methods to detect nonsteady cells are not available, we approximated stem cells as a type of non-steady cells because stem cells of different levels can divide and differentiate. We speculated that starting from the fertilized egg, before the first fully differentiated cell is produced, all somatic cells of the entire animal are in an unstable state. When the animal grows, more fully differentiated cells can be observed, i.e., cells are in a stable state. The proportion of nonsteady- state cells is reduced. As an organism develops, the ratio of stable cells and non-steady cells changes [10]. found nestinpositive cells in both whole-brain and cerebral-cortex tissues, which were isolated and cultured from mice of different gestational ages. During the development of the mouse brain, as gestational age increased, the proportion of neural stem cells in the whole brain and cerebral cortex of the mice gradually decreased. This indirectly showed that as the body grows the ratio of non-steady cells to stable cells decreases.
We were unable to obtain specific data on the proportion of unstable cells in adult animals; however, if we consider pluripotent stem cells as a type of unstable cells, some studies are available on this proportion. Pluripotent stem cells can be isolated from the skin of mice [11,12]. and approximately 0.067% of the mouse skin cells are stem cells. If we consider stem cells as unstable cells, the proportion of unstable cells in adult mice is 0.067%.
If we consider a warm-blooded animal as a whole, its control variables are of two types, namely the proportion of non-steady cells and the total number of cells. As many types of unstable cells exist, each tissue has its unique unstable cells. If these cells are to be studied individually, the results will be too complicated; hence, we classified all unstable cells as a control variable. Two control variables were used, namely the proportion of non-steady cells and the total number of cells. Therefore, for individuals with constant temperature, their potential function also conformed to the cusp catastrophe model. A certain correlation between the proportion of non-steady-state cells and the total number of cells exists. However, as studies are not available on this correlation, we could not find suitable data to propose specific methods for the variation of the potential function of this cusp catastrophe model. We could only propose our approximate results on the basis of the basic cusp catastrophe model [13].
Because the description of the results of flat graphics is simpler and more intuitive than that of the curved surface graphics, we used flat graphics to directly analyze the potential function of the somatic cells of the warm-blooded animal. The shaded area in Figure 2 is the unstable area, and the curve is the approximate development curve of a person’s life. Because of the lack of specific data, all the graphs were trend graphs. As shown in the figure, the potential function of the warm-blooded animal as a whole is divided into a stable zone (in this range, the warmblooded animal is stable as a whole) and an unstable zone (in this range, the warm-blooded animal as a whole is unstable, may have to mutate into other forms). We speculated that as normal individuals, animals should be in a stable state during development. Once they enter an unstable state, they will fall ill or die. In the case of humans, during the growth process from a fertilized egg to old age, the proportion of non-steady cells decreases. From the fertilized egg to adulthood, the total cell mass increases, and after adulthood, the total cell mass begins to slowly decrease, and the entire development curve slowly enters an unstable state. We speculated that once the human development curve enters an unstable state, it is death for the elderly. This catastrophe model suggests that people will die unless their developmental curve is in a stable zone. This figure can also be applied to many other higher-order animals (Figure 2).
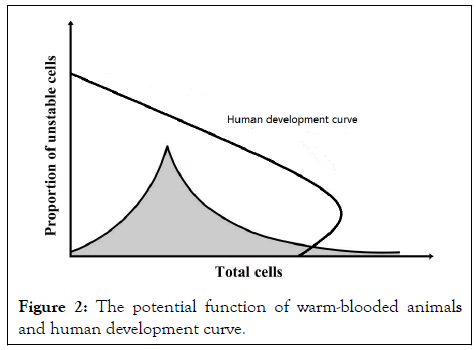
Figure 2: The potential function of warm-blooded animals and human development curve.
Combining our empirical understanding of biology with logical principles that may surpass it to create a unified theory of life is a big scientific challenge [14-17] described the origin of life from hardware (physical basis) and software (evolutionary function) through computational analogy. The adaptive system has a nested hierarchical structure, a functional optimization level, and a constraint level, and a material level. According to their research results and theories put forward, we cannot design suitable experiments to verify its correctness. Different from them, this study considered a single cell as a level to establish a catastrophe model and then used the results of the catastrophe pattern analysis at the cell level to construct a catastrophe model of multicellular organisms. From these two levels of catastrophe models, the unified operating mode of life was comprehensively considered. According to this idea, we can realize the connection between physics and molecular biology by establishing a precise mathematical model. This result has some hints for the origin of life and the artificial construction of life, that is, after establishing a complete and accurate model, if we mix thousands of proteins (or even some interactable substances) to a certain concentration based on the results, pack them into a certain small volume, make the system unstable, If the system exhibits similar split and differentiation behavior, we can verify whether the model is correct. Microbes, fungi, animals, and plants are all dissipative structures far from equilibrium and belong to the same foundation. In this study, to simplify the model and facilitate the analysis of the results, the effect of temperature was ignored. For microorganisms, lower animals, and plants, the temperature is an important control variable. Coupled with another control variable ignored in this article, that is, cell content concentration, the catastrophe model, is more complicated, which is also the physical basis of biological, morphological, and habitat diversity.
As shown in Figure 1, because the distances from the location of different types of cells to the unstable zone are not the same, their behaviors such as division, differentiation, and dedifferentiation are different. If the cells are distant from the unstable zone, the cells will not undergo differentiation or dedifferentiation. This phenomenon occurs widely in both tissue culture plants and the isolation and culture of animal cell lines. For example, callus obtained from different plants, organs, and tissues are different, and hence, their differentiation abilities are different; similarly, the isolation and culture of cell lines obtained from different tissues of different animals are different. The accurate prediction of changes required for each cell to enter the unstable zone by establishing a complete model is a promising research direction. Death is an irreversible catastrophe. This process can be described by models with the highest odd-order functions such as folding catastrophe and dovetail catastrophe. If the negative entropy of human intake is used as a control variable, the human mutation type becomes a dovetail catastrophe, which is in line with the irreversible catastrophe type; however, this analysis is more complicated than and not as intuitive as the cusp catastrophe [18-20].
Finally, the epidemiological data showed that the incidence of infectious diseases and cancer has increased sharply with age, especially; the incidence curve of many cancers follows the obvious power law. The simplest model to explain this is to assume that the occurrence of cancer is the result of the gradual accumulation of rare driver mutations in a single cell. After a cell divides many times, the DNA gradually accumulates mutations, thus transforming the normal cell into a cancer cell. The decline of the immune system with age may be an important reason for the increase in cancer incidence with age. Based on this model, as cancer cells are unstable cells because they are actively dividing, the elderly produce a certain number of cancer cells, which can keep the growth curve in a stable zone and prolong human life (Because the growth curve entering the unstable zone, the person as a whole is unstable and has to become something else). When people grow old, the body may actively produce some cancer cells to maintain system stability.
[Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Ding W, Qiang J, Wang M, Zhu H, Cao Z (2023) Use of the Catastrophe Model to Preliminarily Explore the Principles of Multicellular Organisms. Anat Physiol. 13:409.
Received: 06-Jan-2023, Manuscript No. APCR-23-21279; Editor assigned: 10-Jan-2023, Pre QC No. APCR-23-21279 (PQ); Reviewed: 24-Jan-2023, QC No. APCR-23-21279; Revised: 03-Feb-2023, Manuscript No. APCR-23-21279 (R); Published: 10-Feb-2023 , DOI: 10.35248/2161-0940.23.13.409
Copyright: © 2023 Cao Z, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.