Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 1
Measures of Exchange Market Pressure (EMP) combine exchange-rate depreciations, reserve losses, and interest-rate hikes into a single index, for the purpose of explaining or predicting currency crisis. The standard measure assigns variance-smoothing weights that are fixed throughout the sample periods. Here, we extend the static PCA analysis of Hegerty (2013) to model EMP using the Dynamic Principal Components (DPCA) approach of Forni et al. While the DPCA and the: “standard” measure match in certain cases, they diverge widely in others, suggesting that this alternative must be refined before it can be used in wider practice.
<Keywords: Exchange market pressure; Dynamic principal components; Time series
In studies of currency crises, “crisis” episodes are often calculated as periods in which a currency depreciates or a central bank intervenes to defend it. A weighted measure of both possibilities is termed an Exchange Market Pressure (EMP) Index. Extreme values are deemed to be “crisis” periods, with a binary variable equaling one during these times, although continuous EMP measures are also used in econometric studies.
One criticism of the calculation of EMP measures is the weighting scheme for each component. Most are not based on underlying theory and may be biased. Girton and Roper [1] assigned equal weights to currency depreciations and reserve losses, while Weymark [2] estimated a structural model to calculate them. In the most common EMP measure, Eichengreen, Rose and Wyplosz [3], (hereafter referred to as ERW) simply deflate each of three components—they also include interest-rate increases—by its own standard deviation so that the most volatile component will not dominate the series. Pentecost et al. [4] apply Principal Components Analysis (PCA) to assign weights, without much success. In a more detailed study, Hegerty [5,6] uses PCA to generate monthly EMP series for 21 countries. He arrives at two key conclusions. First, in no case is the first principal component valid, since the weights are often of the “wrong” sign. Secondly, when the second or third component is used in empirical analyses and compared with the ERW measure, “crisis” periods and estimation results differ. So far, no study has come up with a credible alternative to the ERW measure of EMP.
This study can be considered a brief extension of Hegerty [5,6], except that here, the Dynamic Principal Components Analysis of Forni et al. [7] is used. Calculating DPCA measures for 19 emerging markets in Latin America, Central Europe, and Asia, we find that these often differ greatly from a parallel ERW measure both in terms of the properties of the data series and the results of a basic estimation. We conclude that DPCA is not statistically superior to the much-criticized ERW measure.
Using monthly data from the International Financial Statistics of the International Monetary Fund, we generate two EMP series for each of 19 countries over the period from 2001 m01 to 2009 m08. The ERW measure is calculated as per Equation (1):
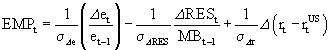 (1)
(1)
Reserve losses are scaled by the lagged monetary base, and each interest-rate differentials (money market rate) are, like nominal exchange rates, taken vis-à-vis the U.S. dollar. The second measure, using DPCA, assigns time-varying weights to the same three components.
Following Hegerty [5,6] for each of the three geographic areas, we enter all relevant countries’ EMP series in a single regional vector. This vector also includes world commodity prices and the U.S. Standard and Poor’s stock index to capture external events. We do this separately for the ERW and DPCA measures, for a total of six vectors. This allows us to conduct Granger causality tests for spillovers. Examining the timeseries plots, basic descriptive statistics, and Granger causality tests, we can assess how each series pair differs, and whether one series is more sensitive and more likely to point to a currency “crisis.”
Finally, we generate Impulse Response Functions (IRFs) for the DPCA vectors to address how each EMP series responds to shocks to the other variables. Since all IRFs’ results depend on the ordering of the variables in a VAR, a choice must be made regarding this issue. Traditionally, the variables are placed in order of endogeneity, as per the “orthogonal” VARs of Sims [8]. Here, however, we use the Generalized VAR approach of Pesaran and Shin [9], which is invariant to the ordering of the variables. Our results are explained below.
Figure 1 depicts our two EMP measures for each country. While the two measures for Hong Kong clearly are dissimilar, other countries— such as Mexico, Uruguay, Bulgaria, Ukraine, and the Philippines— have DPCA measures that appear to match the ERW measures quite closely. Little consistent pattern emerges. Malaysia’s ERW measure fluctuates more than its DPCA measure, while Brazil and Ukraine register “spikes” that are much larger for the new measure. Table 1 suggests that the DPCA series tend to have larger standard deviations than their ERW counterparts.
| Panel A: DPCA Exchange Market Pressure | Panel B: ERW Exchange Market Pressure | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Max | Min | S.D. | Mean | Median | Max | Min | S.D. | ||
| Latin America | Latin America | ||||||||||
| Brazil | -0.354 | -0.803 | 19.339 | -7.948 | 4.08 | Brazil | -0.521 | -0.492 | 5.319 | -6.008 | 1.569 |
| Chile | -0.029 | -0.228 | 14.247 | -5.14 | 2.561 | Chile | -0.301 | -0.16 | 4.831 | -6.653 | 1.556 |
| Colombia | -0.031 | -0.435 | 10.26 | -6.699 | 3.048 | Colombia | -0.408 | -0.412 | 3.693 | -4.331 | 1.492 |
| Mexico | 0.39 | 0.226 | 12.323 | -7.859 | 2.197 | Mexico | -0.213 | -0.049 | 7.857 | -6.301 | 1.671 |
| Uruguay | 0.181 | 0.022 | 17.201 | -7.488 | 3.01 | Uruguay | -0.048 | -0.337 | 11.173 | -6.155 | 2.347 |
| Central and Eastern Europe | Central and Eastern Europe | ||||||||||
| Bulgaria | -0.436 | -0.442 | 6.267 | -5.583 | 2.038 | Bulgaria | -0.501 | -0.504 | 6.278 | -5.535 | 1.672 |
| Croatia | -0.512 | -0.884 | 7.533 | -5.562 | 2.277 | Croatia | -0.358 | -0.48 | 8.007 | -6.55 | 2.089 |
| Czech Republic | -0.489 | -0.715 | 5.12 | -6.596 | 2.359 | Czech Republic | -0.383 | -0.397 | 7.752 | -9.064 | 1.704 |
| Latvia | -0.262 | -0.357 | 6.774 | -4.132 | 1.728 | Latvia | -0.314 | -0.301 | 6.533 | -13.869 | 2.043 |
| Lithuania | -0.466 | -0.408 | 4.73 | -4.682 | 1.87 | Lithuania | -0.353 | -0.393 | 4.886 | -5.828 | 1.561 |
| Poland | -0.204 | -0.628 | 12.07 | -6.339 | 3.387 | Poland | -0.459 | -0.45 | 5.788 | -4.74 | 1.58 |
| Romania | 0.036 | 0.01 | 5.729 | -6.357 | 2.337 | Romania | -0.876 | -0.945 | 7.746 | -6.265 | 1.93 |
| Ukraine | 0.355 | -0.023 | 19.669 | -3.24 | 2.767 | Ukraine | -0.325 | -0.45 | 6.762 | -4.906 | 1.778 |
| Asia | Asia | ||||||||||
| Hong Kong | -0.008 | 0.001 | 0.261 | -0.345 | 0.104 | Hong Kong | -0.484 | -0.446 | 3.253 | -5.132 | 1.82 |
| Indonesia | 0.025 | -0.087 | 12.709 | -7.615 | 2.574 | Indonesia | -0.292 | -0.463 | 4.785 | -5.146 | 1.666 |
| Japan | -0.196 | 0.003 | 6.311 | -6.257 | 2.382 | Japan | -0.228 | -0.401 | 6.113 | -3.274 | 1.402 |
| Korea | -0.016 | -0.219 | 12.075 | -7.681 | 2.502 | Korea | -0.509 | -0.567 | 6.768 | -5.261 | 1.615 |
| Malaysia | -0.119 | -0.163 | 2.156 | -1.733 | 0.739 | Malaysia | -0.375 | -0.5 | 9.16 | -3.307 | 1.906 |
| Philippines | -0.053 | -0.011 | 3.905 | -3.535 | 1.156 | Philippines | -0.538 | -0.418 | 6.886 | -6.334 | 1.973 |
Table 1: Descriptive Statistics.
Tables 2-4 show that the differences also persist when VAR models are estimated that use each EMP measure. Poland’s ERW measure, to name one example, registers a spillover from world commodity prices but not U.S. stocks, but these are exactly reversed when the DPCA measure is used. Clearly, the DPCA measure of EMP is not a reliable alternative to the traditional ERW measure until the technique is further refined.
| Brazil | DPCA | ERW | Mexico | DPCA | ERW |
| Excluded | Prob. | Prob. | Excluded | Prob. | Prob. |
| CHIL | 0.915 | 0.942 | BRA | 0.383 | 0.848 |
| COL | 0.174 | 0.265 | CHIL | 0.816 | 0.722 |
| MEX | 0.915 | 0.582 | COL | 0.276 | 0.535 |
| URU | 0.198 | 0.761 | URU | 0.809 | 0.639 |
| WCP | 0.119 | 0.591 | WCP | 0.636 | 0.92 |
| S&P | 0.011 | 0.035 | S&P | 0.058 | 0.001 |
| All | 0.006 | 0.436 | All | 0.128 | 0.016 |
| Chile | DPCA | ERW | Uruguay | DPCA | ERW |
| Excluded | Prob. | Prob. | Excluded | Prob. | Prob. |
| BRA | 0.978 | 0.677 | BRA | 0.048 | 0.536 |
| COL | 0.05 | 0.192 | CHIL | 0.214 | 0.971 |
| MEX | 0.089 | 0.63 | COL | 0.57 | 0.002 |
| URU | 0.633 | 0.773 | MEX | 0.856 | 0.787 |
| WCP | 0.875 | 0.581 | WCP | 0.605 | 0.575 |
| S&P | 0.208 | 0.72 | S&P | 0.599 | 0.032 |
| All | 0.262 | 0.858 | All | 0.356 | 0.021 |
| Colombia | DPCA | ERW | |||
| Excluded | Prob. | Prob. | |||
| BRA | 0.415 | 0.726 | |||
| CHIL | 0.821 | 0.279 | |||
| MEX | 0.828 | 0.726 | |||
| URU | 0.142 | 0.602 | |||
| WCP | 0.486 | 0.475 | |||
| S&P | 0.012 | 0.522 | |||
| All | 0.087 | 0.724 | |||
Table 2: VAR Granger Causality/Block Exogeneity Wald Tests: Latin America.
| Bulgaria Excluded | DPCA Prob. | ERW Prob. | Latvia Excluded | DPCA Prob. | ERW Prob. |
| CRO | 0.636 | 0.068 | BUL | 0.494 | 0.839 |
| CZE | 0.706 | 0.154 | CRO | 0.89 | 0.98 |
| LAT | 0.494 | 0.781 | CZE | 0.234 | 0.724 |
| LIT | 0.509 | 0.13 | LIT | 0.734 | 0.976 |
| POL | 0.557 | 0.161 | POL | 0.877 | 0.25 |
| ROM | 0.377 | 0.272 | ROM | 0.999 | 0.723 |
| UKR | 0.416 | 0.103 | UKR | 0.173 | 0.019 |
| WCP | 0.699 | 0.091 | WCP | 0.252 | 0.049 |
| S&P | 0.066 | 0.121 | S&P | 0.034 | 0.06 |
| All | 0.801 | 0.05 | All | 0.274 | 0.205 |
| Croatia Excluded | DPCA Prob. | ERW Prob. | Lithuania Excluded | DPCA Prob. | ERW Prob. |
| BUL | 0.964 | 0.863 | BUL | 0.343 | 0.742 |
| CZE | 0.63 | 0.905 | CRO | 0.837 | 0.109 |
| LAT | 0.342 | 0.83 | CZE | 0.124 | 0.609 |
| LIT | 0.183 | 0.757 | LAT | 0.952 | 0.622 |
| POL | 0.755 | 0.259 | POL | 0.486 | 0.574 |
| ROM | 0.692 | 0.169 | ROM | 0.195 | 0.281 |
| UKR | 0.805 | 0.041 | UKR | 0.929 | 0 |
| WCP | 0.702 | 0.207 | WCP | 0.691 | 0.03 |
| S&P | 0.023 | 0.143 | S&P | 0.132 | 0.079 |
| All | 0.571 | 0.455 | All | 0.476 | 0.005 |
| Czech R. Excluded |
DPCA Prob. |
ERW Prob. |
Poland Excluded |
DPCA Prob. |
ERW Prob. |
| BUL | 0.699 | 0.439 | BUL | 0.208 | 0.099 |
| CRO | 0.267 | 0.562 | CRO | 0.612 | 0.846 |
| LAT | 0.89 | 0.81 | CZE | 0.284 | 0.087 |
| LIT | 0.038 | 0.874 | LAT | 0.711 | 0.553 |
| POL | 0.706 | 0.425 | LIT | 0.342 | 0.122 |
| ROM | 0.335 | 0.317 | ROM | 0.488 | 0.596 |
| UKR | 0.872 | 0.209 | UKR | 0.84 | 0.618 |
| WCP | 0.818 | 0.989 | WCP | 0.122 | 0.006 |
| S&P | 0.061 | 0.886 | S&P | 0.016 | 0.483 |
| All | 0.311 | 0.94 | All | 0.189 | 0.023 |
| Romania Excluded | DPCA Prob. | ERW Prob. | Ukraine Excluded | DPCA Prob. | ERW Prob. |
| BUL | 0.896 | 0.922 | BUL | 0.022 | 0.601 |
| CRO | 0.201 | 0.385 | CRO | 0.599 | 0.686 |
| CZE | 0.375 | 0.992 | CZE | 0.179 | 0.607 |
| LAT | 0.197 | 0.298 | LAT | 0.008 | 0.187 |
| LIT | 0.245 | 0.095 | LIT | 0.615 | 0.751 |
| POL | 0.536 | 0.139 | POL | 0.036 | 0.156 |
| UKR | 0.904 | 0.622 | ROM | 0.92 | 0.261 |
| WCP | 0.24 | 0.44 | WCP | 0.044 | 0.486 |
| S&P | 0.541 | 0.747 | S&P | 0.008 | 0.392 |
| All | 0.58 | 0.493 | All | 0 | 0.275 |
Table 3: VAR Granger Causality/Block Exogeneity Wald Tests: Central and Eastern Europe.
| Hong Kong Excluded | DPCA Prob. | ERW Prob. | Korea Excluded | DPCA Prob. | ERW Prob. |
| INDO | 0.129 | 0.349 | HK | 0.673 | 0.863 |
| JPN | 0.977 | 0.881 | INDO | 0.577 | 0.112 |
| KOR | 0.798 | 0.329 | JPN | 0.301 | 0.816 |
| MALA | 0.029 | 0.003 | MALA | 0.644 | 0.244 |
| PHI | 0.708 | 0.807 | PHI | 0.115 | 0.142 |
| S&P | 0.57 | 0.748 | S&P | 0.08 | 0.092 |
| All | 0.163 | 0.015 | All | 0.297 | 0.163 |
| Indonesia Excluded | DPCA Prob. | ERW Prob. | Malaysia Excluded | DPCA Prob. | ERW Prob. |
| HK | 0.489 | 0.366 | HK | 0.671 | 0.802 |
| JPN | 0.227 | 0.951 | INDO | 0.196 | 0.954 |
| KOR | 0.039 | 0.995 | JPN | 0.125 | 0.302 |
| MALA | 0.888 | 0.228 | KOR | 0.009 | 0.02 |
| PHI | 0.889 | 0.625 | PHI | 0.004 | 0.628 |
| WCP | 0.347 | 0.932 | WCP | 0.549 | 0.413 |
| S&P | 0 | 0.248 | S&P | 0.028 | 0.236 |
| Japan Excluded | DPCA Prob. | ERW Prob. | Philippines Excluded | DPCA Prob. | ERW Prob. |
| HK | 0.664 | 0.549 | HK | 0.32 | 0.742 |
| INDO | 0.511 | 0.711 | INDO | 0.074 | 0.67 |
| KOR | 0.266 | 0.141 | JPN | 0.085 | 0.677 |
| MALA | 0.844 | 0.787 | KOR | 0.463 | 0.535 |
| PHI | 0.357 | 0.027 | MALA | 0.548 | 0.021 |
| WCP | 0.761 | 0.92 | WCP | 0.086 | 0.038 |
| S&P | 0.735 | 0.078 | S&P | 0.902 | 0.54 |
| All | 0.718 | 0.234 | All | 0.069 | 0.069 |
Table 4: VAR Granger Causality/Block Exogeneity Wald Tests: Asia
What results do these relatively novel DPCA measures provide, when applied to our model? We generate GIRFs for our Latin American, Central/East European, and Asian vectors in Figures 2-4. In general, the U.S. S and P index has a negative effect on EMP; in other words, stock-price declines result in increased EMP in most of these emerging markets. Changes in world commodity prices have more limited effects. The other effects, particularly bilateral linkages, vary from country to country.
For example, Brazil’s exchange market is highly sensitive; EMP is affected by shocks to nearly all Latin American economies. Uruguay’s EMP responds to Brazilian shocks as well. Chile is particularly impacted by Colombia. Colombia’s EMP responds to Uruguayan EMP, and vice versa. Mexico is only weakly affected by Chile, Colombia, and Brazil.
On the other hand, CEE countries are less affected by their neighbors. Ukraine is the main exception; its EMP responds positively to all neighbors (and negatively to world commodity prices). Interestingly, Latvia responds negatively to Ukrainian EMP; similar findings have been found in Hegerty [10]. Likewise, the Asian countries in our study show limited effects, even to world commodity prices. Only Indonesia seems to be affected by these prices, as well as the U.S. stock market. In all, these limited results, like those of our Granger Causality tests, suggest that the DPCA measure of EMP fails to uncover results that were shown in earlier studies that use standard approaches. Future research will have to refine this method.
While the weighting scheme of the EMP measure popularized by Eichengreen et al. [6] - often used in studies of currency crises—has been criticized, few studies have been able to come up with a feasible alternative. This study builds upon Hegerty’s [5,6] use of Principal Components Analysis (PCA) to assign weights to a set of countries’ exchange-rate depreciations, reserve losses, and interest-rate hikes. A graphical depiction, basic statistics, and the results of a set of Granger causality tests for regional spillovers show that this new measure does not provide an alternative. Results between the two measures differ too much for DPCA to be reliable without further work being done.
Generalized Impulse Response Functions, generated for VARs that use this new measure, also provide weaker evidence for international exchange-market “contagion” than had been found in earlier studies. While Latin American exchange markets appear to experience international EMP spillovers, Central and Eastern Europe (except Ukraine) and Asia do not.
It is interesting to note that Ukraine’s DPCA EMP measure closely matches its ERW measure—and that this country shows meaningful evidence of spillovers. We therefore attribute these differences to the method by which DPCA calculates these indices. These failures must be addressed for DPCA to become standard in the literature. Further research must investigate whether higher-order components might provide a more useful measure when the first dynamic principal components did not.