Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2011) Volume 4, Issue 10
Previous researches noticed that a 3D backbone structure can be mathematically represented with a 1D ? and ? dihedral angle array. However, performance of the backbone dihedral angle alignment was not supported with sufficiently large test sets to be quantified; i.e. only 2 pairs or 4 pairs of proteins were analyzed. Here we showed that it is more effective to accurately anticipate homology among 1891 pairs of proteins of 62 different proteases with the string of ? and ? dihedral angle array than famous 3D structural alignment tool TM-align. Gapless global alignment between protein structures was conducted to validate the effectiveness of performing structural alignment with strings of backbone torsion angles. Representation of 3D structure by 1D torsion angle strings allows local alignment, profile construction, hidden Markov models to be implemented with minor modifications and with almost no loss of speed compared with sequence alignment. By our further validation from the previous studies, the utility of backbone dihedral angle method could be more evident.
Keywords: Protein structure alignment, Backbone torsion angle, Backbone dihedral angle, One dimensional structure alignment.
Protein structure has always been a significant concern among molecular biologists because it provides intimate information regarding the function and mechanism of the given protein. This knowledge regarding proteins, which are key molecules in the biology of living organisms, can be used in a variety of ways, ranging from protein structure modeling [1,2] to structural genomics [3-5]. The number of published protein structures has increased to approximately 70 000; this increase represents the interest and perpetuating importance of the knowledge of protein structure for biological and pharmaceutical studies.
Numerous structural alignment algorithms have been published. Five of these, namely TM-align [2], FATCAT [6], CE [7], MAMMOTH [8], and TOPMATCH [9,10], were employed by RCSB as structure alignment service tools (www.rcsb.org). All of these algorithms are similar in their using three-dimensional (3D) coordinates of atoms. Structural alignments that mainly use 3D coordinates take much more time than do sequence alignments, which align 1D sequence strings. Whole genomes of human and mouse can be aligned in approximately 38 days with 100 machines using a well-known sequence alignment tool, BLAST [11,12]. If 3D structure coordinates can be transformed into a 1D vector, whole proteomes of human and mouse could be aligned within 1 day with a rapidity similar to that of BLAST analysis with a single computing machine because the proteome is many times smaller than the genome.
Recently, there were numerous attempts to utilize the representation of 3D protein structures into 1D structural alphabets mainly based on local oligo-peptide structures, which showed comparable performance to 3D information based approaches [13-17]. Karpen and colleagues [18] and Miao and colleagues [19] noticed that a 3D backbone structure can be mathematically represented with a 1D φ and ψ dihedral angle. In addition, it is widely accepted that backbone structural information can be used for structural alignment validation with fair credibility. For example, the widely accepted algorithm TM-align uses only alpha carbon atom coordinates [2]. The notion of Karpen et al. [18] and Miao et al. [19] may thus be plausible to be implemented to compare structural similarity between proteins with reliable credibility using fast 1D alignment algorithms.
The utilization of a reduced dimensional quantity for structural alignment using dynamic programming algorithms was previously attempted by Rose and Eisenmenger [20]. Although Rose and Eisenmenger remarked that torsion angles might be useful for structural alignment based on the Needleman-Wunsch dynamic programming algorithm, they used differential geometry [21-24] of protein chains instead. This differential geometry is more complicated to derive from 3D coordinates than φ and ψ angle values, and its superiority of accuracy and performance is doubtful. Sklener et al. [25] also attempted to represent the helical status of the backbone structure using atom coordinates of protein backbones, but they didn’t use the φ and ψ dihedral information to represent the backbone structure. Recently, YAKUSA [26] used 1D α angle arrays to reduce the dimension of the comparing information for fast structural alignment with BLAST-like algorithm. SHEBA [27] uses 1D “environmental profiles” containing information about sequence homology and residue-dependent information such as solvent accessibility, hydrogen bonds, and sidechain packing as initial alignment, which is then refined for threedimensional geometry by dynamic programming [28].
Karpen and colleagues [18] showed RMSD of φ and ψ dihedral angles (Δt) between pairs of substructure fragments of two proteins correlates with the RMSD of 3D coordinates (Δr) of the backbone atoms from the alignment using the method of Kabsch [29,30]. Recently, Miao and colleagues [19] also showed the higher coverage of local structure alignment based on backbone dihedral angles (φ and ψ angles) with Smith-Waterman dynamic programming algorithm than SSM [31], DALI [32], and CE [7] with reliable validity proven by the alignment of several of the most challenging pairs of proteins among the 68 pairs presented by Fischer and colleagues [33] and phylogenetic analysis of class II aminoacyl-tRNA synthetases.
These two researches, however, didn’t support enough size of test materials for the quantifiable evaluation of the effectiveness of backbone torsion angle alignment algorithm. Karpen and colleagues proved the reliability of their method from the case study of two proteins (i.e. ribonuclease A and the first 124 residues of actinidin) [18]. TALI of Miao and colleagues only used four pairs of proteins (i.e. 1cewI-1molA, 1cewI-1r4cA, 1hngB-1a64A, and 1nj8D-1b76A) [19]. It would be, therefore, a worth attempt to evaluate the accuracy and effectiveness of the structural alignment based on the backbone dihedral angles with large enough test sets, considering the utility of their 1D representation of structural information.
The present study attempted to evaluate the accuracy of the structural alignment with strings of backbone torsion angles using a 1D comparison algorithm by observing the correctness of the classification of homology among 1891 pairs of proteins from three kinds of 62 proteases. Phylogenetic clusterings of 62 proteases were also analyzed for the validation of this approach. Simple gapless global alignment was conducted to evaluate the appropriateness of backbone dihedral angle method. We used simple geometrical and statistical similarity measurements applying simple arithmetic operations to the angle difference to determine the degree of structural identity.
Phylogenetic and homologic analyses were conducted to test the validity of backbone dihedral angle method. Sequential and structural information of 62 proteases with intermingled homologous groups were used. Detailed descriptions of these proteases are in the following section. Sequence alignment, TM-align, and two backbone dihedral angle difference measurement methods were used to build phylogenetic trees, which might reflect different levels of accuracy by different clustering patterns.
The accuracies of homology delineation of dihedral angle method and that of TM-align were measured and compared after setting optimal thresholds. The performance was measured by ROC values, accuracy (ACC), balanced error rate (BER), the Matthews correlations coefficient (MCC), and other quantities, while the sensitivity and specificity were displayed with TP vs. FP and TN vs. FN plots and an ROC plot. The details of the experimental settings and preparation of materials follow.
Definition of φ and ψ angles
The φ dihedral angle of the ith amino acid is defined as the torsion angle of Ci-1-Ni-Cαi-Ci, and the ψ dihedral angle of the ith amino acid is defined as the torsion angle of Ni-Cαi-Ci-Ni+1. Similarly, we can define angle ω as the torsion angle of Cαi-Ci-Ni+1-Cαi+1. We assumed ω to be 180° because it is usually close to 180° with a minor exception of 0° due to the partial double bond charactRamachandran plot RMSD (RamRMSD)er. Relative 3D backbone atom coordinates can be accurately determined by simple mathematics using these three angles. The program used to calculate dihedral angles from PDB files was written in JAVA.
Ramachandran plot RMSD (RamRMSD)
We used the Ramachandran plot RMSD (RamRMSD) as the quantity that represents structural similarity based on φ and ψ angles. Similar measurement was used by Karpen and colleagues as Δt [18]. It is natural to use the RMSD of points on the Ramachandran plot as a parameter indicating structural similarity because we used φ and ψ angle information for comparison. We calculated RMSD of the Euclidean distance of every two points of matched residues on each of the two Ramachandran plots. The Euclidean distance can be defined as follows:
D = (Δφ2 + Δψ2)1/2
where D is the distance and
Δφ2 = (φ1-φ2)2, if (φ1-φ2)2 ≤ 1802
(360-|φ1-φ2|)2, if (φ1-φ2)2 > 1802
Δψ2 = (ψ1-ψ2)2, if (ψ1-ψ2)2 ≤ 1802
(360-|ψ1-ψ2|)2, if (ψ1-ψ2)2 > 1802
where φ1 and φ2 are φ angles from each residue, and ψ1 and ψ2 are ψ angles from each residue. Conditional terms are added to find the smallest distance between any two angles with our -180° to +180° notation; i.e., not to consider the distance of two angles, +180° and -180°, as 360° apart rather than 0° apart, for example. The RamRMSD would be as follows:
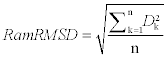
where n is the total number of residues to be compared, and Dk is the distance of points of kth residues of each protein on each Ramachandran plot as defined above.
Statistical similarity measurement with weight imposition
Although RMSD is a common measure of structural similarity, it is weak to small number of local deviations [2]. To circumvent the problems of RMSD, TM-score was used with the Levitt-Gerstein weight factor [34], which weighs close residue pairs more than distant residues. Here, we defined logPr, which weighs smaller differences, to suggest a possible substitution for RamRMSD, which is vulnerable to local deviations. We defined the probability value (Pr-value) as the probability of finding closer angular similarity than observed similarity in a random environment for each torsion angle pair of compared polypeptide chains, and used logPr (base 10) as our additional informing quantity to RamRMSD; we used Pr rather than P to avoid confusion with the hydrophobicity descriptor logP [35] or with the P-value for evaluating statistical significance of homology from null hypothesis distribution [8,11].
If the difference of the φ and ψ angles is defined as a vector Ω (ωφ1, ωψ1, ωφ2, ωψ2, … , ωφn, ωψn), where ωφk is the difference of 2 φ angles of the kth amino acid of each n-residue-long string and ωφk is the difference of 2 ψ angles of the kth amino acid of each n-residue-long string, the constant probability density function ρ(ω) and the Pr-value in a random environment can be mathematically written as follows:
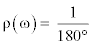
where ω is the angular difference, and

where n is the number of total residues being compared and every angular difference is presumed to be statistically independent. The uniform p.d.f. could be heuristically adjusted using observations from non-homologous alignment data of large enough sizes in further studies. Naturally, if the Pr-value is small, the structural similarity between two proteins is higher. Because multiplied values range from 0 to 1, the Pr-value is more strongly dependent for small values than for large values. A 180° difference has no effect on the Pr-value because the multiplied value is 1, but a 0° difference has a critical influence on the Pr-value because it immediately changes it to 0. We heuristically assumed that the absolute 0° difference was 1.0 × 10-8 for practical reasons; this was the highest accuracy possible based on the format of our dihedral angle data file.
Although the Pr-value is the original descriptor of the significance of similarity, we used the logPr-value to circumvent a computational overflow problem. We used log base 10 for easy comprehension of the order of magnitude of the probability, Pr.
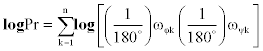
If the logPr-value is smaller, then they are more similar. The logPrvalue of a single residue ranges from -16 to 0. For global alignment, we should normalize the difference in compared amino acid residue lengths. We divided the logPr-value with residue number n and calculated the average:
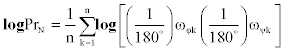
where N denotes a normalized value. A normalized logPr signifies the average logged probability of finding closer alignment between all residue-pairs compared in a random environment.
Alignment algorithm
We employed a simple alignment algorithm for single-chain proteins. Using the shorter chain as a probe on the template of the longer chain, we moved the probe chain by one residue for each calculation. The probe chain’s N-terminus began probing from the template chain’s N-terminus. When the C-terminal region of the probe passed through the C-terminus of the template, the probe’s protruding C-terminal region was compared to the N-terminal area of the template chain according to the boundary conditions. That is, where n1 and n2 are the lengths of the polypeptide chains S1 and S2, respectively, and n1< n2, where Sk(0), Sk(1), …, Sk(nk-1) denote from the first to the last amino acid residues of Sk(k=1, 2), the calculation of values (logPr and RamRMSD) should be as follows:
for(int i=0; i
for(int j=0; j
if(i+j≥n2) CalculateValue(S1(j), S2(i+j-n2))
else if(i+j
}}
During the probing, the calculated Pr-value and RamRMSD were recorded and the alignment frame that yielded the best value was selected. The best alignment frame between the logPr- and RamRMSDbased methods may differ. The alignment program was written in JAVA.
Parameter settings for alignments and clustering
Global alignment with a gap open penalty of 13, extension penalty of 3, and free end gap penalty was conducted for sequences of 62 proteases. A UPGMA algorithm with bootstrapping of 100 replicates was used for tree construction from sequence of proteases. CLC bioinformatics workbench was used for alignment and tree calculation and Geneious workbench was used for graphical representation. (8+logPr), RamRMSD, and (1−TM-score) were used for distance, and a Fitch-Margoliash algorithm was employed for building trees from protein structures. TM-score was normalized by the size of the target protein of the comparison pair. An appropriate integer (8) was added to logPr to make distances positive. Trees were generated from a distance matrix using the FITCH program of the PHYLIP package. Geneious workbench was used for graphical representation of trees.
Performance-evaluating quantities
Quantities used to evaluate the performance of the four methods (logPr and RamRMSD of backbone dihedral angle method and RMSD and TM-score measurements of TM-align) were defined as follows [36]: we considered clustering between the same type of proteases as true, and that between different types of proteases as false. There were 656 true pairs and 1235 false pairs. After setting an appropriate threshold for delineation of positive and negative classes, we defined true positive (TP), true negative (TN), false positive (FP), and false negative (FN). From these, we calculated the true positive rate (TPR), or sensitivity, and the true negative rate (TNR), or specificity; these were defined as:

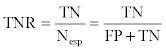
where Pexp and Nexp were the numbers of true and false pairs, respectively. The positive predictive value (PPV) and negative predictive value (NPV) were defined as follows:
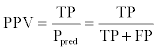
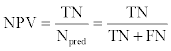
where Ppred and Npred were the number of positive and negative pairs. ACC and BER were also calculated and were defined as follows:
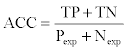

where 1-TPR was the false positive rate (FPR) and 1-TNR was the false negative rate (FNR), which were defined as:
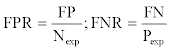
The MCC[37] was also calculated and was defined as follows:
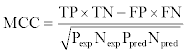
After choosing a threshold for positive and negative class delineation referring to the above quantities from various thresholds, we calculated ROC100, ROC200, ROC300, and ROC350 values to assess the ranking quality of each method. ROC values were defined as follows [38]:
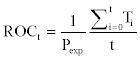
where Ti was the number of true positives ranked ahead of the ith false positive. ROC curves were drawn and AUROC for each of the four methods were calculated from specificity and sensitivity values of various thresholds.
Test set preparation
Although SCOP [39] and CATH [40] classifications are often used as references for the evaluation of alignment quality, some argue that these classifications are so discrete that detailed alignment quality might not be properly assessed [2]. In addition, databases such as CATH use other structure alignment tools for classification [2], and significant structural similarity has been shown to exist in proteins belonging to different classes [2,41,42]. Thus, we used functional classification of proteins as our classification reference, focusing more on the practical utility of the backbone torsion angle based structure alignment algorithm to correctly annotate functions of unknown proteins.
We used PDB files of 62 peptidase proteins with 20 serine-type peptidases (GO ID: 8236), 30 metallopeptidases (GO ID: 8238), 7 cysteine-type peptidases (GO ID: 8234), and 5 aspartic-type peptidases (GO: 70001). We chose the peptidase family mainly for its amenable size and the number of subgroups. Detailed descriptions of peptidases are listed in Table S1. We selected single-chain proteins without any missing residues. We neglected structures only with alpha carbon coordinates and with modified amino acids whose order of backbone atom coordinates were inverted. Fragmented structures, which compose only a partial portion of the whole protein, were also omitted while selecting proteases. The search tools of the RCSB webpage and JAVA codes were used for searching and selecting PDB files for test set preparation.
Sequence and structure trees of different groups of proteases
The structure of a protein is known to have more intimate relationship to its function than does its sequence. If φ and ψ angle alignment is reliable, the pair-wise alignment results should be accurate and the tree built from these alignment distances should be appropriate. We derived phylogenetic trees from proteins with intermingled members of various functional homologies using global alignment of backbone dihedral angles (φ and ψ angle). A total of 62 protein structures of different peptidases as described in the Materials and Methods section were used to construct phylogenetic trees (Figure 1). Distances of structure alignments were measured as described in Materials and Methods. Overall correctness could be partly assumed by the strength of clustering of proteins of the same groups without any heterologous interruptions, although strict evaluation of the pairwise distances may have differed from the aggregation of leaf nodes depending on the branching patterns.
Figure 1: Phylogenetic Trees of Different Types of Proteases: Phylogenetic trees of different proteases were built from sequence analysis(a) and structure analyses including backbone dihedral angle structure alignment method(b,c) and TM-align (d). Sequence alignment generated rather obscure clustering between serine-type proteases (yellow dots) and metalloproteases (purple dots). Aspartic-type proteases and cysteine-type proteases were dotted with cyan and red color each. Trees with our new approach showed better clustering than that of seqeunce method as explained in the text. logPr tree showed slightly better clustering than RamRMSD tree, showing weight imposition on closer similarity can improve errors of RMSD. Our two trees(b,c) showed comparable accuracy of clustering with the tree from TM-score of TM-align(d).
The clustering of structure alignment-based trees using backbone dihedral angle methods of RamRMSD (Figure 2b) and logPr-value (Figure 2c) showed clustering with accuracy comparable to that of TM-align (Figure 2d) and better than that of the sequence alignment tree (Figure 2a). Structure-based trees showed overall concrete distributions of the same homologous group members, while sequencebased trees showed stronger dispersion of serine-type peptidases and metallopeptidases.
Figure 2: Performance Displayed by TP vs. FP and TN vs. FN plot: Curves tilted to upper left indicates better accuracy. In TP vs. FP plot(a), backbone dihedral angle methods (logPr and RamRMSD) showed comparable performance to TM-align methods, performing worse for clearer cases but better for more obscure cases. In TN vs. FN plot(b), our methods showed better performance than TM-align methods for all the cases. Dashed lines signifies error rates.
A maximum of 14 metallopeptidases were posed next to each other without any interruption of other peptidases in our logPr tree, and a maximum of 9 metallopeptidases were posed next to each other in the RamRMSD tree. TM-align also showed a maximum of 14 metallopeptidases right next to each other without any heterologous interruption. Sequence-based clustering showed a stronger dispersion of metallopeptidases; a maximum of only six metallopeptidases were clustered together. A maximum of nine serine-type peptidases were posed next to each other in TM-align without any interruption, and six were posed next to each other in both of logPr and RamRMSD methods. Sequence-based clustering showed only five serine-type peptidases posed next to each other.
All four methods showed similar clustering among aspartic-type peptidases and cysteine-type peptidases. Omega-amino acid-pyruvate aminotransferase (3a8u) and protein disulfide-isomerase A3 (2alb) of cysteine-type peptidases and hydrogenase 3 maturation protease (2i8l) of aspartic-type peptidases were diverged from the others. Five lactoferins of serine-type peptidases (1b1x, 1ce2, 1i6q, 1lcf, and 1lct) were clustered very closely to each other by all four methods.
Internodes of trees from structural alignments, especially the two trees from backbone dihedral angle methods, showed relatively closer positions to the root compared to the length from leaf nodes to internodes. A comparatively shorter length from internode to root indicated that the structural information was rather discrete compared to the sequence information. This made the difference between different groups of proteins comparatively smaller than the difference between any two proteins. The small difference between the distances from leaf to root and from leaf to internode implies that a delicate setting of cutoff values would be required for accurate delineation of different homologous group members using structure alignments. This also signifies that structural information that can be employed as characters for clustering is only a small fraction of the total structural information. It is probable that concentrating on the more representative characters, thus discarding the background difference, would yield better results.
Comparison of backbone torsion angle-based method and TM-align
The trees (Figure 1) of 62 proteases were drawn based on the alignment distances of 1891 pairs. Trees drawn with backbone dihedral alignment methods showed reliable results as explained above (Figure 1b, 1c). However, quantification of the accuracy of dihedral angle method and comparison of this accuracy with other methods is still necessary. Based on our analysis, φ and ψ dihedral angle method showed reliable and even better performance. Among the 1891 pairs of proteins from 62 proteases, protein pairs with the same type of proteases were regarded as true pairs, and pairs with different types of proteases were regarded as false pairs.
The thresholds of each of the four methods to delimit true pairs and false pairs varied from the values that approximately yielded the maximum sensitivity (1.00) and minimum specificity (0.00) to the values that approximately yielded the minimum sensitivity (0.00) and maximum specificity (1.00). An increase in sensitivity generally induced a decrease in specificity during the change of the threshold value. For a proper comparison between methods, we selected the optimum threshold value as that which showed both sensitivity (TPR) and specificity (TNR) of more than 0.5 for TM-align and 0.6 for φ and ψ dihedral angle method with the highest MCC. MCC was used instead of ACC because this test set is imbalanced, having approximately twice as many false pairs as true pairs [43,44]. We applied different criteria for the threshold because TM-align could not show both TPR and TNR of more than 0.6 at the same time. log(1/45) for logPr, π/1.9375 for RamRMSD, 5.5 Å for RMSD of TM-align, and 0.285 for TM-score were chosen as optimal thresholds.
φ and ψ dihedral angle methods showed performances comparable to those of TM-align based on the results of these selected thresholds (Table 1). The sensitivity (TPR) and specificity (TNR) of φ and ψ dihedral angle methods were above 0.6 as selection criteria. Sensitivities of the methods ranged from 0.62 of logPr and 0.64 of RamRMSD to 0.50 of RMSD of TM-align and 0.52 of TM-score. Specificity was the highest at 0.68 in TM-align RMSD and the lowest at 0.53 in TM-score, while logPr showed a specificity of 0.66 and RamRMSD showed a specificity of 0.63. Of the four methods, logPr showed the highest PPV (0.49), the highest NPV (0.77), the highest ACC (0.65), the lowest BER (0.36), and the highest MCC (0.27), while TM-score showed the lowest PPV (0.37), the lowest NPV (0.67), the lowest ACC (0.52), the highest BER (0.48), and the lowest MCC (0.04). RamRMSD showed similar values to those of logPr for PPV (0.48), NPV (0.77), ACC (0.63), BER (0.36), and MCC (0.26). TM-align RMSD showed similar performance to that of logPr and RamRMSD with a PPV of 0.45, NPV of 0.72, ACC of 0.62, BER of 0.41, and MCC of 0.18.
| Methods | TPR | TNR | PPV | NPV | ACC | BER | MCC |
|---|---|---|---|---|---|---|---|
| logPr | 0.62 | 0.66 | 0.49 | 0.77 | 0.65 | 0.36 | 0.27 |
| RamRMSD | 0.64 | 0.63 | 0.48 | 0.77 | 0.63 | 0.36 | 0.26 |
| TM-RMSD | 0.50 | 0.68 | 0.45 | 0.72 | 0.62 | 0.41 | 0.18 |
| TM-score | 0.52 | 0.53 | 0.37 | 0.67 | 0.52 | 0.48 | 0.04 |
Table 1: Performance of the Four Methods.
The overall performance of backbone dihedral angle approach was quite valid compared to that of TM-align, both with logPr and RamRMSD measurements, regarding the above statistics. We further investigated the quality of prediction using ROC100, ROC200, ROC300, and ROC350 values, where a higher ROC value signifies better quality. The values are displayed in Table 2. TM-align RMSD showed the highest ROC100 (0.204), the second highest ROC200 (0.246), and the third highest ROC300 (0.290) and ROC350 (0.313). This signifies that TM-align RMSD was the most accurate in the range of 1st to 100th false positives, but failed to be the best in broader ranges. ROC100 (0.153, 0.149) of logPr and RamRMSD were both less than the ROC100 of TMalign RMSD (0.204) and TM-score (0.193). However, ROC200 (0.251) of logPr and ROC300 (0.324, 0.304) and ROC350 (0.354, 0.336) of logPr and RamRMSD were higher than the best values of the TM-align methods.
| Methods | ROC100 | ROC200 | ROC300 | ROC350 |
|---|---|---|---|---|
| logPr | 0.153 | 0.251 | 0.324 | 0.354 |
| RamRMSD | 0.149 | 0.229 | 0.304 | 0.336 |
| TM-RMSD | 0.204 | 0.246 | 0.290 | 0.313 |
| TM-score | 0.193 | 0.241 | 0.277 | 0.293 |
Our logPr and RamRMSD showed worse performance for the clearer cases (protein pairs before 100th false positives) but showed comparable accuracy for more difficult cases (protein pairs after 100th false positives) as can be seen by high ROC300 and ROC350 values.
Table 2: ROC values of the Four Methods.
To further evaluate the sensitivity and the quality of the prediction represented with ROC values, we drew a classical chart of TP versus FP [45] (Figure 2a). As can be seen in Figure 2a, TM-score and RMSD of TM-align showed better performances in the region from the 1st to approximately the 100th false positive. However, RamRMSD and logPr performed better in the region of the 100th false positive or more. The worse performances of backbone dihedral angle method in the top 100 positive guesses indicates that backbone torsion angle-based anticipations are less robust than TM-align in clearer cases.
We also analyzed the accuracy of negative anticipation. Figure 2b shows the number of true negatives along with the increase in the number of false negatives. Backbone dihedral angle method, using both logPr and RamRMSD measurements, showed more valid performances than TM-align methods in all ranges. logPr and RamRMSD showed similar performances with a slightly better performance of logPr. To further analyze performance, we graphed the ROC curves of the four methods using specificity and sensitivity values observed at various thresholds (Figure 3). The performances of our two methods (with areas under the ROC curve [AUROCs] of 0.6743 [logPr] and 0.6694 [RamRMSD]) were comparable to those of TM-align RMSD and TMscore (with AUROCs of 0.5965 and 0.5494, respectively).
Backbone dihedral angle methods showed comparable performances, and in some cases outperformed, when delineating the functional homology of the 62 proteases, as shown by the high ACC, BER, MCC, and ROC values. The chart of TP vs. FP and TN vs. FN (Figure 2) also demonstrate the comparable performances of this approach. The ROC curve (Figure 3) and high AUROC values also support the validity of our new method.
Weighted dihedral angle method (logPr) showed improvement over RamRMSD. However, in this set of 1891 pairs of 62 proteases, the Levitt-Gerstein weight factor [34] -exploited TM-score performed worse than did non-weighted TM-align RMSD, especially in the obscure cases of delineation pairs, which is shown in Figures 2a, 2b, and 3. TMalign aligns two proteins with TM-score-based heuristic iterations and uses RMSD only as an optional quantity; i.e., the different performance only depends on the application of the weight factor to the distances of the aligned residues. This implies that weighting of closer similarity based on 3D coordinates might mislead the delineation of homology in difficult pairs, indicating that local deviations might be important information in less significant cases. Weighting on closer backbone torsion angle similarity, however, did not distort the appropriate alignment, as can be seen by the high performance measurements in Tables 1 and 2 and in the sensitivity (Figure 2a), specificity (Figure 2b), and ROC curve (Figure 3) graphs, signifying that distance based on backbone torsion angle information is more robust for comparison than that based on 3D information.
Backbone dihedral angle approach showed reliable accuracy compared to sequence alignment, as shown in Figure 1, and with TM-align, as shown in Figures 1–3 and Tables 1 and 2. In addition, the Spearman rank correlation coefficient and Pearson’s correlation coefficient of the pair-wise comparison from the four methods were calculated (Table 3) for further validation of backbone dihedral angle method. The correlation between our two methods of logPr and RamRMSD and TM-align RMSD (r = 0.53 and 0.55; rs = 0.45 and 0.47) was stronger than the correlation of each with TM-score (r = 0.41 and 0.44; rs = 0.13 and 0.16). The rather solid correlation of TM-align RMSD and TM-score with backbone dihedral angle methods partly indicates the validity of our new approach. Backbone torsion angle method showed very high correlation between the two measurements (logPr and RamRMSD) based on both the Pearson’s (0.95) and Spearman’s rank correlation coefficients (0.92), higher than those between TMalign RMSD and TM-score (r = 0.56 and rs = 0.33).
| logPr | RamRMSD | TM-RMSD | TM-score† | |||||
|---|---|---|---|---|---|---|---|---|
| r | rs | r | rs | r | rs | r | rs | |
| logPr | 1 | 1 | 0.95 | 0.92 | 0.53 | 0.45 | 0.41 | 0.13 |
| RamRMSD | 0.95 | 0.92 | 1 | 1 | 0.55 | 0.47 | 0.44 | 0.16 |
| TM-RMSD | 0.53 | 0.45 | 0.55 | 0.47 | 1 | 1 | 0.56 | 0.33 |
| TM-score | 0.41 | 0.13 | 0.44 | 0.16 | 0.56 | 0.33 | 1 | 1 |
†We inverted the sign of TM-score values because TM-score scores closer distance with higher TM-score making the correlation with others negative.
r: Pearson’s correlation coefficient
rs: Spearman’s rank correlation coefficient
Table 3: Pearson and Spearman Correlation Coefficients.
Computational time and complexity
The computational complexity of alignments could be reduced to O(nm) with pre-calculated dihedral angle arrays from O(m2n2) of typical 3D coordinate-based alignments, where m and n is the length of the compared proteins. Computation time of backbone dihedral angle methods was calculated and drawn (Figure 4). Both the logPr and RamRMSD methods showed linear relationships with R2 of 0.83 (logPr) and 0.69 (RamRMSD), with the search space calculated by multiplying the lengths of each peptide chain of the pair-wise comparison. The logPr method took slightly more time than RamRMSD. The mean and median CPU times of 94.42 and 90 ms each for logPr and 79.14 and 80 ms each for RamRMSD were needed to calculate a pair of proteins among the 1891 pair-wise comparisons with 3.0 GHz AMD phenome processor on an openSUSE 11.2 platform. TM-align took an average CPU time of 754.30 ms to calculate one pair of comparisons in the same environment.
Although backbone dihedral angle method was approximately 8-fold (logPr) or 10-fold (RamRMSD) faster on average, TM-align tended to be much slower when the size of the compared protein pair increased. For example, the pair with the largest search space of 809568 (res.2), 1Q2L (939 res.), and 2GTQ (867 res.) consumed only 220.0 ms (logPr) and 130.0 ms (RamRMSD) using backbone dihedral angle methods, but took 9160 ms with TM-align, which is approximately 40 times slower than logPr and approximately 70 times slower than RamRMSD. Considering that our JAVA program needed an interpreter (JVM) to perform the calculation, the rapidity of backbone dihedral angle algorithm might be more than proved here. Applying more sophisticated sequence alignment algorithm, however, would consume more computational resource than this simple performance evaluating algorithm. The average and median values of the search space were 2.98 × 105 and 1.38 × 105 (residue2).
Backbone dihedral angle approach is reliable based on the results from 1891 pairs of proteins as presented herein. BLAST and other methods can be applied with minor modifications as shown by the case of YAKUSA [26] with comparable rapidity as sequence alignment by changing the 3D backbone structure to 1D torsion angle strings. Though the rapidity and validity of the backbone dihedral angles approach is comparable and even better for more obscure comparisons than famous 3D alignment TM-align as shown here with 1891 test protein pairs, this approach’s robust performance is currently not very much appreciated.
This method could also be further enhanced by, for example, cumulating φ, ψ, and ω angles for exact backbone structure matches to improve accuracy. Future studies might consider investigating the use of numerous possible weighting schemes. Regarding the validity of backbone dihedral angle alignment in structure comparison proven here and its simplicity which can be further exploited, we are hopeful that this approach could be used as a reliable basis in structure related protein researches.
We thank the support from the Brain Korea 21 Project of Ministry of Education, Science, and Technology of South Korea in 2011.