Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2017) Volume 7, Issue 1
In this paper, an effort has been made to study the isotope coefficient in high TC Superconductors by using the variation of isotopic coefficient with the number of CuO2 layers and the variation of isotope coefficients on transition temperature TC . The Hamiltonian for CuO2 layers using BCS type model and extra term of interlayer interaction between CuO2 layers has been considered. Expressions for isotope effect (α) and transition temperature (TC) are obtained and numerically calculated for experimental values by using Green’s function technique.
<Keywords: Isotope effect; CuO2 layers; Isotope coefficient; High TC superconductors
After the discovery of high TC cuprate superconductors in 1986 [1] at 35 K, the field is buzzing with research activities. Efforts to increase the transition temperature are currently going on. Till now the highest reached TC under pressure is 164 K in HgBa2Ca2Cu3O8+8 [2]. These cuprates have unconventional properties both in normal and superconducting state [3,4]. Till date there is no consensus on the origin of pairing mechanism. It is now widely suggested that spin fluctuation driven pairing mechanism provides a good agreement between theory and experiments [5]. However, there are several experimental observations which clearly indicate that this purely electronic picture is incomplete and lattice effects have to be taken into account [6-8]. Isotope shift of TC is regarded as the defining signature of superconducting pairing resulting from phonons. In high TC superconductors, a small isotope effect is found [9-11]. Suppression of this effect is not explained within conventional BCS theory which predicts that the critical temperature TC and isotope mass M are related by TC ∝ M-α where α=0.5 for all elements. To explain the small isotope effect in high TC compounds, many mechanisms including resonance valence bond [12], excitons [13], Plasmon’s [14] and antiferromagnetic spin fluctuation mediated pairing are proposed [15]. Daemen and Overhauser [16] found that the existence of a short-range attraction in addition to the conventional phonon pairing interaction suppresses the isotope effect significantly at high temperatures. Here we present the variation of isotope coefficients with number of CuO2 layers and the variation of isotope coefficients on transition temperature TC [17- 22]. As the trilayer material has highest (TC) in these cuprates but it has very small isotope coefficient (α). Clearly the argument that a mechanism other than an electron phonon interaction dominates the superconductivity based only on a small (α) in a cuprate with relatively high (TC) is inappropriate. The observed CuO2 layer dependence of the isotope effect indicates that the interlayer coupling between the adjacent CuO2 planes is necessary for superconductivity in layered cuprates [23-26]. For monolayer materials having lower (TC) the interlayer coupling plays a less important role and (TC) can be mainly controlled by the phonon coupling yielding a larger size of isotope coefficient with increasing the number of CuO2 layers in a unit cell, the interlayer coupling begins to play an important role in enhancing (TC) and the isotope effect is expected to be small.
Formulation
The model Hamiltonian for our system can be described as
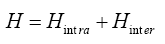
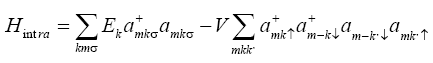
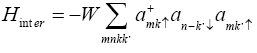
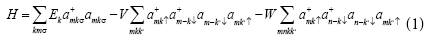
Where 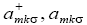 σdenote the fermions creation and annihilation operator respectively, k is the wave vector and σ is spin index for fermions.
σdenote the fermions creation and annihilation operator respectively, k is the wave vector and σ is spin index for fermions.
In our present analysis we use a Green’s function, defining as
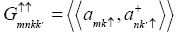 (2)
(2)
Equation of motion is written as
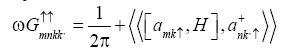
Evaluating the commutator 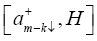 using the Hamiltonian (1) we get
using the Hamiltonian (1) we get
And writing the equation of motion as
 (3)
(3)
Putting the value of commutator  in equation (3) we get
in equation (3) we get
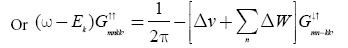 (4)
(4)
Now we introduce the order parameter Δ such as
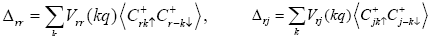
Where 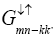 is another Green’s function which may be written as
is another Green’s function which may be written as
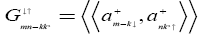 (5)
(5)
This Green’s function may also be written in terms of equation of motion as
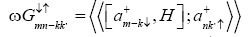 (6)
(6)
Evaluating the commutator 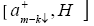 using the Hamiltonian
using the Hamiltonian
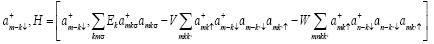
Putting the commutator 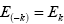 from (7) in equation (6) we get
from (7) in equation (6) we get
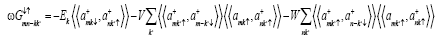
But from the law of conservation of energy
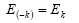
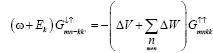 (8)
(8)
In equation (4) we finally obtained the equation
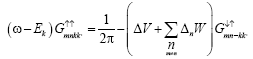 (9)
(9)
Multiply (ω+Ek) in equation (9) and putting the value of 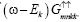 from equation (8) then we get the Green’s function
from equation (8) then we get the Green’s function 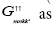
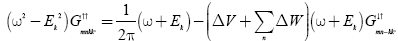 (10)
(10)
Multiplying by (ω+Ek) in the equation (8) and putting the value of 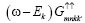 from equation (9) we get the Green’s function as
from equation (9) we get the Green’s function as
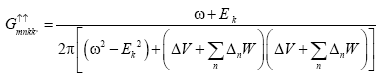
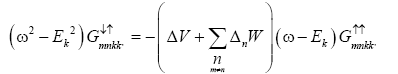
We know from equation (9)
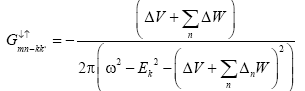 (11)
(11)
Using the Green’s function, we can obtain the expression for order parameter Δmn and correlation parameter γ the order parameter Δmn may be written as
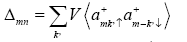 (12)
(12)
Correlation function 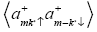 is related to Green’s function
is related to Green’s function 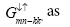
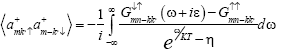 (13)
(13)
Where η=-1 for fermions, K=Boltzmann constant and T= Temperature
Green’s function 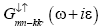 and
and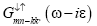 may be expressed as
may be expressed as
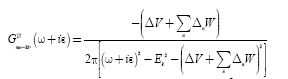 (14)
(14)
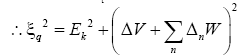
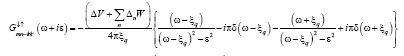 (15)
(15)
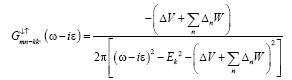 (16)
(16)
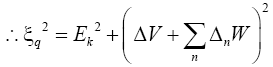
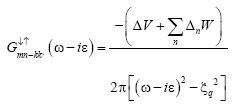
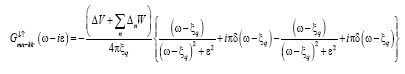 (17)
(17)
Substitute both the Green’s function 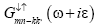 and
and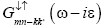 from equation (13) and then after
from equation (13) and then after
solving we get correlation function.
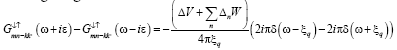 (18)
(18)
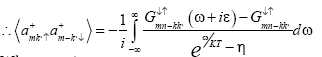
Where η=-1
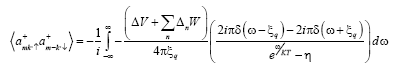
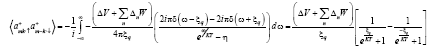
Put 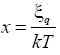
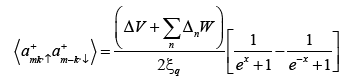 (19)
(19)
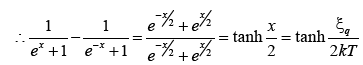 Using in (19) we get
Using in (19) we get
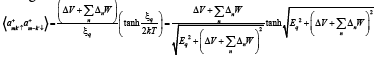 (20)
(20)
Then we can obtained the expression of or dr parameter Δir by substituting correlation function in equation (12)
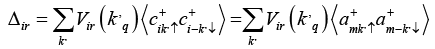
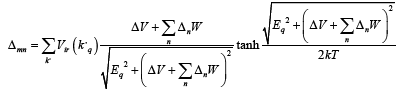
Converting summation over K into integration with cut-off energy ħωD from the Fermi level we get
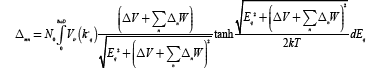 (21)
(21)
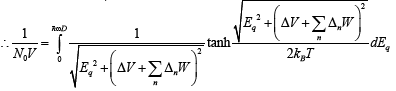 (22)
(22)
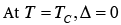
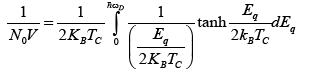 (23)
(23)
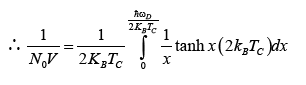
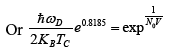
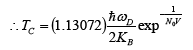 (24)
(24)
The Isotope effect coefficient is
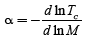 (25)
(25)
Using equation (29) and (30) we get
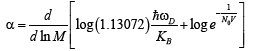 (26)
(26)
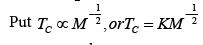
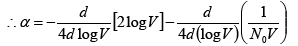 (27)
(27)
Differentiating we get
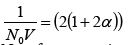 (28)
(28)
Now from equation (24) we get
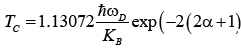 (29)
(29)
By solving equation (33), we get α as
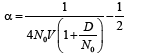 (30)
(30)
The values of α and TC are calculated from equation (29) and (30) respectively for various values of different CuO2 layers (Table 1).
| S No | α | TC | |
|---|---|---|---|
| 1 | 0.05 | 37.586 | |
| 2 | 0.1 | 30.772 | |
| 3 | 0.2 | 20.627 | |
| 4 | 0.3 | 13.827 | |
| 5 | 0.4 | 9.268 | |
| 6 | 0.5 | 6.212 | |
| 7 | 0.6 | 4.164 | |
| 8 | 0.7 | 2.791 |
Table 1: Table for values of (α) and (TC).
The numerical analysis of equation (29) and (30) have been calculated for different CuO2 layers taking 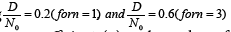 .Figure 1a is plotted between isotope coefficient (α) and number of CuO2 layers (n) per unit cell. Figure shows that as increasing number of CuO2 layers per unit cell, isotope coefficient (α) linearly decreases. For n=1, the value of (α) is 0.34 and it decreases continuously with number of CuO2 layers. At n=3, isotope coefficient (α) is 0.1317 which is very low. This systematic reduction of isotope coefficient with increasing CuO2 layers indicates that isotope effect can be negligible for multilayer cuprates. This result is good agreement with experimental result made by Chen et al. Figure 1b is plotted between transition temperature (TC) and isotope coefficient. The curve shows that as increasing (α), the transition temperature exponentially decreases so for lower isotope coefficient TC will be maximum and TC decreases for higher values of (α). So we can say that as increasing number of CuO2 layers, (α) decreases and the transition temperature increases. This result also supported by Chakravarty et al.
.Figure 1a is plotted between isotope coefficient (α) and number of CuO2 layers (n) per unit cell. Figure shows that as increasing number of CuO2 layers per unit cell, isotope coefficient (α) linearly decreases. For n=1, the value of (α) is 0.34 and it decreases continuously with number of CuO2 layers. At n=3, isotope coefficient (α) is 0.1317 which is very low. This systematic reduction of isotope coefficient with increasing CuO2 layers indicates that isotope effect can be negligible for multilayer cuprates. This result is good agreement with experimental result made by Chen et al. Figure 1b is plotted between transition temperature (TC) and isotope coefficient. The curve shows that as increasing (α), the transition temperature exponentially decreases so for lower isotope coefficient TC will be maximum and TC decreases for higher values of (α). So we can say that as increasing number of CuO2 layers, (α) decreases and the transition temperature increases. This result also supported by Chakravarty et al.
First of all Hamiltonian for CuO2 layers using BCS type model and extra term of interlayer interaction between CuO2 layers has been considered, using this equation expression for isotope effect (α) and transition temperature (TC). Expression obtained is numerically solved using Green’s function technique and then the value of isotope effect (α) and transition temperature (TC) is calculated. The graph is plotted between isotopic coefficient and number of CuO2 layers. The second graph is plotted between isotope effect (α) and transition temperature (TC). Then conclusion is drawn comparing with available experimental result. The tri layer material has highest (TC) in these cuprates but it has very small isotope coefficient (α). Clearly the argument that a mechanism other than an electron-phonon interaction dominates the superconductivity based only on a small (α) in a cuprate with relatively high (TC) is inappropriate. The observed CuO2 layer dependence of the isotope effect indicates that the interlayer coupling between the adjacent CuO2 planes is necessary for superconductivity in layered cuprates. For monolayer materials having lower (TC) the interlayer coupling plays a less important role and (TC) can be mainly controlled by the phonon coupling yielding a larger size of isotope coefficient with increasing the number of CuO2 layers in a unit cell, the interlayer coupling begins to play an important role in enhancing (TC) and the isotope effect is expected to be small.