Clusters are well suited for a rapidly increasing number of applications and they have been an active field of research for about a quarter of a century. Instead of reviewing all the literature, we refer the reader to the already existing review article by Baletto and Ferrando and also to the book by Wales [1,2]. Particularly, gold clusters are of potential relevance to the nanoelectronics industry and hence remain the subject of many experimental as well as theoretical studies. They contain edge atoms that have low coordination [3] and can adopt binding geometries that lead to a more reactive electronic structure [4]. Gold in the nanoregime, especially gold nanocrystals, have shown size-sensitive reactive properties and are considered to be as promising chemical catalysts [5]. As one of the precious metals, gold has good corrosion resistance and extremely high stability and has been widely researched for biomedical applications [6,7]. The vibrational properties of clusters and small particles have been studied very intensively, [8-15] and are vital for understanding and describing the atomic interactions in the cluster [16-21]. Thermal properties like heat capacity and thermal conductivity as well as many other material properties are strongly influenced by the vibrational density of states (VDOS). For this reason, a better understanding of the rules governing the vibrational properties of nanostructured materials is of high technological and must be given a high priority. The vibrational properties play a major role in structural stability [14,15,22]. The sizedependent properties of metallic clusters are currently of considerable interest, both experimentally [23] and theoretically [13,24]. Although the size effect on specific heat capacity has recently attracted much attention, [25] many publications only focus on low temperature [26]. Some of the theoretical studies on the thermodynamic properties of clusters are based on molecular-dynamic simulations [1] from which the caloric curve, the heat capacity of clusters and the phase transitions can be determined. Nanoclusters are interesting because their physical, optical and electronic characteristics are strongly size dependent. Often changing the size by only one atom can significantly alter the physical chemical properties of the system [27]. Reyes-Nava et al. [28] calculated the heat capacity for a few Na_N systems using the simple many-body Gupta potential, which approximates the atomic interactions with an analytical description that does not explicitly include electronic degrees of freedom. It was found that solid-liquid phase transitions occurring over a certain temperature range depend critically on the size N of the system. Accurate molecular dynamics simulations were carried out by Lee et al. [29] From a literature search, [30] one can see that only a very few theoretical studies attempt to calculate the thermodynamical properties of the clusters directly through determination of the partition function Z. Doye and Calvo calculated the partition function for Lennard-Jones clusters with N ≤ 150 [31]. In this study we combine numerical finite-difference approach and DFTB method. At T=0, the vibrational frequency of a re-optimized neutral gold cluster is obtained for optimized cluster of Au_N=3-20 which was calculated by Dong and Springborg [32]. The desired set of system eigenfrequencies (3N-6) is obtained by a diagonalization of the symmetric positive semidefinite Hessian matrix. The effect of the range of interatomic forces has been studied. We found that the lower frequencies made an excellent contribution to the heat capacity (to be able to store significant heat energy) even at low temperatures. Moreover, we have also compared our C_vib values of Au_N=14 neutral gold cluster with an anionic cluster Au_N=11-14⁻ calculated by Koskinen et al. [33,34], and we have reached the size dependency at temperature 300/950 K. In the present work, we theoretically investigated the behavior of the vibrational heat capacity of re-optimized gold cluster for size of N₁₄. The numerical approach employed allows the accuracy of the results to be increased. Our novel method, is reliable to accurately predict the physical properties of much larger clusters. In a first attempt, we applied on the mentioned gold cluster.

The DFTB [35-37] is based on the density functional theory of Hohenberg and Kohn in the formulation of Kohn and Sham. In addition, the Kohn-Sham orbitals ψi(r) of the system of interest are expanded in terms of atom-centered basis functions {?_m(r)},

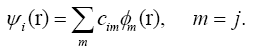(1)

While so far the variational parameters have been the real-space grid representations of the pseudo wave functions, it will now be the set of coeffcients c_im. Index m describes the atom, where ?_m is centered and it is angular as well as radially dependant. The ?_m is determined by selfconsistent DFT calculations on isolated atoms using large Slater-type basis sets. In calculating the orbital energies, we need the Hamilton matrix elements and the overlap matrix elements. The above formula gives the secular equations

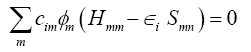(2)

Here, c_im's are expansion coeffcients, ?_i is for the single-particle energies (or where ?_i are the Kohn-Sham eigenvalues of the neutral), and the matrix elements of Hamiltonian H_mn and the overlap matrix elements S_mn are defined as

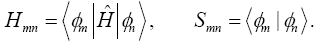(3)

They depend on the atomic positions and on a well-guessed density (r). By solving the Kohn-Sham equations in an effective one particle potential, the Hamiltonian ˆH is defined as

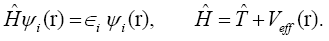(4)

To calculate the Hamiltonian matrix, the effective potential V_eff has to be approximated. Here, 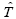being the kinetic-energy operator 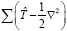and V_eff (r) being the effective Kohn-Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,

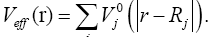(5)

is the Kohn-Sham potential of a neutral atom, r_j = r-R_j is an atomic position, and r_j being the coordinates of the j -th atom. The short-range interactions can be approximated by simple pair potentials, and the total energy of the compound of interest relative to that of the isolated atoms is then written as,

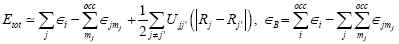(9)

Here, the majority of the binding energy (?_B) is contained in the difference between the single-particle energies ?_i of the system of interest and the single particle energies of the isolated atoms (atom index j, orbital ndex mj), is determined as the difference between ?_B and for diatomic molecules (with ESCFB being the total energy from parameter-free density functional calculations). In the present study, only the 5d and 6s electrons of the gold atoms are explicitly included, whereas the rest are treated within a frozen-core approximation [35,37,38].

Re-optimization and the force constants (FCs)

The finite-difference method has been implemented within DFTB approach for our calculation (a finite-difference approximation to calculate the numerical force constants). We found a total energy over those gradients were extended for a small displacement ds=± [0.01] au within the equilibrium coordinates of a previously optimized structure (at T=0) by Dong and Springborg [32]. However, the DFTB method has some difficulties to extract the numerical force constants which are most important for our spectrum calculations. Mainly, to get one set of hessian matrix it is necessary to compute two times (set and reset) for both positive and negative gradients. Nevertheless, the gradient ds is a reasonable value and allowed us to discriminate between the translational, rotational motion (Zero-eigenvalues) and the vibrational motion (Non-Zero-eigenvalues).

In our case, we have calculated the numerical first-order derivatives of the forces (F_iα, F_jβ) instead of the numerical-second-order derivatives of the total energy (E_tot). In principle, there is no difference, but numerically the approach of using the forces is more accurate,

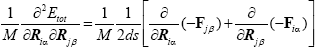(7)

Here, ds is a differentiation step-size and M represents the atomic mass, for homonuclear case. The complete list of these force constants (FCs) is called the Hessian H, which is a (3N × 3N) matrix. Here, i is the component of (x, y or z) of the force on the j' th atom, so we get 3N.

Calculation of vibrational heat capacity

Finally, from the calculated vibrational frequencies and with the use of Boltzmann statistics [39-41], we can get the formula to investigate size, structure and temperature effects on the vibrational heat capacity of clusters,

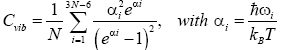(8)

Here, N is the total number of atoms in a cluster, ? is the reduced Planck's constant, ω_i is vibrational frequencies (low(min); high(max)), kB is Boltzmann's constant and T is the absolute temperature. Naturally, zero frequencies are excluded from summation (3N-6) in equation (8). In this study, we focus only on the vibrational part of the heat capacity, i.e., on C_vib.

The classical treatment of C_trans+C_rot+C_elec: The heat capacity of a system with independent degrees of freedom can be approximated as a sum of its individual contributions,

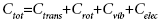(9)

Here, C_trans, C_rot, C_vib and C_elec are called as translation, rotational, vibrational and electronic heat capacity. We have proceeded to calculate the specific heat C_vib contribution due to the vibrational energy. In this study, we focus only on the vibrational part of the heat capacity, i.e., on C_vib. The other contributions are treated classically. Most often, the electronic excitation energies are much larger than kT and we neglected the electronic partition function.

Vibrational properties and low temperature heat capacity of Au_N=14 cluster

In this article, we present the low-temperature behavior of the vibrational heat capacity of gold cluster Au_N=14 at temperature range from 0.5 to 300=950 K. The desired set of system eigenfrequencies (3N- 6) for non-linear harmonic oscillator is obtained by a diagonalization of the symmetric positive semidefinite Hessian matrix. In our case, Au_N=14 has Cs symmetric structure (Figure 1) and indeed of low symmetry [32]. The vibrational spectrum in structures spans the range from 17.02 up to 240.20 cm^-1. The Au₁₄ spectrum includes several low-frequency modes. However, the frequencies are not necessarily all distinct due to degenerations state; i.e., some of the roots of the secular equation may occur more than once. The spectrums are 17.02, 18.86, 19.53, 19.75, 24.31, 25.34, 27.18, 34.04, 34.53, 38.67, 42.79, 43.21, 44.63, 58.46, 58.89, 69.39, 70.86, 84.22, 84.87, 92.74, 109.70, 113.59, 130.96, 132.76, 147.38, 152.90, 167.18, 176.74, 181.82, 182.93, 186.81, 198.47, 203.39, 215.87, 225.76 and 240.20 cm^-1. The effect of the range of interatomic forces are studied, especially, the lower frequencies because they make a larger contribution to the heat capacity. Figure 2 shows the Gaussianbroadened vibrational density of states (VDOS), obtained by centering a Gaussian function with a full width at half maximum (FWHM) of 6 cm^-1 on each of the normal mode frequencies of Au₁₄. Moreover, expectation of VDOS is weighted (self-existence) by the IR intensity and Raman activity of the various modes. Here, the frequency ranges (17.02 to 240.20 cm^-1) are within the Far Region of IR (Far Infrared FIR, IR-C), 200-10 cm^-1 and also within the Middle Region of IR (Mid Infrared MIR, IR-C), 3330-200 cm^-1. The strongest changes are visible in the low- and high-frequency parts of the spectrum. Only the relative intensities of the bands can be found. However, some bands at 19.53, 19.75, 34.04, 34.53, 58.46, 58.89 and 84.22, 84.87 cm^-1, which are doubly degenerate modes was much more pronounced and the rests of the 28 bands are non-degenerate modes. We see that both the shape and structure disordering influences the vibrational spectrum and, therefore, heat capacity according to equation (8) shown in Figure 3. Vibrational frequencies decrease (soften) as asymmetry and disorder of nanoparticles increase. By determining the vibrational modes, the question of local stability of a cluster is addressed. The lowest, is a bending mode vibration and may be highly an harmonic. A useful feature of this method is that, if once the vibrational modes are determined, then there is even possibility to obtain the Raman and IR intensities. In Figure 3, we show the heat capacity C_vib as a function of T, for N=14 cluster size. As shown by this Figure, at very low temperatures (T → 1.75-0.5 K) the C_vib curve falls off to zero. Surprisingly, at lower temperatures (1.75-0.5 K) the value of C_vib is very small and close to zero. This shows that some of the modes of vibration of the cluster are frequencies which cannot be accessed at low temperatures. Moreover, the interatomic vibrations in heat capacity can be neglected at around (1.75-0.5 K) and the C_vib curve rises gradually with temperature, which is an exact signature of the vibrational changes. The smooth change, especially pronounced at low temperatures (1.75-25 K), is even more interesting. It is due to the energy increase of the system. For a given size, the reduction of the heat capacity is more significant at lower temperatures. As the temperature is raised, the difference between the vibrational energies becomes progressively more conspicuous. There can never be any method which explains the difference as long as we retain a simple harmonic oscillator. However, the C_vib curve gives a confirmation that is temperature dependent. In the quantum limit, T(1.75-0.5 K) → 0, the C_vib curve approaches zero, while in the classical limit, T( ? 300/950 K) → high temperature → size effect, the curve moves towards a value of C_vib=2.50/2.57 k_B/atom, which clearly indicates a temperature influenced size effect/dependency.

Figure 1: The global optimum structure of Au₁₄(Cs) at T=0 K.

Figure 2: VDOS of re-optimized gold cluster Au₁₄ at T=0 K. X-axis: atomic units; Y-axis: Degree of Degeneracy. The X-axis in terms of wavenumbers: 17.02 to 240.20 cm^-1) (1 au=27.211396 eV=219474.6305 cm^-1).

Figure 3: Au_N (N=14): C_vib per atom as a function of temperature at 0.5-300 K. α_i=ω_i/(0.6950356*T) of eqn. (8).

Comparisons

Koskinen et al. [33] studied the fundamental question of the thermodynamic stability of low-dimensional nanostructures. They investigated the dynamics of the liquid phase and the solidification transition of gold clusters anions from Au₁₁⁻ to Au₁₄⁻ using a recently established charge self-consistent density functional based tightbinding (DFTB) model for gold [34]. To be noticed that Koskinen et al. were exploring melting properties in their research perhaps due to the existence of the isomers. We may consider that all our trends are affected by this `uncontrolled parameter' of charge-state (for example, the processes involving changes in the charge state of interacting particles). For Au clusters, Koskinen et al. [33] calculated above the ground states of N=11, 12, 13, and 14, respectively, corresponding roughly to T=1000 K. Particularly, they have shown Au₁₄⁻ as an example to demonstrate the features of a novel liquid-liquid coexistence (LLC), for Au₁₄⁻ the LLC ends at E_tot ~ 2 eV followed by a 3D-liquid-3D-solid coexistence for E_tot<1.1 eV corresponding roughly to temperatures around 300 K (Figure 3c) for the partial caloric curves T(E_tot) of both dimensionalities [33]. The planar clusters form the hot, low-potential energy phase. The 3D liquid phase has the heat capacity of C_vib=4.05 kB and the 3D solid phase C_vib=3.06 kB per atom, which are greater than our estimated value C_vib=2.50 k_B/atom at 300 K, for neutral cluster Au₁₄. Moreover, the expected absolute value C_vib should be 2.57 k_B/atom. In our case, the difference is only 0.07 k_B/atom which is reasonable within the numerical accuracy. Nevertheless, C_vib has been achieved almost an accurate value, 2.56(389) k_B/atom when the temperature is high enough, 950 K. But in the Koskinen et al. [33] case, the differences were higher 1.48 and 0.49 k_B/atom than the expected absolute value for both 3D liquid and 3D solid phases. This discrepancy is due to the minimum energy difference of the anionic [33] and neutral clusters (which are more stable) [32]. So we conclude that the 2D planner structure is preferential over the 3D Structure. For the study of melting mechanisms, one ultimately has to consider isomer structures, which are energetically close to the minimum structure (ΔE~kT). In our study, the electronic degrees of freedom do not enter the partition function. Instead, we rely on the assumption that the electronic excitation energies are much larger than kT.

The boson peak C_vib/T³ vs T: As shown in Figure 4, with respect to the equation (8) and the corresponding Boson peak C_vib/T³ vs T were plotted at temperature within the range T=0.5-100 K. First, we are surprised by our observation of a Boson peak in our nanoparticles. Zhang and Douglas [42,43] usually study the Boson peak from the velocity autocorrelation function, but they are both concerned about an “excess” contribution to the vibrational density of states. This feature has been observed in metal nanoparticles and zeolites (see: Greaves) and attributed to the coordinated harmonic motions of groups of atoms in the boundary region of the particle. There are similarities here to a glass because the surface of a nanoparticle has many features in common with this class of materials. In cases where the modes have been resolved, the Boson peak has corresponded to a ring of oscillating particles, the relatively low mass being related to the relatively high mass of these modes. Farrusseng and Tuel [44] also studied the perspectives on zeolite encapsulated metal nanoparticles and their applications in catalysis. One of the universal features of disordered glasses is the “Boson peak”, which is observed in neutron and Raman scattering experiments. The Boson peak is typically ascribed to an excess density of vibrational states. Shintani and Tanaka [45] studied the nature of the boson peak, using numerical simulations of several glass-forming systems. They have discovered evidence suggestive of the equality of the Boson peak frequency to the Ioffe-Regel limit for “transverse” phonons, above which transverse phonons no longer propagate. Their results indicate a possibility that the origin of the Boson peak is transverse vibrational modes associated with defective soft structures in the disordered state. Furthermore, they suggest a possible link between slow structural relaxation and fast Boson peak dynamics in glass-forming systems.

Figure 4: Au_N (N=14): α_i=ω_i/(0.6950356*T) of eqn. (8) and the corresponding Boson peak C_vib=T³ vs T.

However, Malinovsky and Sokolov [46] found that the form of a low-frequency Boson peak in Raman scattering is universal for glasses of varying chemical composition. They have shown that from the shape of the Boson peak one can determine the structural correlation function, i.e., the character of violations of ordered arrangement of atoms within several coordination spheres in noncrystalline solids. Most importantly, very recently Milkus and Zaccone found [47] that bond-orientational order is not so important for the boson peak. Whereas a much more important parameter is the local breaking of inversion symmetry. Indeed, there is similar behavior of heat capacity in glasses and clusters at low temperatures. Glasses have some distribution of interatomic distances and modification of atomic coordination induced by disorder, compared to periodic crystals [48]. In clusters or nanoparticles, it is caused by the reduced atomic coordination of the surface atoms. Because the ratio of surface to volume is large, the number of atoms with reduced coordination is significant. The vibrations of surface atoms enhance the VDOS at low energies and the heat capacity increases. The Boson peak is usually studied in glasses, where enhancement of heat capacity is induced by disorder. The modeling of clusters may be important for understanding the mechanism which lead to this effect. In glasses, there are different local configurations of atoms that may be simulated by isolated clusters. In particular, it was found that the vibrational density of states (VDOS) exhibit an excessively low-frequency contribution. A corresponding low-temperature peak is observed in the temperature dependence of the specific heat if plotted as C_vib(T)=T3. A plot of the low-T heat capacity normalized to T-cubed (Figure 4) reveals in detail the deviations from the Debye T3 law [49,50]. Based on the experimental observations, the maximum in silica glass is placed at about 10 K and 8.5 K for neutral gold cluster (see Figure 4, and Richet et al. [49,50]), and the maximum deviation C_vib/T³ attains 2.4 × 10^-4 J=(molK) for silica glass, and 0.0004 kB=atom for gold cluster, respectively. Please notice that the units are not the same.

We investigated the heat capacity at a low temperature range (0.5-300/950 K) of the re-optimized global optimum gold cluster as a function of their size Au_N=14. Our first step towards the understanding of the so-called finite temperature effects was to take into account the vibrations of clusters. We focused our interest on the cluster size and temperature dependence of the heat capacities and the free energies of the clusters. Finally, we have studied vibrational and thermodynamic properties of the clusters in order to explore the interaction between stability, structure, and heat capacities of clusters. Our approach is worthy of further investigation and would pave a way in realizing numerical values which would allow for an experimental vibrational spectrum and heat capacity, which would prove crucial in development of nanoelectronic devices. Nevertheless, our work gives a possible cause for the size, temperature, and structures effect of Au atomic clusters. This novel and reliable methodology is constructed to explain the essence of the physical picture.

This work was supported by the German Research Council (DFG) through project Sp 439/23-1. We gratefully acknowledge their very generous support.