θ_m: preferential angle associated with the whole numbers l and m

l and m :whole numbers such as m>0 and l ≥ m

β: apex angle

Co: height of wing

h: height of cone

R: radius of the circular base of the cone

i: incidence

Vo: speed of the flow at infinite up stream

Re: Reynolds number

α₁: the main or interior inter vortex angle for wings

α₂: the secondary or exterior intervortex angle for wings

ω₁: the main or intervortex angle for ogives or cones

ω₂: the secondary or exterior intervortex angle for ogives or cones

Quite a considerable number of studies have been carried out to date into delta wings, ogival wings, cones and also into more or less simple slender bodies formed from combinations of such components; the findings have dealt as much with the development of approximate theories as with the definition of models specifying vortex lift by unit area.

Visualisations of hyper lifting vortex structures, mainly those carried out by Werle H [1-6], the analysis of pressure and speed fields created by these vortices, with or without breakdown - notably the analysis by Solignac et al. [7] also provide quite outstanding studies that are the standard works in their fields.

Already described fully in such papers as, for example, those by [8-11] and Stahl [12], these findings offer today entirety a thorough knowledge of the properties of various types of slender bodies.

However, given that the character of most of the aspects referred to remains empirical and limited to this or that degree of incidence [1-4] or to a numeric range [5], the way lies open, starting out from experimental data and various factors of analysis [6], for new attempts to be undertaken to examine the fundamental problems related to the position of vortices created by such slender bodies.

A large number of photographic visualisations, concerning vortex flows developed on the upper surface of delta or ogival wings and cones, have been carried out at the Valenciennes University (France) laboratory [7] in such a way as to provide a better understanding of the development and positioning of vortex structures at not only low and mean incidence but also at high incidence.

These visualisations have enabled priority to be accorded to the study of examples of the most elementary shaped section, i.e., delta and ogival wings.

The results obtained in these two cases, fully described in previous articles and papers [6,8], may be acknowledged to have remarkable simplicity and consequently convey the fundamental nature of these studies.

The intervortex angles have been found, under experimental conditions, to have a preferential nature thereby underlining a simple angular characterisation of the relative positions of single or double vortex torques.

Geometrical description

The profile under investigation in the wind tunnel is a double-delta wing having an apex angle β=29° and a chord Co=240 mm. It is 1 mm thick (Figure 1).

Figure 1: Geometrical description of double-delta wing.

Analysis of the results

The evolution of the vortex phenomena was traced in terms of that parameter which exerts the greatest influence on them, namely the angle of incidence of the configuration in relation to the flow. The visualisations were carried out at an upstream speed of flow of 3 m/s.

A reminder of the main phenomena taking place at low and mean incidences

• i=0°: the flow is uniform on the upper side of the wing. The boundary layer is observed but there is no flow separation as yet.

• i=2°, i=5°: the upstream flow skirts around the leading edges of the profile. Three zones become organised into a central zone and two external ones. The hyper lifting vortices resulting from the separation of the boundary layer begin to appear as increasingly organised structures.

• i=8°: the main and secondary vortices are clearly detected and have now become individualised, concentrated and separated from boundary layer. The central zone is visualized and fading out.

• i=10°, i=15°, i=20°: the vortices increase in strength. Both the vortex flow and the direction of the rotation of the vortices are clearly seen. Then central zone has disappeared. The presence of tertiary vortices is to be noted although they are extremely difficult to visualise. There is no breakdown as yet.

• i=25°: the breakdown phenomenon makes its appearance. The main vortices are breaking down a long way downstream from the profile: in fact, a more diffused mass of smoke is observed in this zone. The secondary vortices have broken down upstream from the trailing edge; as for the tertiary ones, which are difficult to observe because of their positioning at the edge of the boundary layer, it seems that they break down in the area close to the apex and coil around the main and secondary vortices. Once the secondary vortices have broken down, they also coil around the main ones. The asymmetry of the breakdown point of the main and secondary vortices is to be noted.

• i=30°: the tertiary vortices have now completely disappeared. The secondary ones are breaking down in the area of the trailing edge of the profile.

• i=40°: the secondary vortices break down near the apex whereas the point of breakdown of the main ones has advanced to a third of the way along the chord. A sudden expansion at the core of the main vortices is still discernible, followed by an unstable zone showing quite considerable turbulence.

Not that the position of the breakdown point is estimated on the basis of a main reading of the respective breakdown points of the righthand and left-hand main vortices.

• i=45°: the main vortices break down at the fore quarter of the chord; the secondary ones are absorbed by the main vortices at the apex and no longer visible.

• i=50°: a total breakdown of the vortices takes place at the apex. Intense turbulence is observed at about the trailing edge (Figures 2-4).

Figure 2: Vortex structures developed on the upper surface of double-delta wings.

Figure 3: Profile view of vortex structure.

Figure 4: View of vortex structure.

Interpretation

Comments: the breakdown of the secondary vortices is not as impressive as that of the main ones. In fact, the vortex cores of the latter, after having maintained a cone-shaped form increasing in diameter towards the downstream side, undergo a sudden expansion into a brush-shaped form (the rate of expansion is approximately three to four times the diameter of the vortex core upstream from the point of breakdown). The point of breakdown is immediately followed by a zone in which the flow circulates again and the by an area of intense turbulence. The thin streams of smoke indicating the main vortices seem to change direction at the point of breakdown and to follow a spiral trajectory downstream.

• The pulsation phenomenon of the vortex breakdown has become highly conspicuous from now on the breakdown points undergo quirt considerable positional fluctuations. The broken down vortices seem “to dance”.

• On placing an object in the axis of the broken down vortices, it can be seen that the breakdown points “rise again” in an upstream direction but it is also noticed that the breakdown point of the secondary vortices is still located upstream from that of main vortices.

The presence of preferential intervortex angles is observed.

Intervortex angles on the wings:

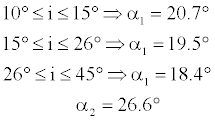
The experiment has shown: first, a layer on the upper surface of the wing as regards low incidences and the start of the formation of vortex structures with steadily flowing thin streams becoming separated from each other and heading towards the leading edges. Furthermore, the formation of two vortices since all wings under investigation has a non-preferential apex angle. Moreover, for i>45° the two vortices overlap each other. Therefore, this leads to the appearance of the torch phenomenon (spiralling effect) constituting the disappearance of the intervortex zone.

The exterior secondary system is less significant than and not as dense as the main system and is the first one to deteriorate.

The law of filiations is examined between the two systems: the angle of the secondary system begets that of the main system.

The breakdown evolves in relation to the incidence. It is a function of the apex angle: the greater the apex angle, the sooner the breakdown takes place (Figures 5 and 6).

Figure 5: Vortex structure in upper surface of wing view for β=45°, i=30°, α₁=30°.

Figure 6: Vortex structure in upper surface of wing view for β=74.5°, i=30°, α₁=45°, α₂=63.4°.

As regards moderated angles of incidence, the vortex structures of the aerofoil wing and of the canard surface remain separated.

When the angle of attack increases, the vortices coming from the canard plan evolve closer to the surface of the rear section of the aerofoil wing and towards its exterior.

As regard high incidence, the merging process of the two vortex structures begins at about the aerofoil wing: this leads to the fact that no more than one sole vortex structure exists on the surface of the aerofoil wing being the result of the joining of the other two structures.

Those vortex flows which are developed on such double-delta or delta-canard-wing-body configurations are quite complex : vortex flows can, of course, be observed on the leading edges of the airfoil wing, but they also appear on the leading edges of the canard-wing. These two vortex structures interact with one another [9].

Giving prominence to the preferential nature of those intervortex angles present on the upper surface of cones constitutes, moreover, a generalisation-as regards the basic three-dimensional cone-formed from observations previously made at valenciennes on delta and ogival wings; it has thereby been revealed that vortex behaviour has something of a universal nature.

At the present time, no complete theoretical approach seems to be sufficiently adequate to provide a straightforward explanation of the remarkable simplicity of these findings [10].

In other respects, it would appear interesting to recall that those particular spatial organisations of vortex structures citing the concept of preferential angles also appear in stand and theories on hydrodynamics and aerodynamics as in, for example, those governing aerodynamic drag. In such slipstreams, the crests of the waves, in the form of curvilinear triangles, will in fact each disappear at two counter-flow points, the alignment of which, along two right-hand sides constituting the raised edges of the slipstream, reveals a double angle of 19.4° in relation to the axis of the same slipstream [11-28].

A large number of questions remain to be investigated; further research can be undertaken in particular into the link between interior and exterior vortex structures. In addition, the least resistance of secondary vortices in relation to the breakdown inevitably calls for experimenting with other possible elementary combinations of slender bodies that would enable the appearance of the breakdown to be delayed. Somme studies would even show the existence of a supplementary vortex torque.