Journal of Oceanography and Marine Research
Open Access
ISSN: 2572-3103
ISSN: 2572-3103
Research Article - (2017) Volume 5, Issue 4
In this investigation, the execution of the wave model WAM Cycle 4.5.3 was evaluated; based on the forcings by two distinct wind fields namely ERA-40 and QuikSCAT-NCEP Blended winds in the North Indian Ocean. Using the past analysed winds (hindcasting) and with boundary conditions generated from 1° x 1° global runs the wave model have been implemented for the North Indian Ocean from 50°E to 100°E and 0°N to 30°N. The model simulated parameters namely significant wave height (Hs), mean wave periods (Tc), mean wave direction, swell wave height (Hsw), swell wave period (Tsw) and swell wave directions are presented. Further, the predicted waves are compared against in-situ wave measurements. The simulated wave parameters obtained as outputs from numerical simulations such as Hs and Tc; collocated in space and time have been compared with buoy measurements in the Arabian Sea and Bay of Bengal with the aid of statistical error indicators. Comparison between the predicted and observed wave parameters are very encouraging, excepting the higher model estimates of significant wave height and the disagreement in lower wave heights at few buoy locations. Further, the sensitivity of the model to two different wind fields was analyzed and it is noted that the blended winds could accurately reproduce Hs and Tc at the buoy locations. The present study suggests that, WAM Cycle 4.5.3 model predictions are quite reliable for the Indian seas using the analysed wind fields such as ERA-40 and QuikSCAT/NCEP Blended wind fields. However, the performance of wave model was best when blended winds were used. Despite several limitations, the results reveal that the performance of third generation wave model is promising and the correlation and deviation of simulated and measured waves are critically inspected.
<Keywords: ERA-40; QUIKSCAT/NCEP blended; WAM; Wave model validation; Buoy; Wave hindcast
Ocean wave hindcast and forecast are of preeminent concern for the management of coastal and offshore structures/constructions, ship navigation and various naval operations. The in-situ observations are location-specific and generally sparse. Sverdrup and Munk [1] were the first to develop operational wave prediction technique. The technique was purely statistical and was based on just one parameter, viz., the significant wave height. In other words, the spectral character of the sea state was completely neglected. Later, the spectral characteristics of waves were taken into account for the development of methods based on wave spectrum. The wind-wave interactions have been studied with the aim of wave hindcasting, nowcasting and forecasting. At present, there are numerous spectral wave models for wave hindcast and forecast studies in the open ocean as well as in the coastal/near-shore zone. The state-of-the-art third generation wave models developed are WAM (WAMDI, 1988), WAVEWATCH III [2], and SWAN [3].
Performance evaluation studies of the third generation wave model WAM were achieved (both in operational forecast as well as hindcast modes) by various authors and the results have been documented. It is stated that, even though, the third-generation wave models are capable of simulating waves accurately, they can in any case be enhanced with a suitable demonstration of greatly complex physical processes of wind induced waves [4-6]. There has been considerable advancement in the field of wave modelling and prediction all over the world [7- 12]. In the past a number of studies are carried in the North Indian Ocean using deep water wave models WAM and WAVEWATCH III [13-16]. In India, with the launch of OCEANSAT-I (IRS-P4) in 1999, extensive validations were performed with the third generation wave model WAM C4 for the Indian Ocean region using the analysed wind fields provided by NCMRWF [17]. Later in 2009, when OCEANSAT II was launched, researchers have taken considerable interest in using Scatterometer winds as inputs for wave models [18]. Few other studies revealed that, the WAM simulated model outputs are very useful for navigation and ship routing [19,20].
The principal objective of this investigation was to carry out hindcast experiments using ERA-40 and QuikSCAT/NCEP blended wind fields by implementing the latest version of WAM model (WAM Cycle 4.5.3) for the North Indian Ocean and to validate the predicted wave parameters with available in-situ measurements. The study utilized the output of the global model at the boundary and carried out the simulations in the North Indian Ocean. Further, the sensitivity of the model to different wind forcings was investigated to assess the performance of the model using statistical error analysis.
WAM Cycle-4.5.3 used in the present study [21] is an updated version of WAM C4.5 wave model. WAM C4.5.3 assimilates the source function integration scheme suggested by Hersbach and Janssen [21] and Bidlot et al. [22] which is a new semi-implicit approach advanced at ECMWF as shown below:
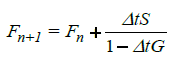 (1)
(1)
Where S=S(un+1, Fn) represents the source function of spectrum computed at time (n) and wind speed (u) at time level (n+1). The term ‘G’ in the above equation is given by G=G(un+1, Fn). The other developments in this version attributes to the dissipation source function indicated in terms of mean steepness and specification of mean frequency giving more importance to the high frequency part of the wave spectrum. These new additions in version 4.5.3 provide a more realistic interaction between wind-sea and swell waves, which in turn allows the relaxation of the prognostic frequency range over which the model equations are integrated. Further, a few other small adjustments were also necessary to take advantage of the increased dynamic range of the model [22]. Another improvement is with reference to the time-stepping algorithm, which allows propagation time step to be longer than source function time step. All these led to the advantages in computational speed, which is boosted for very high spatial resolutions. In addition to the above, in WAM C4.5.3 the windgeneration function and dissipation terms implement the Janssen’s formulation, and the nonlinear interaction source function is evaluated using the Discrete Interaction Approximation (DIA) [23,24]. More details of WAM C4.5.3 may be seen from Gunther and Behrens [21].
The wave model outputs are critically dependent upon the quality of input fields. Hence, the study has taken utmost care in using best quality products such as ERA-40 and QuikSCAT-NCEP Blended wind fields as inputs for the wave model. ECMWF 40 Year Reanalysis (ERA- 40) is a reanalysis of meteorological observations from September 1957 to August 2002 (45 years), released by ECMWF [25]. ERA-40 consists of 6-hourly global fields of wind speed at 10 metres height (U10) with a 1.5º x 1.5º grid resolution [26]. In this study, the wind speed and the stresses (τx and τy) for the year 2000 was extracted from ERA-40 and the same was used to estimate wind direction; and the winds were further interpolated to 1º x 1º grid resolution. The processed six hourly winds for January, April, July and October 2000 were then used to force the wave models WAM for the global and North Indian Ocean. The QuikSCAT/NCEP blended wind products were derived through a spatial blending of the high-resolution scatterometer (QuikSCAT) wind observations with the NCEP/NCAR reanalysis winds [27,28]. These data files are available from the NCAR Data Support Section (DSS): DS744.4 - QSCAT/NCEP Blended Ocean Winds. QuikSCAT/NCEP blended winds (six-hourly) for July 2008 and January 2009 have been downloaded and interpolated to 1º × 1º (model grid resolution) for the purpose of wave hindcasting. Ocean Surface Currents Analyses Real time (OSCAR) used as model input in this investigation is obtained [29] from the NOAA site (www.oscar.noaa.gov) on a 1º global grid.
Since 1997 [30] the National Institute of Ocean Technology, Chennai under the National Data Buoy Program (NDBP) has deployed several deep-sea and shallow water moored buoys (in-situ measurements) to measure several near surface meteorological and oceanic variables in the Indian Ocean region, The comparison of hindcast wave parameters have been executed using this data [30] of nine selected buoys of NIOT, Ministry of Earth Sciences, Govt. of India as shown is Figure 1. The buoy data have proved to be extremely useful in validating re-analysis and satellite products [31-34]. These buoys are functional at a water depth from 20m to full ocean depth, excepting few buoys, which are also operable at slightly lower depths. The sensor used in the measurement of wave parameters is an inertial altitude heading reference system with dynamic linear motion measurement capability.
The waves are measured in the buoy by a motion reference unit, which measures absolute roll, pitch, yaw and relative heave. These data are recorded at a rate of 1 Hz for 17 min every three hours. It measures the full spectrum of the waves for 17 min. The Hs is estimated as four times the square root of the area under the non-directional wave spectrum. It has an accuracy ± 10 cm for wave height up to 20 m and ± 5° for wave direction. The significant wave parameters such Hs and Tc from the selected buoys in the North Indian Ocean is utilised in this study.
In this study, wave data measured at deepwater locations such as DS1 (off Goa) during January, April, July and October 2000, DS2 (off Lakshadweep) during January, April, July and October 2000, DS3 (off Andaman & Nicobar) during July and October 2000, DS4 during October 2000, OB10 (off Chidambaram) during January 2009 and SW1 at shallow water locations off Pipavav port during January, April, July and October 2000, SW4 (off Mangalore port) during January, April, July and October 2000, SW5 (off Tuticorin port) during January, April, July and October 2000 and SW6 (off Chennai port) during April, July and October 2000 are utilized for the validation of wave model (WAM) hindcasts. The locations of these buoys are shown in (Figure 1).
WAM C4.5.3 has been implemented [21] for wave prediction (hindcasting or simulation) using analysed winds for the full globe as well as the regional grid system (North Indian Ocean or Indian Seas). The global grid system of the wave model covers the geographical extent, 0° to 360°E and 77°S to 77°N with a resolution of 1° × 1°. The bathymetric map has been constructed from ETOPO2 data. The model uses 25 frequencies ranging from 0.04177 Hz to 0.41145 Hz and 12 directions (constant increment) to represent the 2d-wave spectral distribution. The wave model was executed for the completely global grid, whereas the boundary outputs have been utilized for the regional domains (0° to 30°N; 50°E to 100°E). Source integration and propagation time steps were set to 10 minutes and 20 minutes for the global run and; 5 minutes and 15 minutes respectively for the regional model run. The wave model was driven with six-hourly ERA-40 and QuikSCAT/NCEP Blended winds; and OSCAR surface currents with similar resolutions of 1° x 1° longitude-latitude grids. The WAM C 4.5.3 model outputs for various wave parameters were stored every 6-hourly. Two case studies have been carried out for analysed winds (Case-I: January, April, July and October 2000) using ERA-40 winds and another (Case-II: July 2008 and January 2009) using QuikSCAT/NCEP Blended winds. The months of January, April, July and October 2000 were chosen with the consideration that January and July are the peaks of northeast and southwest monsoon respectively; and April and October are the premonsoon and post-monsoon months/periods respectively.
Case-I: January, April, July and October 2000
In this investigation (Case-I) - ERA-40 analyzed winds have been utilized as input to force the WAM model for the four chosen months namely January, April, July and October 2000. The spatial distribution of sample input wind fields for the North Indian Ocean for a selected day (25th, 1200 hrs of each month) is presented in (Figure 2) followed by a brief analysis of prevailing wind and the hindcast waves.
(Figure 2) shows the wind speed and direction at 1200 h of 25 January, 25 April, 25 July and 25 October 2000 respectively. Reasonably strong winds ranging 4 to 9 m/s with direction around northeast prevailed on 25 January, being the fair weather season. Higher winds around 9 m/s were seen in south central Bay. During April, the winds are generally low and variable. However, relatively higher winds were seen (around 7-9 m/s) in southwestern Bay and northern extreme of Arabian Sea on 25 April 2000, 1200 hrs, which is likely to be the premonsoon activity. It may be specifically noted from the (Figure 2c) that the normal southwest monsoon winds were active all over the North Indian Ocean with speed ranging from 6-10 m/s, and the noticeable stronger jet is noticed off the Somalia coast. A weak low pressure system was noticed in the central Bay with moderate westerly winds (6-8 m/s) around southeast Arabian Sea and southern parts of Bay of Bengal (Figure 2d).
The spatial distributions (contour plots) of Hs, Tc, Hsw and (Tsw) at 1200 hrs of 25 January, 25 April, 25 July and 25 October 2000 are presented in (Figures 3-5) respectively. The Hs varied from 1 to 2.2 m (25 January 2000, 1200 hrs) with a gradual increase from north to south of North Indian Ocean (Figure 3). The mean wave direction follows the climatic pattern. The Tc, Hsw and Tsw as shown in (Figure 3) show spatial variations of 6 to 10s, 1.0 to 1.8 m and 8 to 11s respectively. The spatial distribution of Hs, mean wave direction, Tc, Hsw and Tsw for 25 April 2000, 1200 hrs are plotted in (Figure 4). Hs varied from about 1.4 to 2.2 m in the Arabian Sea and 0.6 to 1.8 m in the Bay of Bengal. Tc varied between 8 and 12s in the Arabian Sea, whereas it varied from 8 to 11s in the Bay of Bengal. The mean wave directions more or less agree with the wind pattern over the Arabian Sea but northwesterly in the Bay of Bengal while the wind direction vary from southerly to southwesterly. Hsw ranged between 1.2 and 2 m in the Arabian Sea, whereas it varied 0.6 to 1.8 m in the Bay of Bengal. Tsw varied from 10 to 12s in the Arabian Sea and 8 to 11s in the Bay of Bengal respectively.
The southwest monsoon is considered as the rough weather season [35] from wave climate point of view during which the wind and wave conditions in the Arabian Sea and Bay of Bengal (Indian Seas) are considered to be high [36]. However, the wave periods and swell parameters are normally not related to the local winds as the wave propagate from different areas after their generation, which is evident from the model outputs (July 2000). In the Arabian Sea (Figure 5), Hs varied from 1.2 to 2.6 m with Tc ranging from 8 to 12s. Hsw varied from 1.2 to 2.2 m with Tc 10 to 12s. However, in the Bay of Bengal, Hs was lower (0.8 to 1.6 m) as compared to the Arabian Sea. Tc varied from 6 to 10s, Hsw from 0.8 to 1.4 m and Tsw from 8 to 10s.
Apart from above, an attempt has been made based on the simulated wave spectra to arrive at its specific characteristics. In this hindcast case study of July 2000 alone, three sample wave spectra for a selected location (LOC1: 12°S, 67°E, Southern Arabian Sea as shown in (Figure 6a) and the time-series of few selected wind and wave parameters (LOC2: 15°N, 90°E, Bay of Bengal as shown in (Figure 6a) have been shown in (Figures 6 and 7) respectively.
The sample plots of 1D (frequency) spectra for 10 July (1200 hrs) and 20 July 2000 (1200 hrs) and the mean spectra (LOC1: 12°S, 67°E) for the month of July 2000 as shown in (Figure 6) reveal multi-peaked spectral characteristics indicating the presence of both wind seas and swell waves. Although the winds during July (southwest monsoon) are strong and steady, the major wave generating areas can be more than one including the swells which propagate from the southern hemisphere. The frequency spectrum of 10 July 2000, 1200 hrs belong to the active monsoon phase with a minor swell component, sometimes the locally generated swells. However, the spectrum of 20 July 2000, 1200 hrs and the six-hourly averaged mean monthly frequency spectrum for 01-31 July 2000 from the location in the southern Arabian Sea depicts similar features (spectra with two peaks) with well-defined swell peaks and secondary wind sea peaks.
The time-series of wind and hindcast wave parameters at the selected location (LOC2: 15°N, 90°E, 01-31 July 2000) as shown in (Figure 7) indicate moderate wind and wave variability with wind speed ranging between 4 to 12 m/s and Hs between 0.5 to 3.0 m. The locally generated wind seas dominated over swell waves only for a few days of the month (5 to 8 days) during which the prevailing winds at the site were relatively higher. The associated mean and peak wave periods for the combined wind sea and swell (Figure 7), wind seas and swells reveal a consistently changing sea state composition involving variable energy levels for the wind seas and swell waves. While the direction of the combined sea state varied from south to southwesterly, the wind seas and swell waves show directional variability ranging from 30 to 60 degrees. However, the predominant wave direction was southwesterly.
The hindcast wave parameters for 25 October 2000, 1200 hrs as shown in (Figure 8) is an indication of lower wave activity with minor spatial variability, Hs being higher in southeastern extreme of North Indian Ocean. The Hs varied from 1.4 to 1.8 m in the Arabian Sea, while in the Bay of Bengal it ranged from 1.0 to 2.2 m. The Tc varied from 11 to 12s in the Arabian Sea and from 8 to 13s in the Bay of Bengal indicating a larger variability. The hindcast Hsw ranged from 1.4 to 1.8 m in the Arabian Sea while it varied from 1.0 to 1.8 m in the Bay of Bengal. In the Arabian Sea, Ts varied from 11 to 12s, and in the Bay of Bengal it ranged from 9 to 13s.
In this case study involving four months of wave hindcasts using ERA-40 winds is infact, a consolidation of typical examples mimicking the general pattern of wind and wave variability in the North Indian Ocean during pre-monsoon, south-west monsoon, north-east monsoon and post-monsoon periods in the North Indian Ocean. The model outputs and their ranges of variabilities in space and time for the four selected months (year 2000) are adequate and useful for the validations using the in-situ measurements that will be discussed in the succeeding section dealing with wave model validations.
Case-II: July 2008 and January 2009
Case-II used the QuikSCAT/NCEP blended winds as input to force the WAM Model. The spatial distribution of input wind fields for the North Indian Ocean for the selected day (25th, 1200 hrs) are presented for the months of July 2008 and January 2009 respectively in (Figure 9). Figure 9a shows the wind speed and direction for the 25 July 2008, 1200 hrs, which is predominantly southwesterly. However, the winds turned westerly near the coast and turned further around northwesterly very close to the coast while approaching the landmass (Western Ghats). This is a consistent and regular feature of southwest winds, which may vary marginally from north to south along the west coast of India. (Figure 9a) clearly depicts the very high wind speeds, which prevail during July, being the peak of southwest monsoon. Compared with July 2008, the wind speeds were low for 25 January 2009, 1200 hrs (Figure 9b) being the fair weather period. However, as indicated before, January is the peak of northeast monsoon. On 25 January 2009 (1200 hrs), the winds were low to moderate which ranged from 2 to 8 m/s; and wind directions were predominantly northeasterly. The spatial distributions or the contour plots of hindcast Hs, mean wave direction, Tc, Hsw and Tsw for 25 July 2008, 1200 hrs and 25 January 2009, 1200 h are presented in (Figures 10 and 11) respectively.
The spatial variability of wave parameters shown for 25 July 2008, 1200 hrs, is a typical example of high wave activity during the peak southwest monsoon period during which Hs reaches around 5 to 6 m off the Somali coast and 3 m waves are noticed in the Bay as per the wave climatology of the region. In this case, as shown in (Figure 10), the Hs varied from 2.0 to 5.0 m in the Arabian Sea, while in the Bay of Bengal it ranged from 1.5 to 3.0 m. The Tc varied from 8 to 12s in the Arabian Sea and from 8 to 11s in the Bay of Bengal, which is consistent with the corresponding Hs fields. Similarly, the hindcast Hsw varied from 1.5 to 3.0 m in the Arabian Sea, and in Bay of Bengal it varied from 1.0 to 2.5 m. In the Arabian Sea, Tsw varied from 11 to 13s, while in the Bay of Bengal it ranged from 10 to 12s.
In the above mentioned case study (Case-II) using QuikSCAT/ NCEP blended winds, simulations were also carried out for the month of January 2009. The hindcast Hs varied from about 1.5 to 2.4 m in the Arabian Sea and 1.1 to 1.8 m in the Bay of Bengal (Figure 11). Tc varied between 8 and 12s in the Bay of Bengal, whereas it varied from 10 to 11s in the Arabian Sea. The hindcast Hsw varied from 1.6 to 2.2 m in the Arabian Sea and 1.0 to 1.8 m in the Bay of Bengal. Tsw was around 11s in the Arabian Sea, while it varied from 6 to 12s in the Bay of Bengal. This is yet another example of wind and wave variability during January (peak of northeast monsoon) 2009, during which the mean wave directions as well as the swell directions were around north (± 150). This is a typical case which normally depend on the prevailing wind conditions during the period of study, whereas the wave direction during January vary from northeasterly to northwesterly form climatological point of view, considering the whole of North Indian Ocean.
Wave model validations
Validation of a preferred model for a specific geographic location against observation is an important and essential step involved for improved wave prediction and analysis for the region of interest. Based on the availability of buoy data pertaining to the study period and the region of interest, comparisons have been made between buoy and model derived wave heights and wave periods. To undertake the intended job of wave model validations and to evaluate further the model performance, the hindcast Hs and Tc which have been chosen have been compared with the observations. The results of wave model validations are discussed in the following sections.
The in-situ met-ocean parameters such as Hs and Tc of NDBP being executed by NIOT for the buoys named DS1, DS2, SW1, SW4, DS3, DS4, SW5, SW6 and OB10 have been co-located with WAM model outputs available at the centre of the grids considered and interpolated in space and time for the comparisons. A detailed statistical error analysis was performed for each dataset to evaluate the model performance. Various statistical measures such as Coefficient of Correlation (R), Scatter Index (SI), Bias (B, mean error), Root Mean Square Error (RMSE), Percentage Error (PE) and Model Performance Index (MPI) between measurements and model computed parameters are examined extensively to evaluate the model hindcasts as practiced by many investigators in the earlier studies [8,37-43].
(Figures 12-15) show the comparisons between the observed and predicted wave parameters (Hs and Tc) at 6 hourly intervals for the period 01-31 January 01-30 April, 01-31 July and 01-31 October 2000 respectively. In (Figure 12), the WAM model outputs (continuous line in blue) are compared with measurements from five buoy (solid dots in red color) locations such as DS1, DS2, SW1, SW4 and SW5. The length of the time-series or the number of data points plotted for comparison between the model and buoy observations may vary due to missing buoy data as shown in the different plots.
In general, the model predicted parameters Hs and Tc as shown in (Figure 12) reveal reasonably good correlation with the observations in most cases, although there exists notable over prediction by WAM. The statistics of the comparison of WAM model wave parameters with buoy measurements in the Indian Seas during January 2000 is shown in (Table 1). The buoys DS1, DS2, SW1 and SW4 in the Arabian Sea versus the model hindcasts for Hs, indicate correlation coefficients of the order 0.86 to 0.94, while in the Bay of Bengal, it is 0.96 for SW5. Similar case studies were also carried out by Magnar et al. [44] in the northeast Atlantic Ocean in which buoy Hs were compared with WAM Hs, which revealed a strong correlation of 0.95. Here in this study, the estimated mean values and ranges for the buoy measurements and the model hindcasts for Hs are well comparable (deviations within 0.1 to 0.2 m), excepting at the buoy location SW1; where although the measured range varied from 0.1 to 0.9 m, most observations were around 0.2 m while the WAM prediction ranged between 0.4 and 1.1 m. In some cases, it has been difficult to achieve such reliabilities during low wind and wave activity periods. The low values of SI for the buoys DS1, DS2, SW1, SW4 and SW5 respectively indicate a better fit between the model and measurements. Hs shows negative bias at all the locations considered (DS1, DS2, SW1, SW4 and SW5) indicating overestimation by the wave model WAM. The RMSE is low in all cases, which reveal a better agreement between the model and the buoy observations. The PE for Hs is lesser than 22% in most cases except only one case (SW1) where it is higher (41.6%), which may be due to the prevailing low wave activity. Higher values of MPI for the buoys DS1, DS2, SW1, SW4 and SW5 reveal better performance (WAM) with the use of buoy measurements for validation. During the month of January 2000, it is noted that the lower wave heights are not estimated properly by WAM using ERA-40 winds. This may be attributed to simplifications like the neglect of atmospheric stratification effects when converting wind speeds to the wind stress fields driving WAM.
| 1.1. Significant wave height (Hs in m) | ||||||
|---|---|---|---|---|---|---|
| Sl. No | Statistical estimates | Arabian Sea | Bay of Bengal | |||
| DS1 | DS2 | SW1 | SW4 | SW5 | ||
| 1. | Mean (Buoy) | 1.1 | 0.8 | 0.3 | 0.6 | 0.9 |
| 2. | Range (Buoy) | 0.5 – 1.7 | 0.6 – 1.2 | 0.1 – 0.9 | 0.3 – 1.2 | 0.5 – 1.7 |
| 3. | Mean (WAM) | 1.2 | 1.0 | 0.5 | 0.8 | 1.0 |
| 4. | Range(WAM) | 0.7 – 1.8 | 0.6 – 1.3 | 0.4 – 1.1 | 0.4 – 1.3 | 0.6 – 1.6 |
| 5. | R | 0.94 | 0.86 | 0.89 | 0.94 | 0.96 |
| 6. | SI | 0.03 | 0.05 | 0.16 | 0.05 | 0.01 |
| 7. | B | -0.14 | -0.18 | -0.22 | -0.17 | -0.08 |
| 8. | RMSE | 0.03 | 0.04 | 0.05 | 0.03 | 0.01 |
| 9. | PE | 12.7 | 18.7 | 41.6 | 22.1 | 10.8 |
| 10. | MPI | 0.97 | 0.95 | 0.87 | 0.94 | 0.98 |
| 1.2. Mean wave period (Tc in s) | ||||||
| 1. | Mean (Buoy) | 4.5 | 5.1 | 4.4 | 4.2 | 3.7 |
| 2. | Range (Buoy) | 3.6 – 6.2 | 4.2 – 6.9 | 2.6 – 9.5 | 3.0 – 5.9 | 3.1 – 4.4 |
| 3. | Mean (WAM) | 5.1 | 6.0 | 5.1 | 5.2 | 4.6 |
| 4. | Range (WAM) | 4.3 – 6.7 | 5.0 – 7.4 | 3.6 – 8.7 | 3.7 – 6.8 | 3.6 – 5.7 |
| 5. | R | 0.68 | 0.70 | 0.96 | 0.86 | 0.62 |
| 6. | SI | 0.13 | 0.18 | 0.15 | 0.26 | 0.29 |
| 7. | B | -0.66 | -0.89 | -0.63 | -0.99 | -0.95 |
| 8. | RMSE | 0.57 | 0.94 | 0.68 | 1.08 | 1.09 |
| 9. | PE | 12.8 | 14.9 | 15.5 | 19.3 | 19.7 |
| 10. | MPI | 0.87 | 0.85 | 0.86 | 0.78 | 0.76 |
R: Correlation Coefficient, SI: Scatter Index, B: Bias, RMSE: Root Mean Square Error,
PE: Percentage Error & MPI: Model Performance Index.
Table 1: Statistics of the comparison of WAM model wave parameters with NIOT buoy measurements in the Arabian Sea and Bay of Bengal during January 2000 using ERA-40 winds as shown in figure 12.
Considering all the buoys (DS1, DS2, SW1, SW4, and SW5), the value of Tc as shown in (Figure 12) varied from 3.7 to 5.1s, whereas it varied from 4.6 to 6.0 based on WAM hindcasts. It reveals that the WAM predicted Tc is about 0.6s to 1.0s higher than the measurements. However, the predicted Tc and the measurements show correlation coefficients in the range 0.68 to 0.96 for buoys in the Arabian Sea, which are in agreement with the earlier results by Magnar et al. [44]. Here, Tc was well represented in the comparisons between buoy and WAM with correlation coefficient of 0.92. The correlation coefficient is relatively low (R=0.62) for SW5, in the Bay of Bengal. Values of SI are seen to be lower which indicate a better comparison between the observed and hindcast Tc. The values of B are negative throughout indicating relatively higher values of Tc as predicted by WAM. The PE for all buoy locations remained within 20%, although it was a fair weather season (January 2000).
From the above discussion (Figure 12) on the statistical estimates and the analysis of wind and wave variability as explained before, it may be concluded that, the WAM model derived wave parameters such as Hs and Tc compared well with the observed wave parameters in most cases for January 2000. However, the hindcast Hs and Tc are overestimated up to the maximum extents of 0.2 m (Hs range 0.1 to 1.7 m) and 1.0s (Tc range 2.6 to 6.9) respectively. The PE remained within 20% in most of the cases. Although, the hindcast Hs and Tc showed a negative bias throughout the simulation period, the MPI values revealed satisfactory performance of WAM for January 2000 for most of the buoys.
(Figure 13) shows the comparison between the observed and predicted wave parameters (Hs and Tc) of WAM for the period 01- 30 April 2000. Here, the model outputs are validated for six buoy locations such as DS1, DS2, SW1, SW4, SW5 and SW6. Compared with the previous case of January 2000 (five buoys), here we have an additional buoy SW6 for WAM validations. The comparison statistics for April 2000 is as shown in (Table 2). In the Arabian Sea, the WAM hindcasts and the measurements of buoys (DS1, DS2, SW1 and SW4) show correlation coefficients of the order 0.63 to 0.96 for Hs, while in the Bay of Bengal it ranged from 0.66 to 0.89. SI is observed to be low in all cases indicating a better fit between measured and model Hs. Bias is negative for DS1, SW1, SW4 and SW6 which is negligible compared to the higher values of R. Positive bias is observed for DS2 (0.26) and SW5 (0.23) which signifies model computed Hs are slightly higher compared to buoy observations. The PE for Hs is almost higher in most cases. The MPI was noted to be equally strong in both Arabian Sea and Bay of Bengal.
| 2.1. Significant wave height (Hs in m) | |||||||
|---|---|---|---|---|---|---|---|
| Sl. No. | Statistical estimates | Arabian Sea | Bay of Bengal | ||||
| DS1 | DS2 | SW1 | SW4 | SW5 | SW6 | ||
| 1. | Mean (Buoy) | 0.9 | 1.1 | 0.5 | 0.8 | 1.0 | 0.9 |
| 2. | Range (Buoy) | 0.6 – 1.5 | 0.9 – 1.5 | 0.3 – 1.1 | 0.5 – 1.2 | 0.5 – 1.4 | 0.5 – 2.2 |
| 3. | Mean (WAM) | 1.1 | 0.9 | 0.7 | 0.9 | 0.7 | 1.0 |
| 4. | Range (WAM) | 0.6 – 1.6 | 0.7 – 1.1 | 0.4 – 1.2 | 0.5 – 1.3 | 0.5 – 1.1 | 0.5 – 1.4 |
| 5. | R | 0.63 | 0.96 | 0.78 | 0.76 | 0.89 | 0.66 |
| 6. | SI | 0.10 | 0.06 | 0.11 | 0.04 | 0.07 | 0.04 |
| 7. | B | -0.23 | 0.26 | -0.21 | -0.12 | 0.23 | -0.03 |
| 8. | RMSE | 0.09 | 0.07 | 0.06 | 0.04 | 0.07 | 0.03 |
| 9. | PE | 22.2 | 30.2 | 28.7 | 17.3 | 31.9 | 17.7 |
| 10. | MPI | 0.90 | 0.94 | 0.89 | 0.96 | 0.93 | 0.96 |
| 2.2. Mean wave period (Tc in s) | |||||||
| 1. | Mean (Buoy) | 5.2 | 5.0 | 5.3 | 4.4 | 5.4 | 4.2 |
| 2. | Range (Buoy) | 3.9 – 9.4 | 4.2 – 6.7 | 3.0 – 8.9 | 3.4 – 6.6 | 3.9 – 8.6 | 3.1 – 6.4 |
| 3. | Mean (WAM) | 6.5 | 5.6 | 6.5 | 6.4 | 6.0 | 5.4 |
| 4. | Range (WAM) | 4.4 – 9.7 | 4.2 – 8.2 | 3.9 – 9.2 | 4.1 – 8.5 | 4.4 – 9.1 | 3.8 – 6.7 |
| 5. | R | 0.65 | 0.89 | 0.71 | 0.32 | 0.68 | 0.20 |
| 6. | SI | 0.46 | 0.17 | 0.50 | 1.17 | 0.32 | 0.48 |
| 7. | B | -1.25 | -0.59 | -1.24 | -2.30 | -0.59 | -1.16 |
| 8. | RMSE | 2.41 | 0.87 | 2.64 | 5.18 | 1.77 | 2.01 |
| 9. | PE | 19.9 | 9.8 | 20.6 | 30.6 | 16.4 | 22.6 |
| 10. | MPI | 0.54 | 0.83 | 0.50 | 0.27 | 0.68 | 0.52 |
R: Correlation Coefficient, SI: Scatter Index, B: Bias, RMSE: Root Mean Square Error,
PE: Percentage Error & MPI: Model Performance Index.
Table 2: Statistics of the comparison of WAM model wave parameters with NIOT buoy measurements in the Arabian Sea and Bay of Bengal during April 2000 using ERA- 40 winds as shown in figure 13.
The Tc shows reasonably good correlations in the Arabian Sea (0.65 to 0.89), except in one case, 0.32 for SW4 which is quite low. It also shows very poor correlation of 0.20 for SW6 location in the Bay of Bengal and at the same time it shows a fairly good correlation of 0.68 for SW5 in Bay of Bengal. The low correlation coefficient in few cases can be assigned to the fair weather season, which experiences low wind conditions. Bias is negative throughout which are negligible. RMSE varied from 0.87 to 5.18, which indicates high values showing large deviations. The PE is less for DS2 (9.8%), while higher for all other buoys considered. The lower performance of the model is mainly due to the low winds during the fair weather season and also attributed to the poor quality of the input winds.
(Figure 14) shows the comparison between the observed and predicted wave parameters (Hs and Tc) at 6 hourly intervals for the period 01-31 July 2000. The WAM model outputs are validated for seven buoy locations such as DS1, DS2, SW1, SW4, DS3, SW5 and SW6. (Table 3) shows the comparison statistics for July 2000. The model predicted parameters as shown in (Figure 14) shows reasonably strong correlation with the observations for the mean Hs and Ts ranges of 0.9 to 3.3 m and 5.1 to 6.8s respectively during July 2000. In the Arabian Sea and Bay of Bengal, the buoys shows very strong correlation of the order 0.93 to 0.99 for Hs. SI values are noted to be lower indicating better fit between the model and buoy Hs. Bias is positive (DS1, DS2, SW1, SW4, DS3) and negative for SW5 (-0.01) and SW6 (-0.19). Remya et al., [43] have reported similar studies for Indian Ocean region in which the Bay of Bengal statistics shows a very good agreement with buoy data especially in the case of Hs with a low RMSE of 0.29 m, high correlation of 0.91 and a very small bias of -0.04 m. PE is lower in all cases (<10%) except in one case SW6, where it is 18.3%. The MPI in the Arabian Sea and Bay of Bengal is strong enough. Here it may be noted that, the results of MIKE 21 SW (WAM physics) hindcast in the Indian Ocean for the year 2005 using QuickSCAT blended ECMWF winds revealed that the model performance was satisfactory with reasonable confidence [43].
| 3.1. Significant wave height (Hs in m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sl. No. | Statistical estimates | Arabian Sea | Bay of Bengal | ||||||
| DS1 | DS2 | SW1 | SW4 | DS3 | SW5 | SW6 | |||
| 1. | Mean (Buoy) | 3.3 | 2.3 | 1.3 | 2.0 | 2.3 | 1.2 | 0.9 | |
| 2. | Range (Buoy) | 1.8 – 5.5 | 1.2 – 3.7 | 0.7 – 2.1 | 1.1 – 3.3 | 1.2 – 3.5 | 0.7 – 2.0 | 0.4 – 1.4 | |
| 3. | Mean (WAM) | 3.0 | 2.1 | 1.2 | 1.8 | 2.2 | 1.2 | 1.1 | |
| 4. | Range (WAM) | 1.8 – 4.5 | 1.3 – 3.2 | 0.8 – 1.8 | 1.1 – 2.9 | 1.4 – 3.0 | 0.8 – 1.8 | 0.6 – 1.4 | |
| 5. | R | 0.98 | 0.99 | 0.97 | 0.99 | 0.95 | 0.98 | 0.93 | |
| 6. | SI | 0.06 | 0.02 | 0.02 | 0.03 | 0.03 | 0.01 | 0.05 | |
| 7. | B | 0.30 | 0.14 | 0.08 | 0.19 | 0.11 | -0.01 | -0.19 | |
| 8. | RMSE | 0.19 | 0.04 | 0.02 | 0.06 | 0.06 | 0.01 | 0.04 | |
| 9. | PE | 9.5 | 6.3 | 9.1 | 9.1 | 8.7 | 3.8 | 18.3 | |
| 10. | MPI | 0.94 | 0.99 | 0.98 | 0.97 | 0.96 | 0.98 | 0.95 | |
| 3.2. Mean wave period (Tc in s) | |||||||||
| 1. | Mean (Buoy) | 6.8 | 6.3 | 5.8 | 6.5 | 6.3 | 5.5 | 5.1 | |
| 2. | Range (Buoy) | 5.5 – 8.3 | 5.0 – 8.0 | 3.6 – 8.3 | 5.0 – 7.8 | 5.1 – 8.1 | 3.7 – 9.4 | 3.4 – 6.4 | |
| 3. | Mean (WAM) | 6.5 | 6.2 | 5.5 | 6.2 | 6.2 | 5.8 | 5.4 | |
| 4. | Range (WAM) | 5.7 – 7.6 | 5.3 – 7.4 | 3.9 – 7.3 | 5.0 – 7.1 | 5.3 – 8.0 | 3.9 – 8.5 | 4.1 – 6.6 | |
| 5. | R | 0.98 | 0.94 | 0.97 | 0.88 | 0.95 | 0.96 | 0.93 | |
| 6. | SI | 0.02 | 0.02 | 0.03 | 0.03 | 0.01 | 0.04 | 0.03 | |
| 7. | B | 0.26 | 0.08 | 0.23 | 0.24 | 0.10 | -0.25 | -0.30 | |
| 8. | RMSE | 0.14 | 0.12 | 0.16 | 0.18 | 0.08 | 0.22 | 0.15 | |
| 9. | PE | 4.5 | 4.8 | 5.2 | 5.8 | 3.9 | 6.5 | 6.2 | |
| 10. | MPI | 0.99 | 0.98 | 0.96 | 0.97 | 0.99 | 0.96 | 0.97 | |
R: Correlation Coefficient, SI: Scatter Index, B: Bias, RMSE: Root Mean Square Error,
PE: Percentage Error & MPI: Model Performance Index.
Table 3: Statistics of the comparison of WAM model wave parameters with NIOT buoy measurements in the Arabian Sea and Bay of Bengal during July 2000 using ERA- 40 winds as shown in figure 14.
Tc shows strong correlations in the Arabian Sea and Bay of Bengal. SI shows a better fit with lower values. The values of Bias are positive for most buoys considered while it is negative for SW5 (-0.25) and SW6 (-0.30). The PE is less than 7%, which shows the best performance of the model. MPI is also very high indicating strong agreement between the model and measured Tc. It may be noted here that, in case of SW6, the hindcast Tc fits well (6.2%) compared with hindcast Hs (WAM over predicts by 18.3%).
(Figure 15) shows the comparison between observed and predicted wave parameters (Hs and Tc) at 6 hourly intervals for the period 01-31 October 2000. Here, the WAM model outputs are validated for eight buoy locations say DS1, DS2, SW1, SW4, DS3, DS4, SW5 and SW6. On 25th October 2000 a tropical depression developed in central Bay of Bengal and dissipated on 28th whose effect was observed by DS3 and DS4 buoys (Figure 2d). The statistics of the validation of WAM model outputs is as shown in (Table 4). The model predicted parameters as shown in (Figure 15) reveal good match with the observations as reported by several other researchers such as Raj Kumar et al. [13] and Sannasiraj et al. [45] in the Indian Ocean. Studies by Raj Kumar et al. [13], revealed the model performance to be reasonable during high sea state caused by cyclonic disturbance in the Arabian Sea. The difference in hindcast and observed Hs mean for October 2000 and the range of Hs for all the buoy locations considered are well within 0.1 m and 0.4 m respectively being the post-monsoon month. It may be noted from earlier discussion that the range of Hs variability over the Arabian Sea for a typical day, 25 October 2000, 1200 hrs as shown in (Figure 8) was marginal (from 1.4 to 1.8 m). However, higher spatial variability was observed on the same day in the Bay of Bengal, where the prevailing winds were generally variable (Figure 2d). In such a scenario, the buoys (DS1, DS2, SW1 and SW4) in the Arabian Sea shows considerably good correlations of the order 0.76 to 0.94, while in the Bay of Bengal in spite of variable winds and hindcast Hs in terms of its range (spatial variability), DS3, DS4, SW5 and SW6 shows still higher correlations in the range 0.94 to 0.97 for Hs. SI and RMSE are noted to be lower during this period. The PE estimates is less than 15% and the the values of MPI are high enough (near to 1.0) for all the buoys considered. A typical case of severe cyclonic system named Phailin reported a maximum wave height of 13.5 m off Gopalpur, northeast coast of India [46]. The wave forecast results of INCOIS using MIKE SW model (WAM physics) compared well with the buoy measurements (BD08, BD11, BD14 and DWR) with correlation coefficient ranging from 0.88 to 0.98 for Hs range of 1.0 to 7.3 m. The higher deviations for Hs during the month of Oct 2000 may be partially attributed to the forcing wind field. Apart from that, since it is a fair weather season, the study area would be dominated by long swells and the representation of swell propagation in model physics in the model could be the reason for this deviation.
| 4.1. Significant wave height (Hs in m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sl. No. | Statistical estimates | Arabian Sea | Bay of Bengal | ||||||
| DS1 | DS2 | SW1 | SW4 | DS3 | DS4 | SW5 | SW6 | ||
| 1. | Mean (Buoy) | 1.2 | 1.3 | 0.7 | 0.8 | 1.8 | 1.3 | 1.0 | 0.8 |
| 2. | Range (Buoy) | 0.8 – 1.9 | 0.7 – 2.2 | 0.2 – 1.2 | 0.5 – 1.5 | 0.5 – 3.0 | 0.9 – 2.6 | 0.5 – 1.8 | 0.5 – 1.8 |
| 3. | Mean (WAM) | 1.1 | 1.2 | 0.6 | 0.9 | 1.6 | 1.2 | 1.1 | 0.9 |
| 4. | Range (WAM) | 0.8 – 1.6 | 0.9 – 1.8 | 0.3 – 0.9 | 0.6 – 1.2 | 0.5 – 2.6 | 0.7 – 2.2 | 0.7 – 1.7 | 0.5 – 1.6 |
| 5. | R | 0.76 | 0.94 | 0.92 | 0.87 | 0.97 | 0.96 | 0.94 | 0.96 |
| 6. | SI | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 |
| 7. | B | 0.01 | -0.03 | -0.01 | -0.04 | 0.14 | 0.11 | -0.01 | -0.03 |
| 8. | RMSE | 0.02 | 0.02 | 0.01 | 0.02 | 0.04 | 0.03 | 0.01 | 0.01 |
| 9. | PE | 9.3 | 9.6 | 14.5 | 12.1 | 10.5 | 10.8 | 7.8 | 8.6 |
| 10. | MPI | 0.99 | 0.98 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | 0.98 |
| 4.2. Mean wave period (Tc in s) | |||||||||
| 1. | Mean (Buoy) | 5.7 | 5.9 | 6.4 | 5.2 | 6.8 | 7.2 | 5.6 | 5.9 |
| 2. | Range (Buoy) | 4.4 – 9.2 | 4.5 – 8.6 | 3.7 – 10.5 | 3.9 – 7.0 | 4.8 – 9.1 | 4.4 – 11.7 | 3.7 – 8.7 | 3.6 – 7.3 |
| 3. | Mean (WAM) | 6.5 | 6.7 | 6.9 | 6.2 | 7.0 | 7.7 | 6.2 | 6.3 |
| 4. | Range (WAM) | 4.7 – 9.6 | 4.4 – 9.2 | 3.8 – 10.5 | 4.0 – 7.9 | 5.1 – 9.0 | 5.3 – 11.8 | 4.3 – 9.1 | 4.1 – 8.0 |
| 5. | R | 0.82 | 0.80 | 0.89 | 0.82 | 0.81 | 0.88 | 0.90 | 0.88 |
| 6. | SI | 0.20 | 0.14 | 0.13 | 0.26 | 0.06 | 0.15 | 0.11 | 0.08 |
| 7. | B | -0.82 | -0.74 | -0.49 | -1.03 | -0.20 | -0.49 | -0.62 | -0.48 |
| 8. | RMSE | 1.13 | 0.85 | 0.81 | 1.36 | 0.39 | 1.06 | 0.63 | 0.46 |
| 9. | PE | 15.1 | 12.8 | 11.8 | 17.1 | 7.4 | 12.2 | 11.0 | 8.4 |
| 10. | MPI | 0.80 | 0.86 | 0.87 | 0.74 | 0.94 | 0.85 | 0.89 | 0.92 |
R: Correlation Coefficient, SI: Scatter Index, B: Bias, RMSE: Root Mean Square Error,
PE: Percentage Error & MPI: Model Performance Index.
Table 4: Statistics of the comparison of WAM model wave parameters with NIOT buoy measurements in the Arabian Sea and Bay of Bengal during October 2000 using ERA-40 winds as shown in figure 15.
The Tc also show reasonably good correlations for all buoys located in the Arabian Sea and Bay of Bengal. SI is low in all cases considered and Bias is negative throughout. The high values of MPI and lower values of PE (<17%) clearly indicates that the model could reasonably reproduce the wave periods at the buoy locations.
(Figure 16) shows the comparison between the buoy OB10 and predicted wave parameters (Hs and Tc) at 6 hourly intervals for the period 01-31 January 2009. (Table 5) shows the statistics of the validation of WAM model outputs for January 2009. The model predicted parameters as shown in (Figure 16) shows strong correlation with the observations. The estimated means and ranges of Hs for the buoy and WAM hindcasts deviate by 0.1 and 0.2 m respectively (January 2009). The buoy and hindcast Hs show a correlation coefficient of 0.97 and a SI of 0.02. Estimated Bias and RMSE are -0.01 m and 0.02 respectively, which reveal a good agreement between the model and observations with PE of 11.1%. The MPI is high enough (0.98) indicating that the model could simulate Hs very well at OB10 location. Similar comparison is made between buoy (OB10) data and model (MIKE 21 SW) derived wave heights at one buoy location in Bay of Bengal (OB10) for October 2008 to August 2009 by Sabique et al. [47]. The comparisons show that the model derived wave parameters agree well with the observed wave parameters. The statistics revealed a good correlation with coefficient R (0.93), RMSE (0.30), Bias (0.11) and SI (0.19) for Hs. Tc also shows reasonably a good correlation (R=0.85) between buoy and WAM hindcast. The mean of Tc for the buoy and WAM hindcast deviated by 0.4s for the observed/predicted range of 3.9 to 8.9s. The SI of 0.11 indicates a good fit between the observed Tc and WAM hindcast. Hindcast Tc shows a considerable bias of -0.49. The values of RMSE, PE and MPI are 0.56, 8.7 and 0.89 respectively. All of them (estimated statistics) reveal very good agreement between the models and buoy (OB10) observations excepting for few observations as seen from (Figure 16) In another similar study carried out earlier, Tc comparisons by Sabique et al. [47], at a buoy location in the Bay of Bengal (OB10) gave a correlation of 0.67, RMSE (1.2), Bias (-0.81) and SI (0.21).
| 5.1. Significant wave height (Hs in m) | ||
|---|---|---|
| Sl. No. | Statistical estimates | Bay of Bengal |
| OB10 | ||
| 1. | Mean (Buoy) | 1.1 |
| 2. | Range (Buoy) | 0.4 – 2.1 |
| 3. | Mean (WAM) | 1.0 |
| 4. | Range(WAM) | 0.6 – 1.9 |
| 5. | R | 0.97 |
| 6. | SI | 0.02 |
| 7. | B | -0.01 |
| 8. | RMSE | 0.02 |
| 9. | PE | 11.1 |
| 10. | MPI | 0.98 |
| 5.2. Mean wave period (Tc in s) | ||
| 1. | Mean (Buoy) | 5.1 |
| 2. | Range (Buoy) | 3.9 – 8.4 |
| 3. | Mean (WAM) | 5.5 |
| 4. | Range (WAM) | 4.3 – 8.9 |
| 5. | R | 0.85 |
| 6. | SI | 0.11 |
| 7. | B | -0.49 |
| 8. | RMSE | 0.56 |
| 9. | PE | 8.7 |
| 10. | MPI | 0.89 |
R: Correlation Coefficient, SI: Scatter Index, B: Bias,
RMSE: Root Mean Square Error, PE: Percentage Error &
MPI: Model Performance Index.
Table 5: Statistics of the comparison of WAM model wave parameters with buoy measurements in the Bay of Bengal during January 2009 as shown in figure 16.
Hence, overall the validation and performance assessment were promising though significant departures were noted. Low wave heights are not estimated properly in WAM. This may be attributed to simplifications like the neglect of atmospheric stratification effects when converting wind speeds to the wind stress fields driving WAM. Larger deviation in Hs is observed at locations DS1, SW1, SW4 and SW6. It is well known that, WAM is a deep water model capable of simulating waves accurately up to 30 m water depth since they include crude shallow water equations, which does not satisfy near-shore wave transformations. However, in this study the deep water hindcasts have been compared with the buoy observations at 16 to 24 m in the absence of measurements at preferable locations where water depth is more than 30 m. It was seen in most cases the PE values around 20% excepting in few cases where it was higher. Therefore, by considering the buoy data from such locations bordering 30 m of water depth were found to be useful to assess and evaluate the extent of agreement between the models (PE around 20%) and buoy at deeper than 15 m, which is the limiting depth for near-shore wave transformations.
Sensitivity of the model to two different wind forcings
The study also investigated the sensitivity of the model to two different wind products such as ERA-40 and QuikSCAT NCEP blended winds. It is noted that in the validation study for the selected months – January, April, July and October 2000 using ERA-40 winds (Figures 12-15) the model showed significant underestimation and over estimation of Hs and Tc at many buoy locations considered in the Arabian Sea and Bay of Bengal. The inaccuracy in the input wind fields could be a possible reason for the mismatch at the buoy locations. Hence, an attempt was made to study the response of the model to two different wind field product such as ERA-40 and blended winds for selected buoys in the Arabian Sea and Bay of Bengal. In specific, apart from ERA-40 winds the QuikSCAT-NCEP Blended winds were used to force the wave model. Here, the WAM model outputs are validated for three buoy locations say DS1 (off Goa), and DS2 (off Lakshadweep) in the Arabian Sea and SW6 (off Chennai port).
(Figure 17) presents the comparison between the observed (buoys) and predicted wave parameters (Hs and Tc) at 6 hourly intervals for selected buoys in the Indian Seas (January, April, July & October 2000) using two different wind fields (ERA-40 and QuikSCAT/NCEP Blended winds). In the (Figure 17), WAM (ERA) and WAM (QNB) denotes the wave simulations using ERA-40 and QuikSCAT-NCEP blended winds respectively. The statistics of the comparison of the sensitivity of the model to two different wind fields is as shown in (Table 6). From the analysis, it is evident that WAM model using blended winds could reproduce the Hs and Tc at the buoy locations with appreciable accuracy compared with the validation results using ERA-40 winds. In all the cases considered, R>0.9 for Hs and Tc using blended winds. During 1 – 30 January 2000 at the DS2 location, the PE reduced from 18.7 to 4.3% and 14.9 to 2.1% for Hs and Tc respectively. Similarly, during April 2000, there is a notable reduction in the PE (22.2 to 5.1%) using blended winds in comparison with ERA-40 winds. Another notable feature is the favorably good performance of the model at SW6 buoy location during July 2000 where with the application of blended winds the model demonstrated a significant reduction in PE for Hs from 18.3 to 5.5% with lower bias compared to ERA-40 winds. During the months of January, April and July 2000, significant over estimation of Hs using ERA-40 winds is noted at the DS2, DS1 and SW6 locations. However, with the use of blended winds the WAM model could reproduce the Hs with good accuracy at these locations with reduced bias and low PE (<6%). Similarly, over estimation of Tc during January, April and October 2000 is highly reduced at the buoy locations DS1 and DS2 with notably low bias and low PE (<4%). It is inferred from (Table 6) that the model-derived Hs and Tc with forcing from blended winds agree well with observed wave data and exhibit better statistical estimates compared with the simulation results using ERA-40 winds for the period of study. Qualitatively, the model output obtained here are reasonably consistent with those obtained at the buoy location.
| 6.1. Significant wave height (Hs in m) WAM (ERA) / WAM (QNB) |
||||||
|---|---|---|---|---|---|---|
| Sl. No. | Statistical Estimates | January 2000 | April 2000 | July 2000 | October 2000 | |
| DS2 | DS1 | DS1 | SW6 | DS1 | ||
| 1. | R | 0.86/ 0.97 | 0.63/ 0.95 | 0.98/ 0.99 | 0.93/ 0.98 | 0.76/ 0.95 |
| 2. | B | -0.18/ 0.09 | -0.23/ 0.11 | 0.30/ 0.09 | -0.19/ 0.11 | 0.01/ 0.007 |
| 3. | PE | 18.7/ 4.3 | 22.2/ 5.1 | 9.5/ 2.4 | 18.3/ 5.5 | 9.3/ 4.9 |
| 6.2. Mean wave period (Tc in s) WAM (ERA) / WAM (QNB) |
||||||
| 1. | R | 0.70/ 0.98 | 0.65/ 0.97 | 0.98/ 0.99 | 0.93/ 0.98 | 0.82/ 0.98 |
| 2. | B | -0.89/ 0.05 | -1.25/ 0.02 | 0.26/ 0.07 | -0.30/ 0.04 | -0.82/ 0.08 |
| 3. | PE | 14.9/ 2.1 | 19.9/ 1.8 | 4.5/ 1.3 | 6.2/ 2.6 | 15.1/ 3.2 |
R: Correlation Coefficient, B: Bias and PE: Percentage Error
Table 6: Statistics of the comparison of WAM model wave parameters with buoy measurements in the Arabian Sea and Bay of Bengal using ERA-40 winds and QuikSCATNCEP blended winds as shown in figure 17.
The overall evaluation based on statistical measures using two different wind forcings show that model performs well during all periods (January, April, July and October 2000) using blended winds. One important feature from the comparison of wave hindcasts using blended winds is that, the model could reasonably simulate the Hs and Tc at the shallow water buoy (SW6) location with better accuracy. The quality of the blended winds has a significant impact in simulating the wave fields realistically, at the buoy locations considered. At the same time, the comparisons using ECMWF winds gave a moderate performance. Most importantly, during the fair-weather season, the study area would be dominated by long swells and the representation of swell propagation in model physics could be a possible reason. Hence, it can be concluded that apart from wind forcing wave model physics, numeric and model grid resolution are major factors, which affect the model performance. These studies indicate that use of higher-frequency winds to force the wave model yields positive output impact, particularly in the sense of significant wave height. In short, without high quality wind forcing fields, wave model results may suffer even given the correct physics. Furthermore, one can speculate that the quality of wind forcing fields becomes even more critical when considering higher-order wave spectral moments because these terms are more directly associated with shorter waves and hence tied more strongly to the wind forcing.
The third generation wave model (WAM Cycle 4.5.3) simulations have been carried out for the North Indian Ocean from 50°E to 100°E and 0°N to 30°N using the analysed winds such as ERA-40 and QuikSCAT/ NCEP Blended wind fields and boundary conditions generated from 1° × 1° global runs. The model outputs such as significant wave height and mean wave period are compared with the buoy measurements. The validation of WAM with NIOT buoys, irrespective of the input winds used was quite promising for the North Indian Ocean with Model Performance Index ranging from 0.92 to 0.99 and Percentage Error ranging from 3.0 to 19.7% in most cases for January, June/July and October excepting April. Comparison between the predicted and observed wave parameters are very encouraging, excepting the higher model estimates of significant wave height and the mismatch in lower wave heights at few buoy locations. During the month of April, winds are generally found to be low and variable, which are not accurately reproduced in the input winds so far, as in the present study. This is the most likely reason for higher discrepancies between the wave model and the measurements in April, pre-monsoon period. Further the sensitivity of the model to two different wind forcings was analyzed and it was concluded that blended winds could accurately reproduce Hs and Tc at the buoy locations with low statistical errors. With the application of blended winds WAM model simulated Hs and Tc revealed PE < 6 % and < 4 % respectively with low bias and R > 0.9 compared with ERA-40 winds for all buoys considered. The results of the study has demonstrated the sensitivity of WAM model to the quality of wind forcing, such that the quality of the wind fields is reflected in the quality of the wave predictions. Hence, the present study suggests that, WAM Cycle 4.5.3 wave model predictions are reliable for the Indian Seas using the analysed wind fields such as ERA-40 and QuikSCAT/NCEP Blended wind fields with notably better performances using blended wind fields. The study further suggest for extensive validations using buoy measurements leading to a development of a long-term hindcast database for the North Indian Ocean, which has potential applications for meteorologists, oceanographers, coastal engineers and operational forecasters.
The authors express their sincere thanks to Director, NPOL; Director, SAC and Group Head, Ocean Sciences for their encouragement and support provided to carry out this work. This is a part of the Ph.D. work of Umesh P. A., carried out under a collaborative project between NPOL and SAC, Ahmedabad (Project: NPOL/SAC-II) at Naval Physical and Oceanographic Laboratory, DRDO, Cochin. They are extremely thankful to fellow scientists of Data Management Division, Ocean Science Group, NPOL for their timely support and encouragement. They are also grateful to Director, NIOT (National Institute of Technology, Chennai) and Director, INCOIS (Indian National Centre for Ocean Information Services, Hyderabad) who have provided wave data for this study.